7.1.4 纳什均衡的计算复杂性
近年来,理论计算机科学家对有限策略型博弈的(混合策略)纳什均衡计算复杂性问题产生了极大关注。根据纳什定理,我们已经知道有限策略型博弈肯定存在至少一个纳什均衡。因此,寻找纳什均衡问题属于总搜寻问题范畴,即在这类问题中,解一定存在,研究者的目标是找到解。
首先,我们介绍两个重要的总搜寻问题(total search problem):纳什问题(NASH):给定一个策略型博弈,找出其混合策略纳什
均衡。混合策略纳什均衡解可能有多个,但只需找到一个即可。
布劳威尔问题(BROUWER):给定集合[0,1]𝑚(这是一个紧且凸的集合)上的连续函数𝑓,找到函𝑓的不动点,即找到[0,1]𝑚中的点𝑥,使得𝑓(𝑥) = 𝑥。注意,这里的𝑚是一个有限正整数,而且函数𝑓可能有多个不动点,但我们只要找到一个即可。
计算机学家 Papadimitriou 提出了 TFNP 这一复杂类[11] ,用于描述所有满足以下条件的搜寻问题:每个问题实例都有解。换句话说,对于给定的搜寻问题,如果其每个实例都有解,则属于 TFNP 类。例如,FACTOR(分解质因数)问题将整数作为输入,确定其所有质因数。纳什问题也是一个相关例子:找到有限策略型博弈的确切纳什均衡或𝜀-近似纳什均衡。
Papadimitriou 还根据证明总搜寻问题每个实例都有解的过程中
所用的"论据"(arguments)将总搜寻问题进行了分类。这些论据在证明问题解存在性时起到了非构建性的步骤角色。基于这一分类标准,他将总搜寻问题分为以下几类:
PPA(多项式奇偶性论据):如果给定的图有一个奇数度(odd degree)节点,那么它必定至少有另外一个奇数度节点。这被称为奇偶性论据(parity argument,PA)。如果一个问题能够在多项式时间内归约为如下问题:在能以多项式规模表示的图中寻找含有一个奇数度节点的环路(polynomial sized circuit),则此问题属于 PPA 类。
PPAD(有向图的多项式奇偶性论据):给定一个有向图,任一节点的出度是它的传出弧的个数,入度是它的传入弧的个数。如果节点的入度不等于出度,那么该节点是不平衡的。PPAD 论据表明,如果有向图有一个不平衡节点,那么它必定至少存在着另外一个不平衡节点。
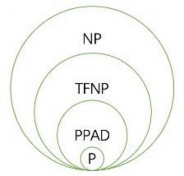
图 1-1 展示了各类总搜寻问题之间的关系(该图假设P ⊈ NP。若 P = NP,则所有类别都合并为一类)。

图 1-1 不同复杂类之间的关系
PPAD 中的问题确实非常困难,这是一个引人入胜的研究领域。如果P=NP,那么 PPAD 问题将被解决,因为此时 PPAD 将等同于P。然而,几十年来,理论计算机科学家一直在尝试为 PPAD 中的一些问题(如布劳威尔问题、纳什问题、EOL 问题等)设计高效的算法,但
却未能成功。因此,除非 P=NP 成立,我们无法确定 PPAD 是否包含难解问题。
LemkeHowson 算法提供了二人博弈纳什均衡存在的另一种证明方法。基于这一观察,我们可以定义如下问题,称之为"EndofALine"
(EOL)问题。
𝑆, 𝑃: {0,1}𝑛 → {0,1}𝑛,并且满足𝑃(0𝑛) = 𝑆(0𝑛) = 0𝑛。该问题的输出是一个向量𝑥 ∈ {0,1}𝑛,使得𝑆(𝑃(𝑥)) ≠ 𝑥 ≠ 0或者𝑃(𝑆(𝑥)) ≠ 𝑥。
EOL 问题是下列总搜寻问题的一个特殊情形:给定一个有向图𝐺以及已指定的不平衡节点,要找到𝐺的另外一个不平衡节点。在 EOL问题中,我们假设𝐺的每个节点至多有一条传入边和至多有一条传出边。在这种限制下,给定的图必定是一组路径和环路。图 1-2 提供了一些具有代表性的这种图形的示例。
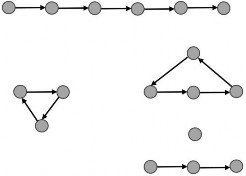
图 1-2 EOL 问题的一些例子
理论计算机学者已经证明 EOL 问题是 PPAD-complete 的。基于这一事实,我们可以立即得到以下两个结果:
若 EOL 问题可以归约为问题𝑋,则问题𝑋是 PPAD-complete 的。若问题𝑌可以归约为 EOL 问题,则问题𝑌属于 PPAD 类。
定理 13 纳什问题是 PPAD-complete 问题。
证明:首先,我们证明纳什问题属于 PPAD 类,方法是将纳什问
题归约为 EOL 问题。
其次,我们证明纳什问题是 PPAD-complete 问题,方法是将 EOL
问题归约为纳什问题。
在上述两个方向的证明中,布劳威尔问题发挥了关键作用。 ∎
由于纳什问题是 PPAD-complete 问题,在理论分析的基础上,学 者们开始寻找新的求解纳什均衡的方法。得益于计算机算力的提高和 人工智能算法的发展,逐渐涌现出一些使用人工智能算法求解纳什均 衡的算法。在计算纳什均衡时,深度学习和强化学习可以起到关键的 作用。首先,深度学习可以用于特征提取。在纳什均衡计算中,每个 玩家的策略都是一个向量,向量的每个元素代表了一种策略。深度学 习可以通过学习大量的样本数据,提取出每个玩家的策略特征,从而 减少计算量,提高计算效率。其次,深度学习也可以用于策略预测。在纳什均衡计算中,每个玩家的策略都是基于其他玩家的策略制定的。深度学习可以通过学习大量的样本数据,预测每个玩家的策略,从而 为纳什均衡的计算提供基础。另一方面,强化学习可以用于策略优化。在纳什均衡计算中,每个玩家的策略都需要不断优化,以应对其他玩 家的策略变化。强化学习可以通过与环境交互,学习最优的策略组合,从而优化纳什均衡的计算结果。总之,深度学习和强化学习在计算纳 什均衡时都具有重要的应用价值。它们可以帮助我们提高计算效率,预测策略,优化结果,从而更好地解决纳什均衡问题。同时,这些算 法的应用也受到了一些限制,例如它们需要大量的数据和计算资源,而且它们可能无法处理一些非常复杂的问题。因此,在未来,我们需 要进一步研究这些算法,以提高它们的性能和效率,从而更好地解决 纳什均衡问题。例如,多智能体强化学习研究如何利用多个智能体之 间通信、协作的方法共同完成一个任务。这一方向十分适合应用在求 解多人纳什均衡以及合作博弈均衡上。