2.2 多维随机变量（随机向量）

2.2 多维随机变量 (随机向量)

0.1. 1 离散型随机向五的分布

随机向量的概念在 2.1 节 2.1.1 段中已提及过了.一般,设 \(X\) \(=\left(X_{1}, X_{2}, \cdots, X_{n}\right)\) 为一 \(n\) 维向量, 其每个分量, 即 \(X_{1}, \cdots, X_{n}\), 都 是一维随机变量,则称 \(X\) 是一个 \(n\) 维随机向量或 \(n\) 维随机变量.

与随机变量一样, 随机向量也有离散型和连续型之分. 本段先 考虑前者, 一个随机向量 \(X=\left(X_{1}, \cdots, X_{n}\right)\), 如果其每一个分量 \(X_{i}\) 都是一维离散型随机变量,则称 \(X\) 为离散型的.

定义 2.1 以 \(\left\{a_{i 1}, a_{i 2}, \cdots\right\}\) 记 \(X_{i}\) 的全部可能值, \(i=1,2, \cdots\), 则事件 \(\left\{X_{1}=a_{1_{j_{1}}}, X_{2}=a_{2_{j_{2}}} \cdots, X_{n}=a_{n_{j_{n}}}\right\}\) 的概率

\[ \begin{gathered} p\left(j_{1}, j_{2}, \cdots, j_{n}\right)=P\left(X_{1}=a_{1 j_{1}}, X_{2}=a_{2 j_{2}}, \cdots, X_{n}=a_{n j_{n}}\right) \\ j_{1}=1,2, \cdots, j_{2}=1,2, \cdots, \cdots, j_{n}=1,2, \cdots \end{gathered} \]

称为随机向量 \(X=\left(X_{1}, \cdots, X_{n}\right)\) 的概率函数或概率分布, 概率函 数应满足条件:

\[ p\left(j_{1}, j_{2}, \cdots, j_{n}\right) \geqslant 0, \sum_{j_{n}} \cdots \sum_{j_{2}} \sum_{j_{1}} p\left(j_{1}, j_{2}, \cdots, j_{n}\right)=1 \]

例 2.1 图 2.5 所示的二维离散型随机向量 \(X=\left(X_{1}, X_{2}\right)\) 的 概率分布为

\[ \begin{aligned} & P\left(X_{1}=2, X_{2}=1\right)=1 / 3 \\ & P\left(X_{1}=2, X_{2}=2.5\right)=1 / 4 \\ & P\left(X_{1}=5, X_{2}=3\right)=5 / 12 \end{aligned} \]

从图上看出, \(X_{1}\) 的可能值为 2 和 \(5, X_{2}\) 的可能值为 \(1,2.5\) 和 3. 故 形式上看, \(X=\left(X_{1}, X_{2}\right)\) 应有 6 组可能值, 即 \((2,1),(2,2.5)\), \((2,3),(5,1),(5,2.5),(5,3) . X\) 的概率分布告诉我们, 实际上只

图 2.5

有第 \(1,2,6\) 组是真正的可能值,但 这并无关系: 对一组不可能的值, 只要把它的概率定为 0 就行了. 这 一做法使我们可以把离散型分布 统一写成 \((2.1)\) 的格式, 在理论上 有其方便之处. 自然, 在具体例子 中,如例 2.1 并无必要硬凑成那个 形式, 只要指出概率大于 0 的那部 分就行了.

例 2.2 多项分布.

多项分布是最重要的离散型多维分布. 设 \(A_{1}, A_{2}, \cdots, A_{n}\) 是 某一试验之下的完备事件群, 即事件 \(A_{1}, \cdots, A_{n}\) 两两互斥, 其和为 必然事件(每次试验时, 事件 \(A_{1}, \cdots, A_{n}\) 必发生一个且只发生一 个). 分别以 \(p_{1}, p_{2}, \cdots, p_{n}\) 记事件 \(A_{1}, A_{2}, \cdots, A_{n}\) 的概率, 则 \(p_{i} \geqslant\) \(0, p_{1}+\cdots+p_{n}=1\).

现在将试验独立地重复 \(N\) 次,而以 \(X_{i}\) 记在这 \(N\) 次试验中事 件 \(A_{i}\) 出现的次数, \(i=1, \cdots, n\), 则 \(X=\left(X_{1}, \cdots, X_{n}\right)\) 为 \(-n\) 维随机 向量. 它取值的范围是: \(X_{1}, \cdots, X_{n}\) 都是非负整数且其和为 \(N . X\) 的概率分布就叫做多项分布, 有时记为 \(M\left(N ; p_{1}, \cdots, p_{n}\right)\). 为定出 这分布,要计算事件

\[ B=\left\{X_{1}=k_{1}, \cdots, X_{i}=k_{i}, \cdots, X_{n}=k_{n}\right\} \]

的概率, 只须考虑 \(k_{i}\) 都是非负整数且 \(k_{1}+\cdots+k_{n}=N\) 的情况, 否 则 \(P(B)=0\). 为计算 \(P(B)\), 从 \(N\) 次试验的原始结果 \(j_{1} j_{2} \cdots j_{N}\) 出 发,它表示第一次实验事件 \(A_{j_{1}}\) 发生,第二次试验 \(A_{j_{2}}\) 发生, 等等. 为使事件 \(B\) 发生, 在 \(j_{1}, j_{2}, \cdots, j_{N}\) 中应有 \(k_{1}\) 个 \(1, k_{2}\) 个 2 , 一等等. 这种序列的数目,等于把 \(N\) 个相异物体分成 \(n\) 堆,各堆依次有 \(k_{1}, k_{2}, \cdots, k_{n}\) 件的不同分法. 据第一章 (2.6) 式,不同分法有 \(N ! /\) \(\left(k_{1} ! \cdots k_{n} !\right)\) 个. 其次, 由于独立性, 利用概率乘法定理知, 每个适 合上述条件的原始结果序列 \(j_{1} j_{2} \cdots j_{n}\) 出现的概率, 应为 \(p_{1^{1}}^{k} p_{2^{2}}^{k} \cdots\) \(p_{n^{n}}^{k}\). 于是得到

\[ P\left(X_{1}=k_{1}, X_{2}=k_{2}, \cdots, X_{n}=k_{n}\right)=\frac{N !}{k_{1} ! k_{2} ! \cdots k_{n} !} p_{1}^{k} p_{2}^{k_{2}} \cdots p_{n^{n}}^{k^{n}} \]

\(\left(k\right.\) 为非负整数, \(k_{1}+\cdots+k_{n}=N\) )

(2.3) 就是多项分布,名称的来由是因多项展开式

\[ \left(x_{1}+\cdots+x_{n}\right)^{N}=\sum^{*} \frac{N !}{k_{1} ! \cdots k_{n} !} x_{1}^{k} \cdots x_{n^{n}}^{k} \]

\(\sum^{*}\) 表示求和的范围为: \(k_{i}\) 为非负整数, \(k_{1}+\cdots+k_{n}=N\), 在 (2.4) 中令 \(x_{i}=p_{i}\) 并利用 \(p_{1}+\cdots+p_{n}=1\), 得

\[ \sum^{*} \frac{N !}{k_{1} ! \cdots k_{n} !} p_{1}^{k} \cdots p_{n^{n}}^{k^{n}}=1 \]

这说明分布 (2.3)适合条件(2.2).

多项分布在实用上颇常见: 当一个体按某种属性分成几类时, 就会涉及这个分布. 例如, 一种产品分成一等品 \(\left(A_{1}\right) 、\) 二等品 \(\left(A_{2}\right)\) 、三等品 \(\left(A_{3}\right)\) 和不合格品 \(\left(A_{4}\right)\) 四类.若生产该产品的某厂, 其一、三、三等品和不合格品的比率分别为 \(0.15,0.70,0.10\) 和 0.05 , 从该厂产品中抽出 \(N\) 个. 若这 \(N\) 个只占其产品的极少一部 分, 则可以把这 \(N\) 个看成一个一个地独立抽出, 且在抽取过程中, 各等品的概率(即比率)不变. 在这种情况下, 若分别以 \(X_{1}, \cdots, X_{4}\) 记这 \(N\) 个产品中一、二、三等和不合格品的个数,则 \(X=\left(X_{1}, \cdots\right.\), \(\left.X_{4}\right)\) 将有多项分布 \(M(N ; 0.15,0.70,0.10,0.05)\). 又如在医学上, 一种疾病的患者可按严重的程度分期等等, 都属于这种情况.

如果 \(n=2\), 即只有 \(A_{1}, A_{2}\) 两种可能, 这时 \(A_{2}\) 就是 \(A_{1}\) 的对 立事件. 由于这时有 \(X_{1}+X_{2}=N, X_{1}\) 唯一地决定了 \(X_{2}\), 我们不必 同时考虑 \(X_{1}\) 和 \(X_{2}\), 而只须考虑 \(X_{1}\) 就够了, 这就回到二项分布的 情形.

0.2. 2 连续型随机向量的分布

设 \(X=\left(X_{1}, \cdots, X_{n}\right)\) 是一个 \(n\) 维随机向量. 其取值可视为 \(n\) 维欧氏空间 \(R^{n}\) 中的一个点. 如果 \(X\) 的全部取值能充满 \(R^{n}\) 中某一 区域,则称它是连续型的.

与一维连续型变量一样, 描述多维随机向量的概率分布, 最方 便的是用概率密度函数. 为此我们引进一个记号: \(X \in A\), 读作 “ \(X\) 属于 \(A\) ”或 “ \(X\) 落在 \(A\) 内”, 其中 \(A\) 是 \(R^{n}\) 中的集合. \(\{X \in A\}\) 是一 个随机事件, 因为作了试验以后, \(X\) 之值就知道了, 因而也就能知 道它是否落在 \(A\) 内.

定义 2.2 若 \(f\left(x_{1}, \cdots, x_{n}\right)\) 是定义在 \(R^{n}\) 上的非负函数, 使对 \(R^{n}\) 中的任何集合 \(A\), 有

\[ P(X \in A)=\int_{A} \cdots \int f\left(x_{1}, \cdots, x_{n}\right) \mathrm{d} x_{1} \cdots \mathrm{d} x_{n} \]

则称 \(f\) 是 \(X\) 的 (概率) 密度函数.

如果把 \(A\) 取成全空间 \(R^{n}\), 则 \(\{X \in A\}\) 为必然事件, 其概率为 1. 因此应有

\[ \int_{-\infty}^{\infty} \cdots \int f\left(x_{1}, \cdots, x_{n}\right) \mathrm{d} x_{1} \cdots \mathrm{d} x_{n}=1 \]

这是一个概率密度函数必须满足的条件.

例 2.3 考虑二维随机向量 \(X=\left(X_{1}, X_{2}\right)\), 其概率密度函数 为

\[ \begin{aligned} & f\left(x_{1}, x_{2}\right) \\ & \quad= \begin{cases}1 /[(b-a)(d-c)], & \text { 当 } a \leqslant x_{1} \leqslant b, c \leqslant x_{2} \leqslant d \\ 0, & \text { 其他处 }\end{cases} \end{aligned} \]

则 \(f\) 非负且条件 (2.6) 满足. 从 \(f\) 的形状看出,它在图 2.6 中那个 矩形之外为 0 , 说明 \(\left(X_{1}, X_{2}\right)\) 只能取该矩形内的点为值. 在这矩形 内, 密度各处一样, 因而全部概率均匀地分布在这矩形内. 从公式 (2.5) 看出: 若集 \(A\) 在矩形内, 则 “ \(X\) 落在 \(A\) 内” 的概率 \(P(X \in A)\), 与 \(A\) 的面积成正比而与其位置及形状无关, 这是均匀 性的另一种说法. 以此之故, 人们把本例中 \(X\) 的分布称为上述矩 形上的均匀分布.

例 2.4 向一个无限平面靶射击, 设命中点 \(X=\left(X_{1}, X_{2}\right)\) 有

图 2.6

图 2.7

1. 概率密度

\[ f\left(x_{1}, x_{2}\right)=\pi^{-1}\left(1+x_{1}^{2}+x_{2}^{2}\right)^{-2} \]

从这个函数看出: 命中点的密度只与该点与靷心的距离 \(r\) 有关. 这可以解释为: 在图 2.7 中以靷心 \(O\) 为中心的圆周上各点有同等 被命中的机会. 另外, \(x_{1}^{2}+x_{2}^{2}\) 愈小则 \(f\) 愈大, 说明与靶心接近之 点, 较之远离靶心之点, 有更大的命中机会.

为验证 (2.6) 式只须转到极坐标, 得

\[ \begin{aligned} & \iint_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \\ & =\int_{0}^{2 \pi} \mathrm{d} \theta \int_{0}^{\infty} \pi^{-1}\left(1+r^{2}\right)^{-2} r \mathrm{~d} r \\ & =2 \pi \cdot \pi^{-1} \int_{0}^{\infty}(1+t)^{-2} \mathrm{~d} t / 2=1 \end{aligned} \]

而“命中点与靶心之距离不超过 \(r_{0}\) ”这个事件 \(A\) 的概率为

\[ \begin{aligned} & \iint_{x_{1}^{2}+x_{2}^{2} \leqslant r_{0}^{2}} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \\ & \quad=\int_{0}^{2 \pi} \mathrm{d} \theta \int_{0}^{r_{0}} \pi^{-1}\left(1+r^{2}\right)^{-2} r \mathrm{~d} r=r_{0}^{2} /\left(1+r_{0}^{2}\right) \end{aligned} \]

例 2.5 二维正态分布. 最重要的多维连续型分布是多维正态分布. 对二维的情况, 其 概率密度函数有形式

\[ \begin{aligned} f\left(x_{1}, x_{2}\right)= & \left(2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}\right)^{-1} \exp \left(-\frac{1}{2\left(1-\rho^{2}\right)}\left(\frac{\left(x_{1}-a\right)^{2}}{\sigma_{1}^{2}}\right.\right. \\ & \left.\left.-\frac{2 \rho\left(x_{1}-a\right)\left(x_{2}-b\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(x_{2}-b\right)^{2}}{\sigma_{2}^{2}}\right)\right) \end{aligned} \]

这里为书写方便,引进了一个记号 \(\exp\). 其意义是: \(\exp (c)=\mathrm{e}^{c} \cdot f\) 中包含了五个常数 \(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}\) 和 \(\rho\), 它们是这个分布的参数, 其可 取值的范围为:

\(-\infty<a<\infty,-\infty<b<\infty, \sigma_{1}>0, \sigma_{2}>0,-1<\rho<1\). 常把这个分布记为 \(N\left(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)\). 这函数 (在三维空间中) 的 图形, 好像一个椭圆切面的钟倒扣在 \(O x_{1} x_{2}\) 平面上, 其中心在 \((a, b)\) 点.

为了证明 (2.7) 式确实是一个密度函数, 还须证明 (2.6) 式成 立. 为此, 作变数代换

\[ u=\left(1-\rho^{2}\right)^{-1 / 2} \frac{x_{1}-a}{\sigma_{1}}, v=\left(1-\rho^{2}\right)^{-1 / 2} \frac{x_{2}-b}{\sigma_{2}} \]

得

\[ \begin{aligned} & \iint_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \\ & \quad=\frac{1}{2 \pi} \sqrt{1-\rho^{2}} \iint_{-\infty}^{\infty} \exp \cdot\left[-\frac{1}{2}\left(u^{2}-2 \rho u v+v^{2}\right)\right] \mathrm{d} u \mathrm{~d} v \end{aligned} \]

再作变数代换 \(t_{1}=u-\rho v, t_{2}=\sqrt{1-\rho^{2}} v\). 注意到 \(u^{2}-2 \rho u v+v^{2}=\) \((u-\rho u)^{2}+\left(1-\rho^{2}\right) v^{2}=t_{1}^{2}+t_{2}^{2}\), 且变换的贾可比行列式为

\[ \left|\begin{array}{ll} \partial t_{1} / \partial u & \partial t_{1} / \partial v \\ \partial t_{2} / \partial u & \partial t_{2} / \partial v \end{array}\right|=\left|\begin{array}{cc} 1 & -\rho \\ 0 & \sqrt{1-\rho^{2}} \end{array}\right|=\sqrt{1-\rho^{2}} \]

得

\[ \iint_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \]

\[ \begin{aligned} & =\frac{1}{2 \pi} \sqrt{1-\rho^{2}}\left(\sqrt{1-\rho^{2}}\right)^{-1} \iint_{-\infty}^{\infty} \exp \cdot\left[-\frac{1}{2}\left(t_{1}^{2}+t_{2}^{2}\right)\right] \mathrm{d} t_{1} \mathrm{~d} t_{2} \\ & =(2 \pi)^{-1} \int_{0}^{\infty} \mathrm{e}^{-t_{1}^{2} / 2} \mathrm{~d} t_{1} \int_{0}^{\infty} \mathrm{e}^{-t_{2}^{2} / 2} \mathrm{~d} t_{2} \\ & =(2 \pi)^{-1} \sqrt{2 \pi} \sqrt{2 \pi}=1 \end{aligned} \]

这里用到(1.15).

类似地可定义 \(n\) 维正态分布的概率密度函数, 这里不细讲 了.

在结束这一段之前, 让我们指出几点有关事项：

1. 不论在一维或多维, 在定义连续型随机变量时, 实质之点 都在于它有概率密度函数存在, 即存在有函数 \(f\), 满足 (1.13) 或 (2.5)式. 在概率论理论上, 把这一点直接取为连续型随机变量的 定义: 它就是有密度函数的随机变量. 至于它可以在一个区间或区 域上连续取值倒不是本质的, 甚至也是不确切的.
2. 与离散型随机向量的定义不 同,连续型随机向量不能简单地定义为 “其各分量都是一维连续型随机变量的 那种随机向量”。举一个例子: 设 \(X_{1}\) ～ \(R(0,1), X_{2}=X_{1}\), 则随机 向量 \(\left(X_{1}, X_{2}\right)\) 的两个分量 \(X_{1}, X_{2}\) 都是连续 型的. 但 \(\left(X_{1}, X_{2}\right)\) 却只能在图 2.8 中所 示的单位正方形的对角线 (图中的虚

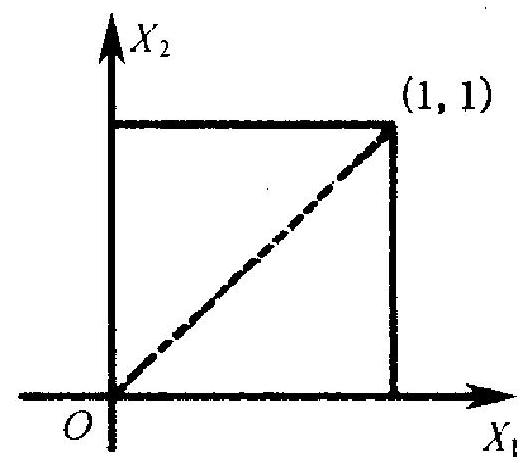
图 2.8 线)上取值. 因而不可能存在一个函数 \(f\left(x_{1}, x_{2}\right)\) 满足 (2.6) 式 (二元函数在平面上任一线段上的积分都 是 0\()\), 即 \(\left(X_{1}, X_{2}\right)\) 的概率密度函数不存在.

1. 与一维情况一样, 也可以用概率分布函数去描述多维随机 向量的概率分布, 其定义为

\[ F\left(x_{1}, x_{2}, \cdots, x_{n}\right)=P\left(X_{1} \leqslant x_{1}, X_{2} \leqslant x_{2}, \cdots, X_{n} \leqslant x_{n}\right) \]

然耐, 在多维情况下, 分布函数极少应用.

2. 2 .3 边练分布

设 \(X=\left(X_{1}, \cdots, X_{n}\right)\) 为一 \(n\) 维随机向量. \(X\) 有一定的分布 \(F\), 这是一个 \(n\) 维分布. 因为 \(X\) 的每个分量 \(X_{i}\) 都是一维随机变量, 故 它们都有各自的分布 \(F_{i}, i=1, \cdots, n\), 这些都是一维分布, 称为随 机向量 \(X\) 或其分布 \(F\) 的“边缘分布”. 以下我们要指出: 边缘分布 完全由原分布 \(F\) 确定,且从这个事实的讲解中也就悟出“边缘”一 词的含义.

表 2.1

\(x_{1}>x\)	-1	0	5	行合计
1	0.17	0.05	0.21	0.43
3	0.04	0.28	0.25	0.57
列合计	0.21	0.33	0.46	1.00

例 2.6 表 2.1 以列表的形式, 显示了一个二维随机向量 \(X\) \(=\left(X_{1}, X_{2}\right)\) 的概率分布. 比如

\[ P\left(X_{1}=1, X_{2}=5\right)=0.21 \]

等等. 现在如想求 \(X_{1}\) 的分布, 则先注意到, \(X_{1}\) 只有两个可能值, 即 1 和 3. 而 \(\left\{X_{1}=1\right\}\) 这个事件可以分解为三个互斥事件

\[ \left\{X_{1}=1, X_{2}=-1\right\},\left\{X_{1}=1, X_{2}=0\right\},\left\{X_{1}=1, X_{2}=5\right\} \]

之和, 故其概率应为上述三事件概率之和, 即

\[ P\left(X_{1}=1\right)=0.17+0.05+0.21=0.43 \]

类似地得 \(P\left(X_{1}=3\right)=0.04+0.28+0.25=0.57\). 用同样的方法 确定 \(X_{2}\) 的概率分布为

\[ P\left(X_{2}=-1\right)=0.21, P\left(X_{2}=0\right)=0.33, P\left(X_{2}=5\right)=0.46 \]

注意这两个分布正好是表的中央部分的行和与列和. 它们都处在 表的“边缘”位置上. 由此得出边缘分布这个名词. 也有称为边际分 布的. 从这个例子就不难悟出, 在一般的离散型情况下, 怎样去求边 缘分布. 回到定义 2.1 的记号, 以 \(X_{1}\) 为例, 它的全部可能值为 \(a_{11}, a_{12}, a_{13}, \cdots\). 例如, 我们要求 \(P\left(X_{1}=a_{1 k}\right)\). 它等于把 \((2.1)\) 式 那样的概率全加起来,但局限于 \(j_{1}=k\) (这相当于在上述简例 2.6 中求行和或列和). 得

\[ P\left(X_{1}=a_{1 k}\right)=\sum_{j_{2}, \cdots, j_{n}} p\left(k, j_{2}, \cdots, j_{n}\right), k=1,2, \cdots \]

例 2.7 设 \(X=\left(X_{1}, \cdots, X_{n}\right)\) 服从多项分布 \(M\left(N ; p_{1}, \cdots\right.\), \(\left.p_{n}\right)\), 要求其边缘分布. 例如, 考虑 \(X_{1}\), 我们把事件 \(A_{1}\) 作为一方, \(A_{2}+\cdots+A_{n}\) 作为一方 (它就是 \(\bar{A}_{1}\) ), 见例 2.2 的说明, 那么, \(X_{1}\) 就 是在 \(N\) 次独立试验中,事件 \(A_{1}\) 发生的次数,而在每次试验中 \(A_{1}\) 发生的概率保持为 \(p_{1}\), 经过这一分析, 不待计算就可以明了: \(X_{1}\) 的分布就是二项分布 \(B\left(N, p_{1}\right)\). 应用公式 (2.8) 也可以得出这个 结果:按 (2.8), 注意到多项分布的形式 (2.3), 有

\[ P\left(X_{1}=k\right)=\sum_{k_{2}, \cdots, k_{n}}^{\prime} \frac{N !}{k_{2} ! \cdots k_{n} !} p_{2}^{k_{2} \cdots} p_{n^{n}}^{k_{n}} \cdot p_{1}^{k} / k ! \]

这里, \(\sum_{k_{2}, \cdots, k_{n}}^{\prime}\) 表示求和的范围为: \(k_{2}, \cdots, k_{n}\) 都是非负整数, 其和为 \(N-k\). 令

\[ p_{2}^{\prime}=p_{2} /\left(1-p_{1}\right), \cdots, p_{n}^{\prime}=p_{n} /\left(1-p_{1}\right) \]

则 \(p_{2}^{\prime}+\cdots+p_{n}^{\prime}=\left(p_{2}+\cdots+p_{n}\right) /\left(1-p_{1}\right)=\left(1-p_{1}\right) /\left(1-p_{1}\right)=\) 1 , 且可把上式改写为

\[ \begin{aligned} P\left(X_{1}=k\right)= & \sum_{k_{2}, \cdots, k_{n}}^{\prime} \frac{(N-k) !}{k_{2} ! \cdots k_{n} !} p_{2}^{\prime k_{2} \cdots p_{n}^{\prime k_{n}}} \\ & \cdot \frac{N !}{k !(N-k) !} p_{1}^{k}\left(1-p_{1}\right)^{N-k} \end{aligned} \]

按多项展开式 (2.4), 上式右边第一因子为

\[ \left(p_{2}^{\prime}+\cdots+p_{n}^{\prime}\right)^{N-k}=1^{N-k}=1 \]

于是得到

\[ P\left(X_{1}=k\right)=\frac{N !}{k !(N-k) !} p_{1}^{k}\left(1-p_{1}\right)^{N-k} \]

\[ =b\left(k ; N, p_{1}\right), k=0,1, \cdots, N \]

正是二项分布 \(B\left(N, p_{1}\right)\).

现在来考虑连续型随机向量的边缘分布. 为书写简单计, 先考 虑二维的情况, 设 \(X=\left(X_{1}, X_{2}\right)\) 有概率密度函数 \(f\left(x_{1}, x_{2}\right)\). 我们 来证明: 这时 \(X_{1}\) 和 \(X_{2}\) 都具有概率密度函数.

为证明这一点, 考虑 \(X_{1}\) 的分布函数 \(F_{1}\left(x_{1}\right)=P\left(X_{1} \leqslant x_{1}\right)\). 它可以写为 \(P\left(X_{1} \leqslant x_{1}, X_{2}<\infty\right)\). 注意到公式 \((2.5)\), 得

\[ F_{1}\left(x_{1}\right)=P\left(X_{1} \leqslant x_{1}\right)=\int_{-\infty}^{x_{1}} \mathrm{~d} t_{1} \int_{-\infty}^{\infty} f\left(t_{1}, t_{2}\right) \mathrm{d} t_{2} \]

\(\int_{-\infty}^{\infty} f\left(t_{1}, t_{2}\right) \mathrm{d} t_{2}\) 是 \(t_{1}\) 的函数, 记之为 \(f_{1}\left(t_{1}\right)\). 于是上式可写为

\[ F_{1}\left(x_{1}\right)=\int_{-\infty}^{x_{1}} f_{1}\left(t_{1}\right) \mathrm{d} t_{1} \]

两边对 \(x_{1}\) 求导数, 得到 \(X_{1}\) 的概率密度函数为

\[ \mathrm{d} F_{1}\left(x_{1}\right) / \mathrm{d} x_{1}=f_{1}\left(x_{1}\right)=\int_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{2} \]

这不仅证明了 \(X_{1}\) 的密度函数的存在, 而且还推出了其公式. 同理 求出 \(X_{2}\) 的密度函数为

\[ f_{2}\left(x_{2}\right)=\int_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \]

这个结果很容易推广到 \(n\) 维的情形: 设 \(X=\left(X_{1}, \cdots, X_{n}\right)\) 有概率 密度函数 \(f\left(x_{1}, \cdots, x_{n}\right)\). 为求某分量 \(X_{i}\) 的溉率密度函数, 只须把 \(f\left(x_{1}, \cdots, x_{n}\right)\) 中的 \(x_{i}\) 固定, 然后对 \(x_{1}, \cdots, x_{i-1}, x_{i+1}, \cdots, x_{n}\) 在 \(\infty\) 到 \(\infty\) 之间作定积分. 例如, \(X_{1}\) 的密度函数为

\[ f_{1}\left(x_{1}\right)=\int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} f\left(x_{1}, x_{2}, \cdots, x_{n}\right) \mathrm{d} x_{2} \cdots \mathrm{d} x_{n} \]

例 2.8 再考虑例 2.3. 用公式 (2.9), (2.10) 很容易确定, \(X_{1}, X_{2}\) 的边缘分布分别是均匀分布 \(R(a, b)\) 和 \(R(c, d)\). 计算很 容易,留给读者.

例 2.9 考虑例 2.4. 按 (2.9), \(X_{1}\) 的边缘密度函数为

\[ f_{1}\left(x_{1}\right)=\pi^{-1} \int_{-\infty}^{\infty}\left(1+x_{1}^{2}+x_{2}^{2}\right)^{-2} \mathrm{~d} x_{2} \]

作变数代换 \(t=x_{2} / \sqrt{1+x_{1}^{2}}\), 得

\[ f_{1}\left(x_{1}\right)=\pi^{-1}\left(1+x_{1}^{2}\right)^{-3 / 2} \int_{-\infty}^{\infty}\left(1+t^{2}\right)^{-2} \mathrm{~d} t=\frac{1}{2}\left(1+x_{1}^{2}\right)^{-3 / 2} \]

积分 \(\int_{-\infty}^{\infty}\left(1+t^{2}\right)^{-2} \mathrm{~d} t\) 通过变数代换 \(t=\tan \theta\) 很易算出.

例 2.10 二维正态分布 \(N\left(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)\) 的边缘分布密度. 若 \(\left(X_{1}, X_{2}\right)\) 有二维正态分布 \(N\left(a, b, \sigma_{2}^{1}, \sigma_{2}^{2}, \rho\right)\), 我们来证明: \(X_{1}\), \(X_{2}\) 的边缘分布分别是一维正态分布 \(N\left(a, \sigma_{1}^{2}\right)\) 和 \(N\left(b, \sigma_{2}^{2}\right)\). 为证 此,要计算 \(\int_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{2}\), 其中 \(f\) 由 (2.7)式定义. 迬意到

\[ \begin{gathered} \frac{\left(x_{1}-a\right)^{2}}{\sigma_{1}^{2}}-\frac{2 \rho\left(x_{1}-a\right)\left(x_{2}-b\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(x_{2}-b\right)^{2}}{\sigma_{2}^{2}} \\ =\left(1-p^{2}\right) \frac{\left(x_{1}-a\right)^{2}}{\sigma_{1}^{2}}+\left(\rho \frac{x_{1}-a}{\sigma_{1}}-\frac{x_{2}-b}{\sigma_{2}}\right)^{2} \end{gathered} \]

得到

\[ \begin{aligned} f_{1}\left(x_{1}\right)= & \int_{-\infty}^{\infty} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{2}=\left(2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}\right)^{-1} \\ & \cdot \exp \left(-\frac{\left(x_{1}-a\right)^{2}}{2 \sigma_{1}^{2}}\right) C \end{aligned} \]

其中

\[ C=\int_{-\infty}^{\infty} \exp \left[-\frac{1}{2\left(1-\rho^{2}\right)}\left(\rho \frac{x_{1}-a}{\sigma_{1}}-\frac{x_{2}-b}{\sigma_{2}}\right)^{2}\right] \mathrm{d} x_{2} \]

作变数代换 (注意 \(x_{1}\) 为常数,非积分变量)

\[ t=\left(\frac{x_{2}-b}{\sigma_{2}}-\rho \frac{x_{1}-a}{\sigma_{1}}\right) / \sqrt{1-\rho^{2}} \]

得

\[ C=\int_{-\infty}^{\infty} \exp \left(-t^{2} / 2\right) \mathrm{d} t \cdot \sigma_{2} \sqrt{1-\rho^{2}}=\sqrt{2 \pi} \sigma_{2} \sqrt{1-\rho^{2}} \]

以此代入前式, 即得

\[ f_{1}\left(x_{1}\right)=\left(\sqrt{2 \pi} \sigma_{1}\right)^{-1} \exp \left(-\frac{\left(x_{1}-a\right)^{2}}{2 \sigma_{1}^{2}}\right) \]

这正是 \(N\left(a, \sigma_{1}^{2}\right)\) 的概率密度函数.

从这个例子看出一个有趣的事实: 虽则一个随机向量 \(X=\) \(\left(X_{1}, \cdots, X_{n}\right)\) 的分布 \(F\) 足以决定其任一分量 \(X_{i}\) 的 (边缘) 分布 \(F_{i}\), 但反过来不对: 即使知道了所有 \(X_{i}\) 的边缘分布 \(F_{i}, i=1, \cdots, n\), 也 不足以决定 \(X\) 的分布 \(F\). 例如,考虑两个二维正态分布

\[ N(0,0,1,1,1 / 3) \text { 和 } N(0,0,1,1,2 / 3) \]

它们的任一边缘分布都是标准正态分布 \(N(0,1)\), 但这两个二维 分布是不同的分布, 因为 \(\rho\) 的数值不相同. 这个现象的解释是: 边 缘分布只分别考虑了单个变量 \(X_{i}\) 的情况, 而末涉及它们之间的 关系, 而这个信息却是包含在 \(\left(X_{1}, \cdots, X_{n}\right)\) 的分布之内的. 如就本 例来说, 在下一章 (见第三章 3.3 节) 将指出: \(\rho\) 这个参数正好刻画 了两分量 \(X_{1}\) 和 \(X_{2}\) 之间的关系.

在结束这一节之前, 我们再强调指出: “边缘”分布就是通常的 分布, 并无任何特殊的含义. 如果说有什么意思的话, 它不过是强 调了: 这个分布是由于 \(X_{i}\) 作为随机向量 \(\left(X_{1}, \cdots, X_{n}\right)\) 之一分量, 从后者的分布中派生出的分布而已, 别无其他. 至于 “边缘”一泀的 由来,已在例 2.6 中解释过了.

与此相应, 为了强调 \(\left(X_{1}, \cdots, X_{n}\right)\) 的分布是把 \(X_{1}, \cdots, X_{n}\) 作为 一个有联系的整体来考虑, 有时把它称为 \(X_{1}, \cdots, X_{n}\) 的 “联合分 布”。

另外, 边缘分布也可以不只是单个的. 例如 \(X=\left(X_{1}, X_{2}, X_{3}\right)\) 它的分布也决定了其任一部分, 例如 \(\left(X_{1}, X_{3}\right)\) 的二维分布, 这也称 为边缘分布. 有关公式也不难导出, 此处不细讲了.

评论

登录github的账号后，可以直接在下方评论框中输入。

如果想进行更详细的讨论(如排版、上传图片等)，选择一个反应后并点击上方的文字，进入论坛页面。