6.4 相关分析⚓︎

在相关分析中, 所涉及的变量都是随机的, 且处于平等的地位,故用 $X_{1}, \cdots, X_{p}$ 来记, 而不用 $Y$.

\title{ 6.4.1 相关系数的估计和检验 }

设 $\left(X_{1}, X_{2}\right)$ 服从二维正态分布 $N\left(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)$, 其概率密度函数见第二章 (2.7) 式. 在第三章指出: $a, \sigma_{1}^{2}$ 分别是 $X_{1}$ 的均值方差, $b, \sigma_{2}^{2}$ 分别是 $X_{2}$ 的均值方差, 而 $\rho$ 是 $X_{1}, X_{2}$ 之间的相关系数. 在 3.3 节中仔细论述了相关系数的意义, 尤其是指出了: 当总体分布为正态时, 相关系数确实是变量之间的相关性的合理指标,

324 • 而在非正态情况则只是线性相关程度的度量.

相关系数 $\rho$ 的公式是

\[ \rho=\operatorname{Cov}\left(X_{1}, X_{2}\right) /\left(\operatorname{Var}\left(X_{1}\right) \operatorname{Var}\left(X_{2}\right)\right)^{1 / 2} \]

这个公式启发了 $\rho$ 的一个估计方法, 即矩估计法. 设 $\left(X_{11}, X_{21}\right)$, $\cdots,\left(X_{1 n}, X_{2 n}\right)$ 为 $\left(X_{1}, X_{2}\right)$ 的 $n$ 个独立同分布的观察值, 按矩法, 分别以 $\left(\bar{X}_{j}=\sum_{i=1}^{n} X_{j i} / n, j=1,2\right)$

\[ \begin{aligned} & \sum_{i-1}^{n}\left(X_{1 i}-\bar{X}_{1}\right)^{2} /(n-1), \sum_{i=1}^{n}\left(X_{2 i}-\bar{X}_{2}\right)^{2} /(n-1) \text { 和 } \\ & \sum_{i=1}^{n}\left(X_{1 i}-\bar{X}_{1}\right)\left(X_{2 i}-\bar{X}_{2}\right) /(n-1) \end{aligned} \]

去估计 $\operatorname{Var}\left(X_{1}\right), \operatorname{Var}\left(X_{2}\right)$ 和 $\operatorname{Cov}\left(X_{1}, X_{2}\right)$. 由此, 按 (4.1), 得出 $\rho$ 的估计为

\[ r=\frac{\sum_{i=1}^{n}\left(X_{1 i}-\bar{X}_{1}\right)\left(X_{2 i}-\bar{X}_{2}\right)}{\left[\sum_{i=1}^{n}\left(X_{1 i}-\bar{X}_{1}\right)^{2} \sum_{i=1}^{n}\left(X_{2 i}-\bar{X}_{2}\right)^{2}\right]^{1 / 2}} \]

$r$ 称为 “样本相关系数”.

对 $\rho$ 的检验, 最有兴趣的是原假设

\[ H_{0}: \rho=0 \]

对立假设为 $\rho \neq 0 . H_{0}$ 表示 $X_{1}, X_{2}$ 独立 (在第三章已指出这在非正态情况下不成立). 一个显然的检验方法是: 计算 $r$,

\[ \text { 当 }|r| \leqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

常数 $C$ 与样本大小 $n$ 及检验水平 $\alpha$ 有关. 要决定 $C$, 必须求出在 $\rho=0$ 时样本相关系数 $r$ 的分布. 这分布不很复杂, 但我们这里无法介绍推导过程了, 只指出: 当 $\rho=0$ 时有 ${ }^{*}$

\[ \sqrt{n-2} r / \sqrt{1-r^{2}} \sim t_{n-2} \]

由于 $|r| \leqslant C$ 等价于 $\left|\sqrt{n-2} r / \sqrt{1-r^{2}}\right| \leqslant \sqrt{n-2} C / \sqrt{1-C^{2}}$,

证明见习题 8 . 由 (4.5) 不难定出: 当给定检验水平 $\alpha$ 时, (4.4) 中的 $C$ 应取为方程 $\sqrt{n-2} C / \sqrt{1-C^{2}}=t_{n-2}(\alpha / 2)$ 之解, 即

\[ C=t_{n-2}(\alpha / 2) / \sqrt{n-2+t_{n-2}^{2}(\alpha / 2)} \]

对 $n=20,30, \cdots, 100$, 由 (4.6) 算出的 $C$, 为 $(\alpha=0.05)$

\[\begin{tabular}{c|ccccccccc} \hline$n$ & 20 & 30 & 40 & 50 & 60 & 70 & 80 & 90 & 100 \\ \hline$C$ & $0 .+41$ & 0.360 & 0.328 & 0.290 & $0.25+$ & 0.235 & 0.220 & 0.207 & 0.197 \\ \hline \end{tabular}\]

当样本大小 $n$ 为 20 时, 即使样本相关系数 $r$ 达到 \pm 0.4 , 尚不足以推断 $\rho$ 异于 0 . 随着 $n$ 增加, 这个界限逐步下降, 但即使 $n$ 达到 100 , 这个界限也还大约在 0.2 . 这说明: 要发现两变量之间较微弱的相关, 样本大小 $n$ 必须很大才行. 同时也说明了: 对较小的 $n, r$ 的精度很差, 意义不大。

当 $\rho \neq 0$ 时样本相关系数 $r$ 的分布问题, 在本世纪初曾是 $\mathrm{K}$. 皮尔逊和 R. A. 费歇尔等统计学大师着力研究的对象, 最后被费歇尔在 1915 年解决了, 其形式极为复杂, 在此不能细述了.

\section{4 .2 偏相关}

在统计学上, 相关系数作为随机变量之间相关程度的刻画, 用得很多, 但在其解释上则应注意几点: 一是统计相关不能等同于因果关系, 这一点我们在第三章中已指出过了. 例如, 分别以 $X_{1}, X_{2}$ 记一个人的饮食和衣着消费, 则 $X_{1}, X_{2}$ 有较强的相关. 但很难说这: 者有何因果关系: 说好吃的人多半好穿, 或者好穿的人多半好吃, 末见得可信. 但既然如此, 为什么在观察结果上又会显示出较强的相关呢? 这就涉及到另一个.需要注意之点: 所考虑的变量 (如此处的 $X_{1}, X_{2}$ ) 并非孤立的, 它们除彼此可能有的影响外, 还受到 - - 大批其他变理 (不妨暂称为 $X_{3}, \cdots, X_{p}$ 等) 的影响. 由于这个原因, 相关系数有时被称为 “完全相关系数”. 意思是说, 在其中总结了由一切影响带来的相关性. 这个说法解释了上百提出的那个问题: 为何看来彼此并无密切因果关系的变量, 在观察结果上会显示出较强的相关. 这原因就在于被其他因素带动起来了. 拿上例来说, 如以 $X_{3}$ 记人的收人, 则一般说来, 收人大的人各方面消费都倾向于高, 它带动了 $X_{1}$ (吃)和 $X_{2}$ (穿)增长, 以致使二者显示出较强的正相关. 可以设想, 如果能用某种方式把 $X_{3}$ 的影响消去, 则 $X_{1}, X_{2}$ 可能显示很不一样的相关性质. 例如它可以转为负相关. 因为在一定收人的人中, 在吃、穿中的一个方面消费大的人, 一般会导致另一方面消费的减少.

一般, 设有 $p$ 个随机变量 $X_{1}, X_{2}, X_{3}, \cdots, X_{p}$. 把 $X_{3}, X_{4}, \cdots$, $X_{p}$ 的影响从 $X_{1}, X_{2}$ 中消去, 剩余的部分分别记为 $X_{1}{ }^{\prime}$ 和 $X_{2}{ }^{\prime}$. 则 $X_{1}^{\prime}, X_{2}{ }^{\prime}$ 的相关系数称为 $X_{1}, X_{2}$ 对 $\left(X_{3} \cdots, X_{p}\right)$ 的偏相关系数, 并记为 $\rho_{12} \cdot(3+\cdots p)$. 在以上论述中, “消去”一词的含义并末严格界定, 但一般是在最小二乘法的意义下.例如, 从 $X_{1}$ 中消去 $X_{3}, \cdots, X_{p}$ 的影响, 指的是找一个线性式

\[ L_{1}\left(X_{3}, \cdots, X_{p}\right)=c_{0}+c_{3} X_{3}+\cdots+c_{p} X_{p} \]

使 $E\left[X_{1}-L_{1}\left(X_{3}, \cdots, X_{p}\right)\right]^{2}$ 达到最小,剩余就是

\[ X_{1}^{\prime}=X_{1}-L_{1}\left(X_{3}, \cdots, X_{p}\right) \]

同理找线性式 $L_{2}\left(X_{3}, \cdots, X_{p}\right)=d_{0}+d_{3} X_{3}+\cdots+d_{p} X_{p}$, 使 $\mathrm{E}\left[X_{2}-\right.$ $\left.L_{2}\left(X_{3}, \cdots, X_{p}\right)\right]^{2}$ 最小,剩余是

\[ X_{2}^{\prime}=X_{2}-L_{2}\left(X_{3}, \cdots, X_{p}\right) \]

$X_{1}, X_{2}$ 对 $\left(X_{3}, \cdots, X_{p}\right)$ 的偏相关系数 $\rho_{12} \cdot(3+\cdots p)$ 就是 $X_{1}^{\prime}, X_{2}^{\prime}$ 的相关系数. 要算出其表达式, 就需要算出上文的线性式 $L_{1}$ 和 $L_{2}$. 下面我们对 $p=3$ 这个简单情况来计算一下. 分别以 $a_{1}, a_{2}, a_{3} ; \sigma_{1}^{2}$, $\sigma_{2}^{2}, \sigma_{3}^{2}$ 记 $X_{1}, X_{2}$ 和 $X_{3}$ 的均值和方差, 以 $\rho_{12}, \rho_{13}, \rho_{23}$ 分别记 $X_{1}$, $X_{2}$ 之间, $X_{1}, X_{3}$ 之间, 和 $X_{2}, X_{3}$ 之间的相关系数.

关于找一个线性式 $L_{1}\left(X_{3}\right)$ 使 $E\left(X_{1}-L_{1}\left(X_{3}\right)\right)^{2}$ 达到最小的问题, 已在 3.3 节中讨论过了, 按该章的 (3.5) 式, 用此处的记号, 有

\[ L_{1}\left(X_{3}\right)=a_{1}+\sigma_{1} \sigma_{3}^{-1} \rho_{13}\left(X_{3}-a_{3}\right) \]

同理有

\[ L_{2}\left(X_{3}\right)=a_{2}+\sigma_{2} \sigma_{3}^{-1} \rho_{23}\left(X_{3}-a_{3}\right) \]

故有

\[ \begin{aligned} & X_{1}^{\prime}=X_{1}-a_{1}-\sigma_{1} \sigma_{3}^{-1} \rho_{13}\left(X_{3}-a_{3}\right) \\ & X_{2}^{\prime}=X_{2}-a_{2}-\sigma_{2} \sigma_{3}^{-1} \rho_{23}\left(X_{3}-a_{3}\right) \end{aligned} \]

显然, $E\left(X_{1}^{\prime}\right)=E\left(X_{2}^{\prime}\right)=0$, 而按第三章 (3.6) 式, 用此处的记号, 有

\[ \operatorname{Var}\left(X_{1}^{\prime}\right)=\sigma_{1}^{2}\left(1-\rho_{13}^{2}\right), \operatorname{Var}\left(X_{2}^{\prime}\right)=\sigma_{2}^{2}\left(1-\rho_{23}^{2}\right) \]

而

\[ \begin{aligned} \operatorname{Cov} & \left(X_{1}^{\prime}, X_{2}^{\prime}\right)=E\left(X_{1}^{\prime}, X_{2}^{\prime}\right)=E\left[\left(X_{1}-a_{1}\right)\left(X_{2}-a_{2}\right)\right] \\ & -\sigma_{1} \sigma_{3}^{-1} \rho_{13} E\left[\left(X_{3}-a_{3}\right)\left(X_{2}-a_{2}\right)\right] \\ & -\sigma_{2} \sigma_{3}^{-1} \rho_{23} E\left[\left(X_{1}-a_{1}\right)\left(X_{3}-a_{3}\right)\right] \\ & +\sigma_{1} \sigma_{3}^{-1} \rho_{13} \sigma_{2} \sigma_{3}^{-1} \rho_{23} E\left[\left(X_{3}-a_{3}\right)\right]^{2} \\ = & \sigma_{1} \sigma_{2} \rho_{12}-\sigma_{1} \sigma_{3}^{-1} \rho_{13} \sigma_{2} \sigma_{3} \rho_{23} \\ & -\sigma_{2} \sigma_{3}^{-1} \rho_{23} \sigma_{1} \sigma_{3} \rho_{13}+\sigma_{1} \sigma_{2} \sigma_{3}^{-2} \rho_{13} \rho_{23} \sigma_{3}^{2} \\ = & \sigma_{1} \sigma_{2} \rho_{12}-\sigma_{1} \sigma_{2} \rho_{13} \rho_{23}=\sigma_{1} \sigma_{2}\left(\rho_{12}-\rho_{13} \rho_{23}\right) \end{aligned} \]

由 $(4.7),(4.8)$, 得

\[ \begin{aligned} \rho_{12 \cdot(3)} & =\operatorname{Corr}\left(X_{1}^{\prime}, X_{2}^{\prime}\right) \\ & =\operatorname{Cov}\left(X_{1}^{\prime}, X_{2}^{\prime}\right) /\left(\operatorname{Var}\left(X_{1}^{\prime}\right) \operatorname{Var}\left(X_{2}^{\prime}\right)\right)^{1 / 2} \\ & =\left(\rho_{12}-\rho_{13} \rho_{23}\right) /\left[\left(1-\rho_{13}^{2}\right)\left(1-\rho_{23}^{2}\right)\right]^{1 / 2} \end{aligned} \]

细察表达式 (4.9), 有如下的构造: 把 $X_{1}, X_{2}, X_{3}$ 之间的相关系数, 连同 $X_{i}$ 与 $X_{i}$ 之间的相关系数 $\rho_{i i}=1$ 也在内, 排列成一个三阶方阵 (称为 $X_{1}, X_{2}, X_{3}$ 的 “相关阵”)

\[ P=\left(\begin{array}{lll} \rho_{11} & \rho_{12} & \rho_{13} \\ \rho_{21} & \rho_{22} & \rho_{23} \\ \rho_{31} & \rho_{32} & \rho_{33} \end{array}\right)=\left(\begin{array}{ccc} 1 & \rho_{12} & \rho_{13} \\ \rho_{12} & 1 & \rho_{23} \\ \rho_{13} & \rho_{23} & 1 \end{array}\right) \]

此处用了 $\rho_{i i}=1, \rho_{i j}=\rho_{j i}$. 则其 $(1,1)$ 元的子式, 即划掉 $P$ 的第一行第一列所剩下的行列式, 等于 $P_{11}=1-\rho_{2}^{2}$. 同样, $(2,2)$ 元的子式为 $P_{22}=1-\rho_{13}^{2},(1,2)$ 元的子式为 $P_{12}=\rho_{12}-\rho_{13} \rho_{23}$. 因此

\[ \rho_{12 \cdot(3)}=P_{12} / \sqrt{P_{11} P_{22}} \]

这个表达式,可以证明,能推广到 $p$ 个自变量 $X_{1}, X_{2}, X_{3}, X_{p}$ 的情况. 仍以 $\rho_{i j}$ 记 $X_{i}, X_{j}$ 之间的相关系数 $\left(\rho_{i i}=1, \rho_{i j}=\rho_{j i}\right), P$ 记其相关阵:

\[ P=\left(\begin{array}{cccc} \rho_{11} & \rho_{12} & \cdots & \rho_{1 p} \\ \rho_{21} & \rho_{22} & \cdots & \rho_{2 p} \\ \vdots & \vdots & & \vdots \\ \rho_{p 1} & \rho_{p 2} & \cdots & \rho_{p p} \end{array}\right) \]

而以 $P_{u v}$ 记 $P$ 的 $(u, v)$ 元的子式, 即从 $P$ 中划去第 $u$ 行第 $v$ 列所成的行列式,则

\[ \rho_{12 \cdot(34 \cdots p)}=P_{12} / \sqrt{P_{11} P_{22}} \]

从表达式 (4.9) 看出一个现象. 设 $\rho_{12}>0$, 但不太接近于 1. 即 $X_{1}$, $X_{2}$ 为正相关, 但相关程度不是非常密切. 又 $\rho_{13}, \rho_{23}$ 都很接近 1 , 则 (4.9)式之分子将小于 0 , 即 $\rho_{12 \cdot(3)}<0$. 就是说, 尽管 $X_{1}, X_{2}$ 的通常相关系数为正, 其偏相关系数可以为负. 这拿前面举的那个 $X_{1}$ $=$ 吃的支出, $X_{2}=$ 穿的支出, $X_{3}=$ 收人的例子可作一个印证. $X_{1}$, $X_{2}$ 的 (完全) 相关 $\rho_{12}$ 大于 0 , 但 $\rho_{13}, \rho_{23}$ 看来都为正且很大, 故 $\rho_{12} \cdot(3)$ 当小于 0 : 从吃穿支出中消去收人的影响, 等于在固定收人的情况下考虑二者的关系, 其相关为负就不难理解了. 当然, 反过来也可能:即 $\rho_{12}<0$ 但 $\rho_{12} \cdot(3)>0$.

因此,在涉及多个变量相互影响的问题中,不仅考虑完全相关系数, 而且考虑种种有意义的偏相关系数(在全部 $p$ 个自变量中, 可任选出 $k \geqslant 3$ 个: $X_{i_{1}}, \cdots, X_{i_{k}}$, 而考虑 $X_{i_{1}}, X_{i_{2}}$ 对 $\left(X_{i_{3}}, \cdots, X_{i_{k}}\right)$ 的偏相关系数. 其计算仍按 (4.11), 只是在 $P$ 中要把不是 $i_{1}, \cdots, i_{k}$ 那些行列都划去), 这样对整个相关的图景就可获得深人一层的了解.

读者也不要误以为偏相关系数高于完全相关系数, 这二者各说明“相关”这个概念的一个侧面, 其含义不同. 在什么情况下哪一种相关更为贴切,要看问题的性质.

如果对 $\left(X_{1}, \cdots, X_{p}\right)$ 进行了 $n$ 次观察, 得样本

\[ \left(X_{1 i}, \cdots, X_{p i}\right), i=1, \cdots, n \]

则可以用前面的方法 (见(4.2) 式) 估计 $X_{u}$ 与 $X_{v}$ 的相关系数, 即计算样本相关系数 $r_{u(i-1}$ :

\[ \begin{aligned} r_{u i}= & \sum_{i=1}^{n}\left(X_{u i}-\bar{X}_{u}\right)\left(X_{v i}-\bar{X}_{u}\right) /\left[\sum_{i=1}^{n}\left(X_{u i}-\bar{X}_{u}\right)^{2}\right. \\ & \left.\cdot \sum_{i=1}^{n}\left(X_{i i}-\bar{X}_{v}\right)^{2}\right] 1 / 2 \end{aligned} \]

其中 $\bar{X}_{k}=\left(X_{k 1}+\cdots+X_{k n}\right) / n, k=1, \cdots, p$. 有 $r_{u t u}=1, r_{u u^{\prime}}=r_{v u}$. 以 $r_{u v}$, 代替 $P$ 中的 $\rho_{u v}$ 得样本相关阵

\[ R=\left[\begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1 p} \\ r_{21} & r_{22} & \cdots & r_{2 p} \\ \vdots & \vdots & & \vdots \\ r_{p 1} & r_{p 2} & \cdots & r_{p p} \end{array}\right) \]

然后用

\[ r_{12 \cdot(34 \cdots p)}=R_{12} / \sqrt{R_{11} R_{22}} \]

去估计 $r_{12} \cdot(34 \cdots p)$. 它称为样本偏相关系数.

如果要检验有关 $\rho_{12} \cdot(34 \cdots p)$ 的假设, 则必须假定变量服从正态分布. 在这种假定下, 可以证明:原假设

\[ H_{0}: \rho_{12 \cdot(34 \cdots p)}=0 \]

的一个水平 $\alpha$ 的检验为

\[ \left\{\begin{array}{l} \left|r_{12 \cdot(34 \cdots p)}\right| \leqslant t_{n-p}(\alpha / 2) /\left[n-p+t_{n-p}^{2}(\alpha / 2)\right]^{1 / 2}, \text { 接受 } H_{0} \\ \mid r_{12 \cdot(34 \cdots p)}:>t_{n-p}(\alpha / 2) /\left[n-p+t_{n-p}^{2}(\alpha / 2)\right]^{1 / 2} \text {, 否定 } H_{0} \end{array}\right. \]

此检验与前述相关系数为 0 的检验之差别仅在于, 把(4.6) 式中的 $n-2$ 换为 $n-p$.

例 4.1 随机抽取 1000 人调查其 (每年) 吃的支出 $\left(X_{1}\right)$, 衣着支出 $\left(X_{2}\right)$ 和收人 $\left(X_{3}\right)$, 算出的样本相关系数分别为 $r_{12}=0.57$, $r_{13}=0.82, r_{23}=0.80$. 对 $n=1000, \alpha=0.05, t_{n-2}(\alpha / 2)$ 和 $t_{n-3}$ $(\alpha / 2)$ 都可取为 1.96. 于是易算得 $\left|r_{12}\right|>t_{n-2}(\alpha / 2) /$ $\sqrt{n-2+t_{n-2}^{2}(\alpha / 2)}$, 因而 $X_{1}, X_{2}$ 的(完全) 相关在 $\alpha=0.05$ 的水平上为显著的且为正相关. 按公式 (4.9), 算出

\[ r_{12 \cdot(3)}=\left(r_{12}-r_{13} r_{23}\right) / \sqrt{\left(1-r_{13}^{2}\right)\left(1-\overline{r_{23}^{2}}\right)}=-0.73 \]

它在水平 $\alpha=0.05$ 时为高度的负相关.

\section{4 .3 复相关}

设有若干个随机变量 $X_{1}, \cdots, X_{p}$. 可能有这种情况: $X_{1}$ 对每个 $X_{j}(j \geqslant 2)$ 的相关性不一定很鼠著, 但全体 $X_{2}, \cdots, X_{p}$ 合起来, 则与 $X_{1}$ 有较显著的相关. 例如, 设 $X_{1}$ 为某种水田农作物的产量, $X_{2}, \cdots, X_{p}$ 为该作物生长期那几个月的各月降雨量 (例如 $3 、 4 、 5 、 6$ 月 ), 亩产与指定一月的降雨量肯定有关, 但不一定十分大, 而全体这几个月的降雨情况, 则肯定与亩产有更大的相关. 这种以 $X_{1}$ 为一方, $X_{2}, \cdots, X_{p}$ 全体为一方之间的相关, 称为 $X_{1}$ 与 $\left(X_{2}, \cdots, X_{p}\right)$ 的“复相关”.

这种复相关的定义,与偏相关有其相似之处,就是也要找 $X_{2}$, $\cdots, X_{p}$ 的一个线性式 $L\left(X_{2}, \cdots, X_{p}\right)=c_{0}+c_{2} X_{2}+\cdots+c_{p} X_{p}$, 使 $E\left[X_{1}-L\left(X_{2}, \cdots, X_{p}\right)\right]^{2}$ 达到最小. 然后, $X_{1}$ 与 $L\left(X_{2}, \cdots, X_{p}\right)$ 的通常相关系数, 就定义为 $X_{1}$ 和 $\left(X_{2}, \cdots, X_{p}\right)$ 之间的 “复相关系数”, 并记为 $\rho_{1(23 \cdots p)}$.

求 $L\left(X_{2}, \cdots, X_{p}\right)$ 的方法, 与 3.3 节所用方法相似 (那里解决了 $p=2$ 的情况). 仔细推导过程不在此写出了, 我们只给出最后的结果为

\[ \rho_{1(23 \cdots p)}=\sqrt{1-|P| / P_{11}} \]

这里 $|P|$ 为 (4.10) 所定义的方阵 $P$ 的行列式, $P_{11}$ 如前, 是方阵 $P$ 的 $(1,1)$ 元的子式.

如果对 $\left(X_{1}, X_{2}, \cdots, X_{p}\right)$ 进行了 $n$ 次观察, 得样本 $\left(X_{1 i}, X_{2 i}\right.$, $\left.X_{p i}\right), i=1, \cdots, n$, 则由之计算出样本相关阵 R(见 (4.12) 式), 以 $R$ 取代 (4.16)中之 $P$, 得样本复相关系数

\[ r_{1(23 \cdots p)}=\sqrt{1-|R| / R_{11}} \]

它可作为 $\rho_{1(23 \cdots p)}$ 的估计.

关于复相关系数的检验, 实用上有兴趣的是

\[ H_{0}: \rho_{1(23 \cdots p)}=0 \]

直观上看,一个显然的检验方法是

\[ \text { 当 } r_{1(23 \cdots p)} \leqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

要依据检验水平 $\alpha$ 去决定 (4.19) 中的常数 $C$, 就必须求出当 $H_{0}$ 成立时, $r_{1(23 \cdots p)}$ 的分布. 可以证明: 当正态假定成立且 $H_{0}$ 为真时, $r_{1(23 \cdots p)}^{2}$ 的分布为所谓 “ $\beta$ 分布”, 其密度函数 $f(x)$ 为

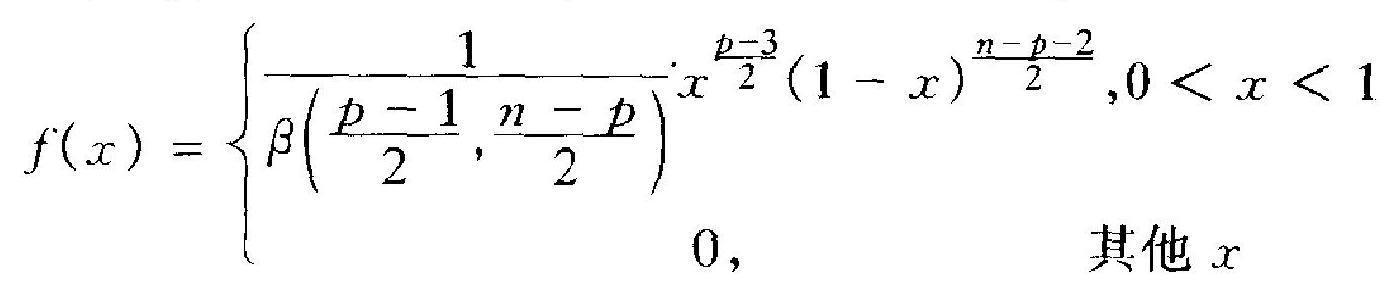
其中 $\beta\left(\frac{p-1}{2}, \frac{n-p}{2}\right)$ 曾在第二章的附录中定义过. 用这个分布去决定 (4.19) 中的 $C$, 可以通过 $F$ 分布表. 因为, 在 (4.20) 的基础上可以证明: 在 $H_{0}$ 成立时有

\[ \frac{n=p}{p-1} \frac{r_{1(23 \cdots p)}^{2}}{1-r_{1(23 \cdots p)}^{2}} \sim F_{(p-1) / 2,(n-p) / 2} \]

$F_{a, b}$ 为自由度 $a, b$ 的 $F$ 分布 (见第 2 章例 4.11). 由 (4.21), 定出在给定水平 $\alpha$ 时, (4.19) 式中的 $C$ 为

$C=$

\[ \left[\left(\frac{p-1}{n-p} F_{(p-1) / 2,(n-p) / 2}(\alpha)\right) /\left(1+\frac{p-1}{n-p} F_{(p-1) / 2,(n-p) / 2}(\alpha)\right)\right]^{1 / 2} \]

在以上的叙述中, $X_{1}, \cdots, X_{p}$ 也可以只是考察的全部变量中的一部分. 例如, $X_{1}$ 代表亩产量, $X_{2}, \cdots, X_{p}$ 代表所考察的全部气象因子, 如有关各月的降水量, 月平均气温等, 而 $X_{p+1}, \cdots, X_{q}$ 等则代表与田间管理有关的因子, 另外还可以有别的因子. 我们可以考虑 $X_{1}$ 与 $\left(X_{2}, \cdots, X_{p}\right)$ 的复相关, 以看看亩产量与气象因子相关的程度如何, 可以考虑 $X_{1}$ 与 $\left(X_{p+1}, \cdots, X_{q}\right)$ 的复相关, 以看看亩产量与管理因子相关的程度如何, 等等. 上面所说的估计和检验方法当然仍然适用.

6.4 相关分析⚓︎

评论