7.3.3 公平性
公平分配的目标是计算出满足所需的公平标准的分配。如前文所述,自早期的公平分配文献以来,主要有两个公平性概念,即“无嫉妒”和“比例公平”。
如果没有参与者认为另一个参与者得到了更好的分配,那么就可 以说这种分配是“无嫉妒”的。“无嫉妒”取决于参与者彼此之间的比较。
对参与人𝑖, 𝑗,有𝑉𝑖(𝐴𝑖) ≥ 𝑉𝑖(𝐴𝑗) 。
另一方面,如果每个参与者都能保证自己在总价值中占有一定比例的份额,而与其他人的所得无关,那么这种分配就被称为比例公平
分配。
定义 4(比例公平)一个分配是比例公平(PROP)的,如果对每个参与人都有𝑉𝑖(𝐴𝑖) ≥ 𝑉𝑖(𝑀) / 𝑁。
根据定义易得如果一个分配是无嫉妒的,那么这个分配也是比例公平的,反之则不然。通过例 1 我们可以更好的理解无嫉妒分配和比例公平分配。
者对不同物品的估值如表 1。

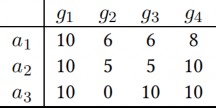
表 3-1:例 1 中参与者对不同物品的估值。其中,第 i 行,第 j 列的值表示参与者𝒂𝒊对物品𝒈𝒋的估值
分配𝐴 = {𝐴1, 𝐴2, 𝐴3} 是无嫉妒的,其中𝐴1 = {𝑔2, 𝑔3}, 𝐴2 =
{𝑔4}, 𝐴3 = {𝑔1}。参与者 1 不会嫉妒, 因为𝑉1(𝐴1) = 12 >
𝑉1(𝐴2) = 8 > 𝑉1(𝐴2) = 10 。 参与者 2 不会嫉妒, 因为
𝑉2(𝐴2) = 𝑉2(𝐴1) = 𝑉2(𝐴3) = 10。参与者 3 也不会嫉妒,因为,
𝑉3(𝐴3) = 𝑉3(𝐴1) = 𝑉3(𝐴2) = 10。所以分配 A 是无嫉妒分配。
尽管例 1 中存在无嫉妒分配,但在分配不可分割的物品时,无嫉妒和比例公平分配并不总是存在。最简单的例子是两个参与者和一个单一物品的情况,两个参与者都希望得到该物品。但由于只有一个参与者最终能得到该物品,另一个参与者得到的价值为零,他就会嫉妒得到了该物品的参与者,并且他也没有得到他应得的份额。尽管不可
分割的物品的公平分配存在这种不可能性,我们仍然有兴趣关注无嫉妒或者比例公平分配是否存在。不幸的是,事实证明,即使是判断一个实例是否存在无嫉妒或比例公平分配的问题都是 NPC 的[Lipton等人][10] 。因此对于不可分割的物品,我们对上述两个概念进行了多种松弛定义。
N,都有: ∃𝑔 ∈ 𝐴𝑗, 𝑉𝑖(𝐴𝑖) ≥ 𝑉𝑖 (𝐴𝑗\{𝑔})。
例 2 为了方便理解 EF1 以及后续相关的定义,我们考虑一个有
3 个参与者和 5 个不可分割的物品的简单例子。每个参与者对不同物
品的估值如表 2:
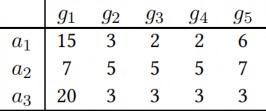
表 3-2:例 2,例 3,例 4 的估值表
在例 2 中不存在任何“无嫉妒”或“比例公平”分配。因为在任何比例公平分配中,参与者𝑎3 必须至少得到 {𝑔1} 或 {𝑔2, 𝑔3, 𝑔4 , 𝑔5}。在后一种情况下,𝑎1和𝑎2中至少有一个会得不到任何物品。而在前一种情况下,𝑎1必须至少得到其余四种商品中的三种,𝑎2必须至少得到两种,这是不可能的。另一方面,我们发现分配𝐴1 = {𝑔3, 𝑔4},𝐴2 =
{𝑔2, 𝑔5},𝐴3 = {𝑔1}是 EF1 的分配:𝑎2和𝑎3并不嫉妒其他参与者,而且𝑎1对𝑎2和𝑎3的嫉妒可以通过移除来消除。分别从𝐴2中删除𝑔5、从𝐴3中删除𝑔1,就可以消除𝑎1对𝑎2和𝑎3的嫉妒。
通过例 2 我们可以看到,EF1 条件即使在参与者的估值函数是单调的情况下(参与者们对物品的偏好序列是相同的)也是很容易就能实现的。事实上,在很多情况下 EF1 是一个非常弱的公平的概念。因为在与另一个参与者做比较时即使被移除掉的是价值很高的物品(例
如,房子,车子),我们仍然认为公平。例如,在例 2 中,从𝑎1的视角来看,想要达到 EF1 的要求,𝑎1需要移除估值很高的物品才能实现不嫉妒其他参与者。这一结果看起来似乎并不公平。因此,需要一个约束更强的更加公平的评判标准来判断分配是否公平。
与者𝑖,𝑗 ∈ N,都有: ∀𝑔 ∈ 𝐴𝑗, 𝑉𝑖(𝐴𝑖) ≥ 𝑉𝑖(𝐴𝑗\{𝑔})。
例 3 回顾在例 2 中得到的分配𝐴1 = {𝑔3, 𝑔4},𝐴2 = {𝑔2,𝑔5},
𝐴3 = {𝑔1}。这个分配不是一个 EFX 的分配。因为即使𝑎2除掉𝑔2, 𝑎1
仍然会嫉妒 a2。不过,我们可以更改分配为 B1 = {𝑔4,𝑔5},B2 = {𝑔2,
𝑔3},B3 = {𝑔1}。在这种分配下,𝑎1对𝑎3的嫉妒可以通过从𝐵3中移除
𝑔1来消除,而𝑎2对𝑎1的嫉妒可以通过从𝐵1中移除𝑔4来消除。
与EF1 不同,EFX 分配的存在性是一个具有挑战性的开放问题。 Procaccia [11] 将其称为“公平分配最神秘的问题”。在过去几年中,一系列工作部分或近似地解决了这个问题。除了上述我们介绍过的 EF1和 EFX 两种松弛的公平分配的概念以外,离散的公平分配中一个被广泛研究的公平概念是最大最小共享公平(maximin share fairness),是由Budish[12] 提出的。这个概念可以看作是对著名的“分和选”方法原理的概括。这个概念确保了在最差情况下能保持的最好的分配。是对比例公平的松弛定义。
定义 7(MMS) 𝒜n(M)是把𝑀分给𝑛个参与者的所以可能的分配
的集合。分配 A 是 MMS 分配,如果对于∀𝑖 ∈ 𝑁, 有:
𝑉𝑖(𝐴𝑖) ≥ 𝜇𝑛(𝑀) = 𝑚𝑎𝑥 𝑚𝑖𝑛 𝑉𝑖(𝑆) 。
𝑖 𝐵 ∈𝒜𝑛(𝑀) 𝑆 ∈𝐵
例 4 我们回顾例 2,例 3 得到的两个分配。通过表 2,可以得到:
𝜇3(𝑀) = 6,𝜇3(𝑀) = 7,𝜇3(𝑀) = 6。因此 B1 = {𝑔4,𝑔5},B2
1 2 3
= {𝑔2,𝑔3},B3 = {𝑔1}。是 MMS 分配。而𝐴1 = {𝑔3, 𝑔4},𝐴2 = {𝑔2,
𝑔5},𝐴3 = {𝑔1}并不是 MMS 分配。因为𝑉1(𝐴1) = 4 < 6, 因此例
2 的分配不是 MMS 分配。
计算 MMS 分配,甚至计算一个参与者的最差情况下的最好份额都是 NP-hard 问题。自 MMS 分配概念提出以来,它的存在一直是一个非常有趣的开放性问题。Kurokawa 等人[2018, 2016][13] -[14] 最终给出了否定的答案,他们证明了当存在两个以上参与者时,MMS 分配并不总是存在。不过可以计算近似的 MMS 分配。