答案⚓︎

习题提示与解答⚓︎

1. 第一章⚓︎

B.
一种可能的表法是

\[ \begin{aligned} A_{1} & +\cdots+A_{n}=A_{1}+\left(A_{2}-A_{1}\right)+\left[A_{3}-\left(A_{1}+A_{2}\right)\right] \\ & +\cdots+\left[A_{n}-\left(A_{1}+\cdots+\cdots A_{n-1}\right)\right] \end{aligned} \]

先把 \(A+B+C\) 表为互斥事件和:

\[ A+B+C=A+(B-A B)+(C-A C-\bar{A} B C) \]

再证明 \(P(B-A B)=P(B)-P(A B), P(C-A C-\bar{A} B C)=\) \(P(C)-P(A C)-P(\bar{A} B C)\), 及 \(P(\bar{A} B C)=P(B C)-P(A B C)\), 整理即得。

充要条件是 \(P(A), P(B)\) 中至少有一个为 0 .
不一定. 成立的充要条件是 \(P(B-A)=0\).

8 . 反复利用以下两个重要公式

\[ \overline{A_{1} A_{2} \cdots A_{n}}=\sum_{i=1}^{n} \bar{A}_{i}, \overline{A_{1}+A_{2}+\cdots+A_{n}}=\prod_{i=1}^{n} \bar{A}_{i} \]

（这两公式请自证一下）

考虑一个盒子内含有三个球, 其上分别标有数字 1,2 , 3. 现从中随机抽出一个, 记事件

\(A=\{\) 抽出 1 或 2 球 \(\}, B=\) 抽出 2 球 \(\}, C=\{\) 抽出 2 或 3 球 \(\}\)

第一问: 直接计算 \(P(C(A+B))=P(C A)+P(C B)\). 第二问: 仍算 \(P(C(A+B))\), 但把 \(A+B\) 表为 \(A+B=(A-B)+\) \(A B+(B-A)\). 设法去证明

\[ \begin{aligned} & P(C(A-B))=P(C) P(A-B) \\ & P(C(B-A))=P(C) P(B-A) \end{aligned} \]

前一式可由 \(P(C A)=P(C) P(A), P(C \cdot A B)=P(C) P(A B)\) 两边相减得到, 因 \(C A-C A B=C(A-A B)=C(A-B)\), 及 \(P(A-\) \(B)=P(A)-P(A B)\).

例: 一盒中有 12 个球, 分别标有数字 \(1,2, \cdots, 12\). 现从其中随机抽出一个, 定义事件

\(A=\) 抽出 \(1,2,3\) 号球之一 \(\}, B=\) 抽出 \(2,3,4\) 号球之一 \(\}\)

\[ C=\{\text { 抽出 } 2,3,5,6,7,8,9,10 \text { 号球之一 }\} \text {. } \]

前一部分的证明与第 10 题的第二问类似, 反例可用 11 题的例子.
\(A=A_{1}\left(A_{2}+A_{3}\right)\left(A_{4} A_{5}+A_{5} A_{6}+A_{4} A_{6}\right)\) 用乘法定理, 注意

\[ \begin{aligned} & P\left(\overline{\left.A_{4} A_{5}+\overline{A_{5} A_{6}+A_{4} A_{6}}\right)}=P\left(\bar{A}_{4} \bar{A}_{5} \bar{A}_{6}\right)+P\left(A_{4} \bar{A}_{5} \bar{A}_{6}\right)\right. \\ & +P\left(\bar{A}_{4} A_{5} \bar{A}_{6}\right)+P\left(\bar{A}_{4} \bar{A}_{5} A_{6}\right) \end{aligned} \]

逐项用乘法定理,答案: \(320 / 729=0.439\).

反例: 一盒中有 5 个球, 分别标上数字 \(1,2, \cdots, 5\). 现从中随机抽出一个, 定义事件

\[ \begin{gathered} A=\text { 抽出 } 1 \text { 或 } 2 \text { 球 }\}, B=\{\text { 抽出 } 2 \text { 或 } 3 \text { 球 }\}, \\ C=\{\text { 抽出 } 1 \text { 或 } 3 \text { 球 }\} \end{gathered} \]

需要证明

\[ P\left(B_{i_{1}} B_{i_{2}} \cdots B_{i_{r}}\right)=P\left(B_{i_{1}}\right) P\left(B_{i_{2}}\right) \cdots P\left(B_{i_{r}}\right) \]

对任何满足条件 \(2 \leqslant r \leqslant n\) 的 \(r\) 及 \(1 \leqslant i_{1}<i_{2}<\cdots<i_{r} \leqslant n\). 以 \(k\) 记 \(B_{i}, \cdots, B_{i_{r}}\) 中 \(B_{i j}=\bar{A}_{i_{j}}\) 的 \(j\) 的个数. 对 \(k\) 实行归纳法. 若 \(k=0\), 则由独立性定义知 (1) 式对, 现设 \(k=m\) 时(1) 式对. 来证明当 \(k=m+\) 1 时 (1) 式也对. \(B_{i_{1}}, \cdots, B_{i_{r}}\) 中有 \(m+1\) 个有 “bar”的. 为方便计且不失普遍性, 不妨设 \(B_{i_{1}}=\bar{A}_{i_{1}}\). 有

\[ B_{i_{2}} B_{i_{3}} \cdots B_{i_{r}}=B_{i_{1}} B_{i_{2}} \cdots B_{i_{r}}+A_{i_{1}} B_{i_{2}} \cdots B_{i_{r}} \]

右边两事件互斥, 故

\[ P\left(B_{i_{1}} \cdots B_{i_{r}}\right)=P\left(B_{i_{2}} \cdots B_{i_{r}}\right)-P\left(A_{i_{1}} B_{i_{2}} \cdots B_{i_{r}}\right) \]

因为在 \(B_{i_{2}}, \cdots, B_{i_{r}}\) 中只有 \(m\) 个加 “bar” 的, \(A_{i_{1}}, B_{i_{2}}, \cdots, B_{i_{r}}\) 中也只有 \(m\) 个加 “bar”的. 故由归纳假设, 知

\[ \begin{gathered} P\left(B_{i_{2}} \cdots B_{i_{r}}\right)=P\left(B_{i_{2}}\right) \cdots P\left(B_{i_{r}}\right), \\ P\left(A_{i_{1}} B_{i_{2}} \cdots B_{i_{r}}\right)=P\left(A_{i_{1}}\right) P\left(B_{i_{2}}\right) \cdots P\left(B_{i_{r}}\right) \end{gathered} \]

以此代人 (2)式, 并注意 \(1-P\left(A_{i_{1}}\right)=P\left(\bar{A}_{i_{1}}\right)=P\left(B_{i_{1}}\right)\), 得

\[ P\left(B_{i_{1}} \cdots B_{i_{r}}\right)=P\left(B_{i_{1}}\right) \cdots P\left(B_{i_{r}}\right) \]

于是完成了归纳证明.

总排列数为 \(4 !=24\). 分别计算放对 \(1,2,4\) 封的排列数为 8,6 和 1. 答案 \(: 9 / 24=3 / 8\).
用全概率公式, 对丙而言, 分四种情况: \(A_{1}=\{\) 甲抽中, 乙抽中 \(\}, A_{2}=\{\) 甲中乙不中 \(\}, A_{3}=\{\) 甲不中乙中 \(\}, A_{4}=\{\) 甲、乙都不中}. 答案: \(2 / 10,17 / 55,41 / 110\). 以丙抽中的可能性最大.
\((n !)^{p} / \frac{(n p) !}{(p !)^{n}}=(n !)^{p}(p !)^{n} /(n p) !\)
再继续赌四局, 排出一切可能情况, 答案为 \(11: 5\).
答案为 \(30 / 91\). 其所以不同, 原因在于, 仔细一想可知 : 知道某特定骰子出么, 比知道至少出一个么, 要更有利于多出么, 因而更不利于得出大的和数.
由对称性考虑, 可让选定的一男孩固定一个位置.剩下的 \(n+m-1\) 个小孩归结到直线排列的情况.
第一个事件的对立事件为“每方各有一张 \(A\) ”. 其概率为 \(4 ! \frac{48 !}{(12 !)^{4}} / \frac{(52) !}{(13 !)^{4}}\). 后一事件比较复杂, 要分解为一些互斥事件之和, 即如

东方 \(2 A\),西、南各 \(1 A\}\) 等,共有 \(4 \times 3=12\) 种;

㑈,西方各 \(2 A\}\) 等,共有 6 种.

前一事件概率为 \(4 !\left(\begin{array}{l}4 \\ 2\end{array}\right) \frac{48 !}{11 !(12 !)^{2} 13 !} / \frac{52 !}{(13 !)^{4}}\), 后一事件的概率为 \(\left(\begin{array}{l}4 \\ 2\end{array}\right) \cdot\left(\begin{array}{l}4 \\ 2\end{array}\right) \cdot \frac{48 !}{(11 !)^{2}(13 !)^{2}} / \frac{52 !}{(13 !)^{4}}\), 答案 : 0.719135654 .

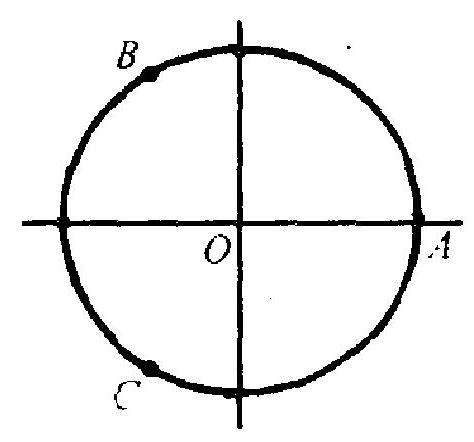
最简单的做法如下: 从对称考虑出发,不妨把甲取的点定在图 1 中的 \(A\) 点处. 这时, 为了使题中所说的事件发生, 乙所选的点必须在图 1 中的 \(B A C\) 弧内, 且 \(\angle B O A\) 和 \(\angle C O A\) 都是 \(120^{\circ}\). 故概率为 \(2 / 3\).

类 1

做法大体上类似例 2.5 . 答案为

\[ \frac{7 !}{2 ! 1 ! 1 ! 3 !} \cdot \frac{8 !}{2 ! 2 ! 3 ! 1 !} / 7^{8}=0.1224 \text {. } \]

(a) 所求概率为 \(\left(1-p_{1}\right) \cdots(1-\) \(p_{n}\) ). 利用 \(1-x<\mathrm{e}^{-x}\) 当 \(x>0\). (b) 所求概率不超过 \(\sum^{*} p_{i 1} \cdots p_{i k}, \sum^{*}\) 求和的范围为 \(1 \leqslant i_{1}<\cdots<i_{k} \leqslant n\) 但在 \(\left(p_{1}+\right.\) \(\left.\cdots+p_{n}\right)^{k}\) 的展开式中, 每一个这样的项都出现 \(k\) !次.
不可以那样算, 理由与 21 题同.
甲胜概率为 (用全概率公式)

\[ p=\sum_{n=1}^{\infty} \frac{1}{2^{n}(n+1)} \]

不难证明 \(p<1 / 2\). 因为

\[ \begin{aligned} p & =\frac{1}{4}+\frac{1}{12}+\sum_{n=3}^{\infty} \frac{1}{2^{n}(n+1)}<\frac{1}{3}+\frac{1}{4} \sum_{n=3}^{\infty} \frac{1}{2^{n}} \\ & =\frac{1}{3}+\frac{1}{4} \cdot \frac{1}{4}<1 / 2 \end{aligned} \]

因此这规则对甲不利. ( \(p\) 的确值为 \(2 \log 2-1\), 试证明之.)

答案⚓︎

习题提示与解答⚓︎

1. 第一章⚓︎

评论