2.4 随机变量的函数的概率分布⚓︎

\title{ 2.4 随机变量的函数的概率分布 }

在理论和应用上, 经常碰到这种情况: 已知某个或某些随机变

82 - 量 \(X_{1}, \cdots, X_{n}\) 的分布, 现另有一些随机变量 \(Y_{1}, \cdots, Y_{m}\), 它们都是 \(X_{1}, \cdots, X_{m}\) 的函数:

\[ Y_{i}=g_{i}\left(X_{1}, \cdots, X_{n}\right), i=1, \cdots, m \]

要求 \(\left(Y_{1}, \cdots, Y_{m}\right)\) 的概率分布. 事实上我们已经考虑过这样的一个例子, 即例 3.6.

在数理统计学中常碰到这个问题. 在那里, \(X_{1}, \cdots, X_{n}\) 是原始的观察或试验数据, \(Y_{1}, \cdots, Y_{m}\) 则是为某种目的将这些数据“加工”而得的量, 称为 “统计量”. 例如, \(X_{1}, \cdots, X_{n}\) 可能是对某个末知量 \(a\) 作 \(n\) 次量测的结果, 量测有误差, 我们决定用 \(X_{1}, \cdots, X_{n}\) 的算术平均值 \(\bar{X}=\left(X_{1}+\cdots+X_{n}\right) / n\) 去估计末知量 \(a . \bar{X}\) 就是 \(X_{1}, \cdots\), \(X_{n}\) 的函数.

\subsection{1 离散型分布的情况}

这种情况比较简单, 故只鿒稍加解释. 例如, 变量 \(X\) 取 6 个值 \(-2,-1,0,1,2,3\), 其概率分别为 \(1 / 12,3 / 12,3 / 12,2 / 12,1 / 12\) 和 \(2 / 12\), 而 \(Y=X^{3}\). 则 \(Y\) 取 \(-8,-1,0,1,8,27\) 这 6 个值, 它们没有相重的, 故取这些值的概率, 就仍如上述.

但若考虑 \(Y=X^{2}\), 则情况有所不同. 相应于 \(X\) 的 6 个值的 \(Y\) 值分别为 \(4,1,0,1,4,9\), 其中有相重的. 相重值的概率需要合并起来:

\[ \begin{aligned} & P(Y=0)=P(X=0)=3 / 12 \\ & P(Y=1)=P(X=1)+P(X=-1)=2 / 12+3 / 12=5 / 12 \\ & P(Y=4)=P(X=2)+P(X=-2)=1 / 12+1 / 12=2 / 12 \\ & P(Y=9)=P(X=3)=2 / 12 \end{aligned} \]

一般情况在原则上也一样: 把 \(Y=g\left(X_{1}, \cdots, X_{n}\right)\) 可以取的不同值找出来, 把与某个值相应的全部 \(\left(X_{1}, \cdots, X_{n}\right)\) 值的概率加起来, 即得 \(Y\) 取这个值的概率. 当然, 在实际做的时候, 涉及的计算也可能并不简单.

例 4.1 设 \(\left(X_{1}, X_{2}, \cdots, X_{n}\right)\) 服从多项分布 \(M\left(N ; p_{1}, \cdots\right.\), \(\left.p_{n}\right), n \geqslant 3\). 试求 \(Y=X_{1}+X_{2}\) 的分布.

\(Y\) 取值为 \(0,1, \cdots, N\). 指定 \(k\), 有

\[ P(Y=k)=\sum^{\prime} \frac{N !}{k_{1} ! k_{2} ! k_{3} ! \cdots k_{n} !} p_{1}^{k_{1}} p_{2}^{k_{2}} p_{3}^{k_{3} \cdots} p_{n^{n}}^{k^{n}} \]

这里 \(\sum\) '表示求和的范围为

\[ k_{i} \text { 为非负整数, } k_{1}+k_{2}=k, k_{1}+\cdots+k_{n}=N \]

记 \(p_{i}^{\prime}=p /\left(1-p_{1}-p_{2}\right), i=3, \cdots, n\), 则 \(p_{3}^{\prime}+\cdots+p_{n}^{\prime}=1\). 将上式写为

\[ \begin{aligned} & P(Y=k)=\frac{N !}{k !(N-k) !}\left(1-p_{1}-p_{2}\right)^{N-k} \sum^{\prime \prime} \frac{k !}{k_{1} ! k_{2} !} p_{1}^{k_{1}} p_{2}^{k_{2}^{2}} \\ & \text { - } \sum \cdots \frac{(N-k) !}{k_{3} ! \cdots k_{n} !} p_{3}^{k_{3} \cdots} p_{n^{n}}^{k^{n}} \end{aligned} \]

这里 \(\sum^{\prime \prime}\) 求和的范围为: \(k_{1}, k_{2}\) 为非负整数, \(k_{1}+k_{2}=k . \sum^{\prime \prime \prime}\) 求和的范围为; \(k_{3}, \cdots, k_{n}\) 为非负整数, \(k_{3}+\cdots+k_{n}=N-k\). 由于 \(p_{3}^{\prime}+\cdots+p_{n}^{\prime}=1\). 由 (2.4) 式知 \(\sum '\) '”这个和的值是 \(1 . \sum^{\prime \prime}\) 这个和的值为 \(\left(p_{1}+p_{2}\right)^{k}\). 于是得到

\[ \begin{aligned} P(Y=k) & =\frac{N !}{k !(N-k) !}\left(p_{1}+p_{2}\right)^{k}\left[1-\left(p_{1}+p_{2}\right)\right]^{N-k} \\ & =b\left(k ; N, p_{1}+p_{2}\right) \end{aligned} \]

即 \(Y\) 服从二项分布 \(B\left(N, p_{1}+p_{2}\right)\).

如果从概率意义的角度去考虑, 这个结果不用计算就可以知道: 在定义多项分布时有 \(n\) 个事件 \(A_{1}, A_{2}, A_{3}, \cdots, A_{n} . X_{1}, X_{2}\), \(X_{3}, \cdots, X_{n}\) 分别是它们在 \(N\) 次试验中发生的次数. 现若记 \(A=A_{1}\) \(+A_{2}\), 则事件 \(A, A_{3}, \cdots, A_{n}\) 仍构成一个完备事件群, 其概率分别为 \(p_{1}+p_{2}, p_{3}, \cdots, p_{n}\). 记 \(Y=X_{1}+X_{2}\), 则 \(\left(Y, X_{3}, \cdots, X_{n}\right)\) 构成多项分布 \(M\left(N ; p_{1}+p_{2}, p_{3}, \cdots, p_{n}\right)\), 而 \(Y\) 成为这个多项分布的一个边缘分布. 于是按例 2.7 即得出上述结论.

这就是我们前面几个地方曾提及的概率思维. 概率论中有不少结果可以用纯分析方法证明, 但如利用概率思维, 有时证明可以简化, 学习概率论的一个要素在于锻炼这种概率思维. 例 4.2 设 \(X_{1}\) 和 \(X_{2}\) 独立, 分别服从二项分布 \(B\left(n_{1}, p\right)\) 和 \(B\) \(\left(n_{2}, p\right)\) (注意 \(p\) 是公共的), 求 \(Y=X_{1}+X_{2}\) 的分布.

\(Y\) 之可能值为 \(0,1, \cdots, n_{1}+n_{2}\). 固定 \(k\) 于上述范围内, 由独立性假定, 有

\[ \begin{aligned} P(Y=k) & =\sum^{\prime} P\left(X_{1}=k_{1}, X_{2}=k_{2}\right) \\ & =\sum^{\prime}\left(\begin{array}{l} n_{1} \\ k_{1} \end{array}\right) p^{k_{1}}(1-p)^{n_{1}-k_{1}}\left(\begin{array}{l} n_{2} \\ k_{2} \end{array}\right) p^{k_{2}}(1-p)^{n_{2}-k_{2}} \\ & =\sum^{\prime}\left(\begin{array}{l} n_{1} \\ k_{1} \end{array}\right)\left(\begin{array}{l} n_{2} \\ k_{2} \end{array}\right) p^{k}(1-p)^{n_{1}+n_{2}-k} \end{aligned} \]

此处 \(\sum\) '求和的范围为: \(k_{1}, k_{2}\) 为非负整数, \(k_{1}+k_{2}=k\). 按第一章公式 (2.5), 得 \(\sum,\left(\begin{array}{l}n_{1} \\ k_{1}\end{array}\right)\left(\begin{array}{l}n_{2} \\ k_{2}\end{array}\right)=\left(\begin{array}{c}n_{1}+n_{2} \\ k\end{array}\right)\), 于是

\[ P(Y=k)=\left(\begin{array}{c} n_{1}+n_{2} \\ k \end{array}\right) p^{k}(1-p)^{n_{1}+n_{2}-k}=b\left(k ; n_{1}+n_{2}, p\right) \]

即 \(Y\) 服从二项分布 \(B\left(n_{1}+n_{2}, p\right)\). 这个结果很容易推广到多个的情形: 若 \(X_{i} \sim B\left(n_{i}, p\right), i=1, \cdots, m\), 而 \(X_{1}, \cdots, X_{m}\) 独立, 则 \(X_{1}\) \(+\cdots+X_{m} \sim B\left(n_{1}+\cdots+n_{m}, p\right)\). 证明不难用归纳法作出, 细节留给读者.

上述结论如用“概率思维”, 则不证自明:按二项分布的定义，若 \(X \sim B(n, p)\), 则 \(X\) 是在 \(n\) 次独立试验中事件 \(A\) 出现的次数, 而在每次试验中 \(A\) 的概率保持为 \(p\). 今 \(X_{i}\) 是在 \(n_{i}\) 次试验中 \(A\) 出现的次数, 每次试验 \(A\) 出现的概率为 \(p\). 故 \(Y=X_{1}+\cdots+X_{m}\) 是在 \(n_{1}+\cdots+n_{m}\) 次独立试验中, \(A\) 出现的次数, 而在每次试验中 \(A\) 出现的概率保持为 \(p\). 故按定义即得 \(Y \sim B\left(n_{1}+\cdots+n_{m}, p\right)\).

例 4.3 设 \(X_{1}, X_{2}\) 独立, 分别服从波哇松分布 \(P\left(\lambda_{1}\right)\) 和 \(P\left(\lambda_{2}\right)\) (见例 1.2). 证明: \(Y=X_{1}+X_{2}\) 服从波哇松分布 \(P\left(\lambda_{1}+\right.\) \(\left.\lambda_{2}\right)\).

\(Y\) 的可能值仍为一切非负整数. 固定这样一个 \(k\), 则由独立性假定及波哇松分布的形式 (1.7), 有

\[ \begin{aligned} P(Y=k) & =\sum ' P\left(X_{1}=k_{1}, X_{2}=k_{2}\right) \\ & =\sum ' P\left(X_{1}=k_{1}\right) P\left(X_{2}=k_{2}\right) \\ & =\sum ' \mathrm{e}^{-\lambda_{1}} \lambda_{1}^{k_{1} / k_{1}} ! \cdot \mathrm{e}^{-\lambda_{2}} \lambda_{2}^{k^{2} / k_{2}} ! \\ & =\mathrm{e}^{-\left(\lambda_{1}+\lambda_{2}\right) / k ! \sum \prime} \frac{k !}{k_{1} ! k_{2} !} \lambda_{1}^{k_{1}} \lambda_{2}^{k^{2}} \end{aligned} \]

这里 \(\sum '\) 的求和范围与上例相同, 因而这个和等于 \(\left(\lambda_{1}+\lambda_{2}\right)^{k}\). 故

\[ P(Y=k)=\mathrm{e}^{-\left(\lambda_{1}+\lambda_{2}\right)}\left(\lambda_{1}+\lambda_{2}\right)^{k} / k ! \]

因而证明了所要的结果. 这结果也自然地可推广到多个的情形.

在例 1.2 后面我们对波哇松分布通过二项分布而产生的过程作了一个解释, 利用这个解释的架构, 不须计算即可容易看出这个结论.我们留给读者自己去完成. 这样解释的目的,倒不在于为了避免计算 (就本例而言, 计算很简单, 可能比通过上述解释还简便些), 而是它使人了解为什么会有这个结果 (前面几个例子也如此). 形式的计算使人相信结果是对的,但不能提供直观上的启发性.

\subsection{2 连续型分布的情况:一般讨论}

本节的其余部分将讨论更有兴趣的连续型情况. 这一段对处理这种问题的一般方法作些介绍,然后在 2.4.3,2.4.4 两段中,分别对两个在数理统计学上重要的情况专门进行讨论, 并由此引出在数理统计学上几个重要的概率分布.

先考虑一个变量的情况. 设 \(X\) 有密度函数 \(f(x)\). 设 \(Y=\) \(g(x), g\) 是一个严格上升的函数, 即当 \(x_{1}<x_{2}\) 时, 必有 \(g\left(x_{1}\right)<\) \(g\left(x_{2}\right)\). 又设 \(g\) 的导数 \(g^{\prime}\) 存在. 由于 \(g\) 的严格上升性, 其反函数 \(X\) \(=h(Y)\) 存在且 \(h\) 的导数 \(h^{\prime}\) 也存在.

任取实数 \(y\). 因 \(\mathrm{g}\) 严格上升,有

\(P(Y \leqslant y)=P(g(X)) \leqslant y)=P(X \leqslant h(y))=\int_{-\infty}^{h(y)} f(t) \mathrm{d} t\)

\(Y\) 的密度函数 \(l(y)\), 即是这个表达式对 \(y\) 求导数（见定义 1.3). 有

\[ l(y)=f(h(y)) h^{\prime}(y) \]

如果 \(Y=g(X)\) 而 \(g\) 是严格下降, 则 \(\{g(X) \leqslant y\}\) 相当于 \(\{X \geqslant h(Y)\}\). 于是

\[ P(Y \leqslant y)=P(g(X) \leqslant y)=P(X \geqslant h(y))=\int_{h(y)}^{\infty} f(t) \mathrm{d} t \]

对 \(y\) 求导数, 得 \(Y\) 的密度函数

\[ l(y)=-f(h(y)) h^{\prime}(y) \]

因为当 \(g\) 严格下降时, 其反函数 \(h\) 也严格下降, 故 \(h^{\prime}(y)<0\). 这样 \(l(y)\) 仍为非负的. 总结 (4.2), (4.3) 两式, 得知在 \(g\) 严格单调 (上升下降都可以) 的情况下, 总有 \(g(X)\) 的密度函数 \(l(y)\) 为

\[ l(y)=f(h(y))\left|h^{\prime}(y)\right| \]

例 4.4 \(Y=a X+b, a \neq 0\). 反函数为 \(X=(Y-b) / a\). 由 (4.4) 得出: \(a X+b\) 的密度函数为

\[ l(y)=f((y-b) / a) /|a| \]

若 \(X\) 有正态分布 \(N\left(\mu, \sigma^{2}\right)\), 则据正态密度函数的表达式 (1.14) 和公式 (4.5), 易算出 \(a X+b\) 服从正态分布 \(N\left(a \mu+b, a^{2} \sigma^{2}\right)\). 特别, 当 \(Y=(X-\mu) / \sigma\) 时, 有 \(Y \sim N(0,1)\). 这一点在例 1.6 中已指出过了.

当 \(Y=g(X)\) 而 \(g\) 不为严格单调时,情况复杂一些,但并无原则困难. 我们不去考虑一般情况, 而只注意一个特例 \(Y=X^{2}\). 仍以 \(f\) 记 \(X\) 的概率密度. 因 \(Y\) 非负, 有 \(P(Y \leqslant y)=0\) 当 \(y \leqslant 0\). 若 \(y>\) 0 , 则有

\[ \begin{aligned} P(Y \leqslant y) & =P\left(X^{2} \leqslant y\right)=P(-\sqrt{y} \leqslant X \leqslant \sqrt{y}) \\ & =\int_{-\sqrt{y}}^{\sqrt{y}} f(t) \mathrm{d} t \end{aligned} \]

对 \(y\) 求导数, 得 \(Y\) 的密度函数 \(l(y)\) 为

\[ l(y)=\frac{1}{2} y^{-1 / 2}[f(\sqrt{y})+f(-\sqrt{y})] \text {, 当 } y>0 \]

而当 \(y \leqslant 0\) 时 \(l(y)=0\). 下面的特例很重要. 例 4.5 若 \(X \sim N(0,1)\), 试求 \(Y=X^{2}\) 的密度函数.

\[ \begin{aligned} & \text { 以 } f(x)=(\sqrt{2 \pi})^{-1} \mathrm{e}^{-x^{2} / 2} \text { 代人上式,得 } \\ & l(y)=(\sqrt{2 \pi y})^{-1} \mathrm{e}^{-y / 2} \text {, 当 } y>0 . l(y)=0 \text { 当 } y \leqslant 0 \end{aligned} \]

现在考虑多个变量的函数的情况, 以两个为例. 设 \(\left(X_{1}, X_{2}\right)\) 的密度函数为 \(f\left(x_{1}, x_{2}\right), Y_{1}, Y_{2}\) 都是 \(\left(X_{1}, X_{2}\right)\) 的函数:

\[ Y_{1}=g_{1}\left(X_{1}, X_{2}\right), Y_{2}=g_{2}\left(X_{1}, X_{2}\right) \]

要求 \(\left(Y_{1}, Y_{2}\right)\) 的概率密度函数 \(l\left(y_{1}, y_{2}\right)\). 在此, 我们要假定 (4.7) 是 \(\left(X_{1}, X_{2}\right)\) 到 \(\left(Y_{1}, Y_{2}\right)\) 的一一对应变换, 因而有逆变换

\[ X_{1}=h_{1}\left(Y_{1}, Y_{2}\right), X_{2}=h_{2}\left(Y_{1}, Y_{2}\right) \]

又假定 \(g_{1}, g_{2}\) 都有一阶连续偏导数. 这时, 逆变换 (4.8) 的函数 \(h_{1}, h_{2}\) 也有一阶连续偏导数, 且在一一对应变换的假定下, 贾可比行列式

\[ J\left(y_{1}, y_{2}\right)=\left|\begin{array}{ll} \partial h_{1} / \partial y_{1} & \partial h_{1} / \partial y_{2} \\ \partial h_{2} / \partial y_{1} & \partial h_{2} / \partial y_{2} \end{array}\right| \]

不为 0 .

现在我们在 \(\left(Y_{1}, Y_{2}\right)\) 的平面上任取一个区域 \(A\). 在变换 (4.8)之下, 这区域变到 \(\left(X_{1}, X_{2}\right)\) 平面上的区域 \(B\). 就是说, 事件 \(\left\{\left(Y_{1}, Y_{2}\right) \in A\right\}\) 等于事件 \(\left\{\left(X_{1}, X_{2}\right) \in B\right\}\). 考虑到 \(f\) 是 \(\left(X_{1}, X_{2}\right)\) 的密度函数, 有

\[ P\left(\left(Y_{1}, Y_{2}\right) \in A\right)=P\left(\left(X_{1}, X_{2}\right) \in B\right)=\iint_{B} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \]

使用重积分变数代换的公式, 在变换 (4.8)之下, 上式最右端一项的重积分变换为

\[ \begin{aligned} P\left(\left(Y_{1}, Y_{2}\right) \in A\right)= & \iint_{A} f\left(h_{1}\left(y_{1}, y_{2}\right), h_{2}\left(y_{1}, y_{2}\right)\right) \\ & \cdot\left|J\left(y_{1}, y_{2}\right)\right| \mathrm{d} y_{1} \mathrm{~d} y_{2} \end{aligned} \]

此式对 \(\left(Y_{1}, Y_{2}\right)\) 平面上任何区域 \(A\) 都成立. 于是, 按定义 2.2 (见 \((2.5)\) 式 \())\), 即得 \(\left(Y_{1}, Y_{2}\right)\) 的密度函数为

\[ l\left(y_{1}, y_{2}\right)=f\left(h_{1}\left(y_{1}, y_{2}\right), h_{2}\left(y_{1}, y_{2}\right)\right)\left|J\left(y_{1}, y_{2}\right)\right| \]

一个重要的特例是线性变换

\[ Y_{1}=a_{11} X_{1}+a_{12} X_{2}, Y_{2}=a_{21} Z_{1}+a_{22} X_{2} \]

假定变换的行列式 \(a_{11} a_{22}-a_{12} a_{21} \neq 0\), 则逆变换 (4.8) 存在且仍为线性变换:

\[ X_{1}=b_{11} Y_{1}+b_{12} Y_{2}, X_{2}=b_{21} Y_{1}+b_{22} Y_{2} \]

此变换的贾可比行列式为常数:

\[ J\left(y_{1}, y_{2}\right)=J=b_{11} b_{22}-b_{12} b_{21}=\left(a_{11} a_{22}-a_{12} a_{21}\right)^{-1} \]

按 (4.11) 式, 得出 \(\left(Y_{1}, Y_{2}\right)\) 的密度函数为

\[ l\left(y_{1}, y_{2}\right)=f\left(b_{11} y_{1}+b_{12} y_{2}, b_{21} y_{1}+b_{22} y_{2}\right)\left|b_{11} b_{22}-b_{12} b_{21}\right| \]

例 4.6 再回过头来考虑例 3.6. 为与此处记号一致, 把该例中的 \(R\) 和 \(\Theta\) 分别记为 \(Y_{1}, Y_{2}\), 这时逆变换 (4.8) 为

\[ X_{1}=Y_{1} \cos Y_{2}, X_{2}=Y_{1} \sin Y_{2} \]

贾可比行列式为

\[ J\left(y_{1}, y_{2}\right)=\left|\begin{array}{cc} \cos y_{2} & -y_{1} \sin y_{2} \\ \sin y_{2} & y_{1} \cos y_{2} \end{array}\right|=y_{1} \]

因为 \(\left(X_{1}, X_{2}\right)\) 的密度函数为

\[ f\left(x_{1}, x_{2}\right)=\frac{1}{2 \pi} \exp \left[-\frac{1}{2}\left(x_{1}^{2}+x_{2}^{2}\right)\right] \]

而 \(x_{1}^{2}+x_{2}^{2}=y_{1}^{2} \cos ^{2} y_{2}+y_{1}^{2} \sin ^{2} y_{2}=y_{1}^{2}\), 由公式 \((4.11)\), 得 \(\left(Y_{1}, Y_{2}\right)\) 的概率密度函数为 \(\frac{1}{2 \pi} \mathrm{e}^{-y_{1}^{2} / 2} y_{1}\). 变量范围为 \(0 \leqslant y_{1}<\infty, 0 \leqslant y_{2}<\) \(2 \pi\). 在这个范围之外为 0 . 这与例 3.6 中求出的一致.

本例还提醒了我们一点:必须注意变换以后变量的范围. 光从公式 (4.11) 上有时并不能看清这一点. 在本例中, 因为 \(\left(Y_{1}, Y_{2}\right)\) 是点的极坐标, 其范围易于判定, 在有些例子中, 则需经过一定的判断. 看下面的例子.

例 4.7 设 \(X_{1}, X_{2}\) 独立, 都服从指数分布 (1.20), 其中 \(\lambda=1\). 而设 \(Y_{1}=X_{1}+X_{2}, Y_{2}=X_{1}-X_{2}\), 求 \(\left(Y_{1}, Y_{2}\right)\) 的密度函数.

用公式 (4.11) 不难算出密度函数为 \(l\left(y_{1}, y_{2}\right)=\frac{1}{2} \mathrm{e}^{-y_{1}}\). 问题在于: 这个表达式只在一定范围 \(B\) 内有效, 在 \(B\) 外为 \(0 . B\) 是什么? 这就要考虑到 \(\left(X_{1}, X_{2}\right)\) 只在第一象限 \(A\) 内大于 \(0 . A\) 的两条边, 即两轴的正半部, 分别相应于 \(\left(Y_{1}, Y_{2}\right)\) 平面上的直线 \(Y_{1}=Y_{2}\) 和 \(Y_{1}=-Y_{2}\) (见图 2.10). 另外, \(Y_{1}=X_{1}+X_{2}\) 必大于 \(0, Y_{1}\) 必大于 \(Y_{2}\). 故 \(\left(Y_{1}, Y_{2}\right)\) 只能落在上述两条直线所夹出的包含 \(Y_{1}\) 正半轴的那部分, 即图 2.10 中标示的 \(B\).

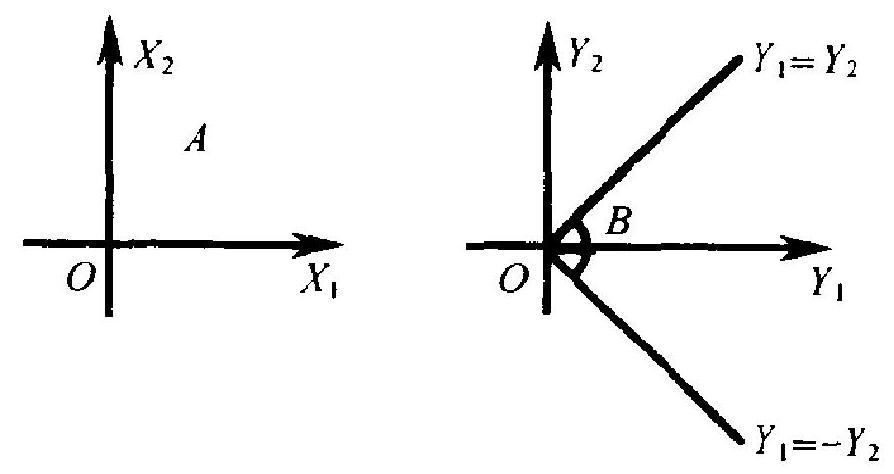
图 2.10

有时,我们所要求的只是一个函数

\[ Y_{1}=g_{1}\left(X_{1}, X_{2}\right) \]

的分布. 一个办法是对任何 \(y\) 找出 \(\left\{Y_{1} \leqslant y\right\}\) 在 \(\left(X_{1}, X_{2}\right)\) 平面上对应的区域 \(\left\{g_{1}\left(X_{1}, X_{2}\right) \leqslant y\right\}\), 记为 \(A_{y}\). 然后由 \(P\left(Y_{1} \leqslant y\right)=\) \(\iint_{A y} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2}\) 找出 \(Y_{1}\) 的分布. 另一个办法是配上另一个函数 \(Y_{2}=g_{2}\left(X_{1}, X_{2}\right)\), 使 \(\left(X_{1}, X_{2}\right)\) 到 \(\left(Y_{1}, Y_{2}\right)\) 成一一对应变换. 然后按 (4.11) 找出 \(\left(Y_{1}, Y_{2}\right)\) 的联合密度函数 \(l\left(y_{1}, y_{2}\right)\). 最后, \(Y_{1}\) 的密度函数由公式 \(\int_{-\infty}^{\infty} l\left(y_{1}, y_{2}\right) \mathrm{d} y_{2}\) 给出 (见(2.9)). 后面将给出使用这个方法的重要例子.

以上所说可完全平行地推广到 \(n\) 个变量的情形: 设 \(\left(X_{1}, \cdots\right.\), \(\left.X_{n}\right)\) 有密度函数 \(f\left(x_{1}, \cdots, x_{n}\right)\), 而

\[ Y_{i}=g_{i}\left(X_{1}, \cdots, X_{n}\right), i=1, \cdots, n \]

构成 \(\left(X_{1}, \cdots, X_{n}\right)\) 到 \(\left(Y_{1}, \cdots, Y_{n}\right)\) 的一- 对应变换, 其逆变换为

\[ X_{i}=h_{i}\left(Y_{1}, \cdots, Y_{n}\right), i=1, \cdots, n \]

此变换的贾可比行列式为

\[ J\left(y_{1}, \cdots, y_{n}\right)=\left|\begin{array}{ccc} \partial h_{1} / \partial y_{1} & \cdots & \partial h_{1} / \partial y_{n} \\ \cdots & \cdots & \cdots \\ \partial h_{n} / \partial y_{1} & \cdots & \partial h_{n} / \partial y_{n} \end{array}\right| \]

则 \(\left(Y_{1}, \cdots, Y_{n}\right)\) 的密度函数为

\[ \begin{aligned} l\left(y_{1}, \cdots, y_{n}\right)= & f\left(h_{1}\left(y_{1}, \cdots, y_{n}\right), \cdots, h_{n}\left(y_{1}, \cdots, y_{n}\right)\right) \\ & \cdot\left|J\left(y_{1}, \cdots, y_{n}\right)\right| \end{aligned} \]

\subsection{3 随机变量和的密度函数}

设 \(\left(X_{1}, X_{2}\right)\) 的联合密度函数为 \(f\left(x_{1}, x_{2}\right)\), 要求

\[ Y=X_{1}+X_{2} \]

的密度函数.

一个办法是考虑事件

\[ \{Y \leqslant y\}=\left\{X_{1}+X_{2} \leqslant y\right\} \]

它所对应的 \(\left(X_{1}, X_{2}\right)\) 坐标平面上的集合 \(B\), 就是图 2.11 中所示的直线 \(x_{1}+x_{2}=y\) 的下方那部分. 按密度函数的定义有

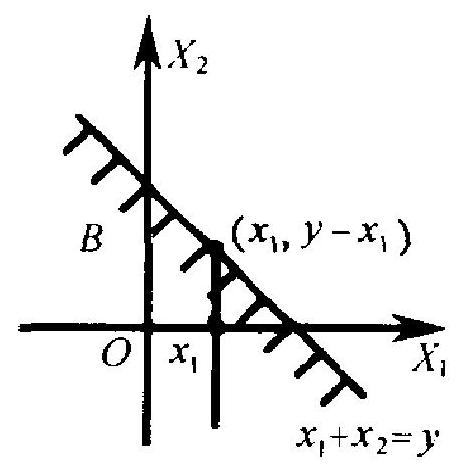
\[ \begin{aligned} P(Y & \leqslant y)=P\left(X_{1}+X_{2} \leqslant y\right) \\ & =\iint_{B} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \end{aligned} \]

图 2.11

将重积分化为黑积分, 先固定 \(x_{1}\) 对 \(x_{2}\) 积分, 积分范围为 \(-\infty\) 到 \(y-x_{1}\), 如图所示. 然后再对 \(x_{1}\) 从 \(-\infty\) 到 \(\infty\) 积分. 结果得

\[ P(Y \leqslant y)=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{y-x_{1}} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{2}\right) \mathrm{d} x_{1} \]

对 \(y\) 求导数, 即得 \(Y\) 的密度函数为

\[ l(y)=\int_{-\infty}^{\infty} f\left(x_{1}, y-x_{1}\right) \mathrm{d} x_{1} \]

\[ =\int_{-\infty}^{\infty} f(x, y-x) \mathrm{d} x \]

作变数代换 \(t=y-x\) (注意 \(y\) 是固定的), 再把积分变量 \(t\) 换回到 \(x\),也得到

\[ l(y)=\int_{-\infty}^{\infty} f(y-x, x) \mathrm{d} x \]

如果 \(X_{1}, X_{2}\) 独立, 则 \(f\left(x_{1}, x_{2}\right)=f_{1}\left(x_{1}\right) f_{2}\left(x_{2}\right)\). 这时 (4.16) 和 (4.17)有形式

\[ \begin{aligned} l(y) & =\int_{-\infty}^{\infty} f_{1}(x) f_{2}(y-x) \mathrm{d} x \\ & =\int_{-\infty}^{\infty} f_{1}(y-x) f_{2}(x) \mathrm{d} x \end{aligned} \]

这个方法在数学上一点不足的地方是要通过在积分号下求导数. 这在理论上是有条件的. 另一个做法是配上另一个函数,例如 \(Z=X_{1}\). 则

\[ Y=X_{1}+X_{2}, Z=X_{1} \]

构成 \(\left(X_{1}, X_{2}\right)\) 到 \((Y, Z)\) 的一一对应变换. 逆变换为

\[ X_{1}=Z, X_{2}=Y-Z \]

贾可比行列式为 -1 , 绝对值为 1 . 按公式 (4.11), 得 \((Y, Z)\) 的联合密度函数为 \(f(z, y-z)\). 再依公式 (2.9), 求得 \(Y\) 的密度函数 \(l(y)\) 仍为 (4.16) 式.

例 4.8 设 \(X_{1}, X_{2}\) 独立, 分别服从正态分布 \(N\left(\mu_{1}, \sigma_{1}^{2}\right)\) 和 \(N\left(\mu_{2}, \sigma_{2}^{2}\right)\). 求 \(Y=X_{1}+X_{2}\) 的密度函数.

由假定, 利用 (4.18)的第一式,有

\[ l(y)=\frac{1}{2 \pi \sigma_{1} \sigma_{2}} \int_{-\infty}^{\infty} \exp \left[-\frac{1}{2}\left(\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}}+\frac{\left(y-x-\mu_{2}\right)^{2}}{\sigma_{2}^{2}}\right)\right] \mathrm{d} x \]

经过一些初等代数的运算, 不难得到

\[ \begin{aligned} & \left(x-\mu_{1}\right)^{2} / \sigma_{1}^{2}+\left(y-x-\mu_{2}\right)^{2} / \sigma_{2}^{2} \\ & \quad=\left(\sigma_{1}^{2}+\sigma_{2}^{2}\right)^{-1}\left(y-\mu_{1}-\mu_{2}\right)^{2}+(a x-b)^{2} \end{aligned} \]

其中

\[ \begin{aligned} & a=\sigma_{1} \sigma_{2} / \sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}} \\ & b=\frac{\sigma_{1} \sigma_{2}}{\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}}}\left(\mu_{1} \sigma_{1}^{-2}+\left(y-\mu_{2}\right) \sigma_{2}^{-2}\right) \end{aligned} \]

代人(4.19), 得

\[ l(y)=\left(2 \pi \sigma_{1} \sigma_{2}\right)^{-1} \exp \left[-\frac{\left(y-\mu_{1}-\mu_{2}\right)^{2}}{2\left(\sigma_{1}^{2}+\sigma_{2}^{2}\right)}\right] \int_{-\infty}^{\infty} \mathrm{e}^{-\frac{1}{2}(a x-b)^{2}} \mathrm{~d} x \]

注意 \(a, b\) 都与 \(x\) 无关, 作变数代换 \(t=a x+b\), 并利用 \(\int_{-\infty}^{\infty} \mathrm{e}^{-t^{2} 2} \mathrm{~d} t\)

\[ \begin{aligned} =\sqrt{2 \pi}(\text { 见 }(1.15) & \text { 式), 即得 } \\ l(y)= & \left.\left(\sqrt{2 \pi\left(\sigma_{1}^{2}+\sigma_{2}^{2}\right.}\right)\right)^{-1} \times \\ & \exp \left[-\frac{1}{2}\left(y-\mu_{1}-\mu_{2}\right)^{2} /\left(\sigma_{1}^{2}+\sigma_{2}^{2}\right)\right] \end{aligned} \]

这正是正态分布 \(N\left(\mu_{1}+\mu_{2}, \sigma_{1}^{2}+\sigma_{2}^{2}\right)\) 的密度函数. 由此可见, 两个独立的正态变量的和仍服从正态分布, 且有关的参数相加.

有趣的是, 这个事实的逆命题也成立:如果 \(Y\) 服从正态分布, 而 \(Y\) 表成两个独立随机变量 \(X_{1}, X_{2}\) 之和,则 \(X_{1}, X_{2}\) 必都服从正态分布. 这个事实称为正态分布的“再生性”: 一条蚯蚂砍成两段, 仍各成一条䖵蚛, 这称为蚯蚛的再生性; 此处亦然: 一个正态变量 \(Y\) 砍成独立的两段 \(X_{1}, X_{2}\left(Y=X_{1}+X_{2}\right)\), 各段 \(X_{1}, X_{2}\) 仍不失其正态性. 这个深刻命题的证明超出了本书的范围.

不难证明: 即使 \(X_{1}, X_{2}\) 不独立,只要其联合分布为二维正态 \(N\left(\mu_{1}, \mu_{2}, \sigma_{1}^{2}, \sigma_{2}^{2}, \rho\right)\), 则 \(Y=X_{1}+X_{2}\) 仍为正态: \(Y \sim N\left(\mu_{1}+\mu_{2}\right.\), \(\left.\sigma_{1}^{2}+\sigma_{2}^{2}+2 \rho \sigma_{1} \sigma_{2}\right)\). 证明与本例相仿, 细节留给读者.

本例直接推广到 \(n\) 个变量的情形: 若 \(X_{1}, \cdots, X_{n}\) 相互独立, 分别服从正态分布 \(N\left(\mu_{1}, \sigma_{1}^{2}\right), \cdots, N\left(\mu_{n}, \sigma_{n}^{2}\right)\), 则 \(X_{1}+\cdots+X_{n}\) 服从正态分布 \(N\left(\mu_{1}+\cdots+\mu_{n}, \sigma_{1}^{2}+\cdots+\sigma_{n}^{2}\right)\).

证明很容易. 以三个变量的情形为例. 记

\[ Y=X_{1}+X_{2}+X_{3}=Z+X_{3}, Z=X_{1}+X_{2} \]

按本例结果有 \(Z \sim N\left(\mu_{1}+\mu_{2}, \sigma_{1}^{2}+\sigma_{2}^{2}\right)\). 又按定下 3.3 , 知 \(Z\) 与 \(X_{3}\) 独立. 对 \(Z\) 和 \(X_{3}\) 应用本例, 即得

\[ Y=Z+X_{3} \sim N\left(\mu_{1}+\mu_{2}+\mu_{3}, \sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}\right) \]

在介绍下面这个重要例子之前, 我们先要引进两个重要的特殊函数:

\(\Gamma\) 函数 (读作 Gamma 函数) \(\Gamma(x)\) : 通过积分

\[ \Gamma(x)=\int_{0}^{\infty} \mathrm{e}^{-t} t^{x-1} \mathrm{~d} t, x>0 \]

来定义. 此积分在 \(x>0\) 时有意义.

\(\beta\) 函数 (读作 Beta 函数) \(\beta(x, y)\) : 通过积分

\[ \beta(x, y)=\int_{0}^{1} t^{x-1}(1-t)^{y-1} \mathrm{~d} t, x>0, y>0 \]

来定义. 此积分在 \(x>0, y>0\) 时有意义.

直接算出 \(\Gamma(1)=\int_{0}^{\infty} \mathrm{e}^{-t} \mathrm{~d} t=1\), 而在作变数代换 \(t=u^{2}\) 后, 算出

\[ \begin{aligned} \Gamma(1 / 2) & =\int_{0}^{\infty} \mathrm{e}^{-t} t^{-1 / 2} \mathrm{~d} t=\int_{0}^{\infty} \mathrm{e}^{-u^{2}} u^{-1}(2 u \mathrm{~d} u) \\ & =2 \int_{0}^{\infty} \mathrm{e}^{-u^{2}} \mathrm{~d} u=\int_{-\infty}^{\infty} \mathrm{e}^{-u^{2}} \mathrm{~d} u \end{aligned} \]

令 \(u=v / \sqrt{2}\),并利用 \((1.15)\) 式,得

\[ \Gamma(1 / 2)=\frac{1}{\sqrt{2}} \int_{-\infty}^{\infty} \mathrm{e}^{-v^{2} / 2} \mathrm{~d} v=\frac{1}{\sqrt{2}} \sqrt{2 \pi}=\sqrt{\pi} \]

\(\Gamma\) 函数有重要的递推公式:

\[ \Gamma(x+1)=x \Gamma(x) \]

事实上, \(\Gamma(x+1)=\int_{0}^{\infty} e^{-t} t^{x} \mathrm{~d} t\). 作分部积分, 有

\[ \begin{aligned} \int_{0}^{\infty} \mathrm{e}^{-t} t^{x} \mathrm{~d} t & =-\int_{0}^{\infty} t^{x} \mathrm{~d}\left(\mathrm{e}^{-t}\right)=-\left.t^{x} \mathrm{e}^{-t}\right|_{0} ^{\infty}+x \int_{0}^{\infty} \mathrm{e}^{-t} t^{x-1} \mathrm{~d} t \\ & =x \Gamma(x) \end{aligned} \]

由算出的 \(\Gamma(1)\) 和 \(\Gamma(1 / 2)\), 可得出当 \(n\) 为正整数时, \(\Gamma(n)\) 和 \(\Gamma(n / 2)\) 之值 (后者当 \(n\) 为奇数时, 否则 \(n / 2\) 为整数):

\[ \Gamma(n)=(n-1) !, \Gamma(n / 2)=1 \cdot 3 \cdot 5 \cdots(n-2) 2^{-(n-1) / 2} \sqrt{\pi} \]

例如

\[ \begin{aligned} \Gamma(4) & =\Gamma(3+1)=3 \Gamma(3)=3 \cdot 2 \Gamma(2)=3 \cdot 2 \cdot 1 \Gamma(1) \\ & =3 \cdot 2 \cdot 1=3 ! \\ \Gamma(7 / 2) & =\Gamma(5 / 2+1)=(5 / 2) \Gamma(5 / 2) \\ & =(5 / 2)(3 / 2) \Gamma(3 / 2) \\ & =(5 / 2)(3 / 2)(1 / 2) \Gamma(1 / 2)=1 \cdot 3 \cdot 5 \cdot 2^{-3} \sqrt{\pi} \end{aligned} \]

\(\Gamma\) 函数与 \(\beta\) 函数之间有重要的关系式:

\[ \beta(x, y)=\Gamma(x) \Gamma(y) / \Gamma(x+y) \]

这个公式的证明见本章附录 \(A\).

由 \(\Gamma\) 函数的定义易知: 若 \(n>0\), 则函数

\[ k_{n}(x)=\left\{\begin{array}{l} \frac{1}{\Gamma\left(\frac{n}{2}\right) 2^{n / 2}} \mathrm{e}^{-x / 2} x^{(n-2) / 2}, \text { 当 } x>0 \\ 0, \quad \text { 当 } x \leqslant 0 \end{array}\right. \]

是概率密度函数. 实际上, 由 \(k_{n}(x)\) 的定义知它非负. 又 (作变数代换 \(x=2 t)\)

\[ \int_{0}^{\infty} \mathrm{e}^{-x / 2} x^{(n-2) / 2} \mathrm{~d} x=2^{n / 2} \int_{0}^{\infty} \mathrm{e}^{-t} t^{(n-2) / 2} \mathrm{~d} t=2^{n / 2} \Gamma\left(\frac{n}{2}\right) \]

故知 \(\int_{-\infty}^{\infty} k_{n}(x) \mathrm{d} x=\int_{0}^{\infty} k_{n}(x) \mathrm{d} x=1\). 因而证明了它是密度函数. 这个密度函数在统计学上很重要且很有名, 它称为 “自由度 \(n\) 的皮尔逊卡方密度” (相应的分布则称为卡方分布), 常记为 \(\chi_{n}^{2}\). \(\mathrm{K}\). 皮尔逊是英国统计学家, 现代统计学的奠基人之一. 在本书第五章中将涉及他的工作. 例 4.9 若 \(X_{1}, \cdots, X_{n}\) 相互独立, 都服从正态分布 \(N(0,1)^{*}\), 则 \(Y=X_{1}^{2}+\cdots+X_{n}^{2}\) 服从自由度 \(n\) 的卡方分布 \(\chi_{n}^{2}\).

从例 4.5 , 并注意 \(\Gamma(1 / 2)=\sqrt{\pi}\), 看出本例的结果当 \(n=1\) 时成立. 于是可用归纳法, 设此结果当 \(n\) 改为 \(n-1\) 时成立. 表 \(Y\) 为 \(Z+X_{n}^{2}\), 其中 \(Z=X_{1}^{2}+\cdots+X_{n-1}^{2}\), 则由归纳假设, 知 \(Z\) 有密度函数 \(k_{n-1}(x)\). 由例 4.5 知 \(X_{n}^{2}\) 有密度函数 \(k_{1}(x)\). 再由定理 3.3, 知 \(Z\) 与 \(X_{n}^{2}\) 独立. 于是按公式 (4.18) (用前一式), 知 \(Y\) 的密度函数为

\[ l(y)=\int_{-\infty}^{\infty} k_{n-1}(x) k_{1}(y-x) \mathrm{d} x=\int_{0}^{y} k_{n-1}(x) k_{1}(y-x) \mathrm{d} x \]

后一式是因为, \(k_{n-1}(t)\) 和 \(k_{1}(t)\) 都只在 \(t>0\) 时才不为 0 , 故有效的积分区间为 \(0 \leqslant x \leqslant y\). 以 (4.26) 中的表达式 \((n\) 分别改为 \(n-1\) 和 1) 代人上式,得

\[ \begin{aligned} l(y)= & \left(\Gamma\left(\frac{n-1}{2}\right) 2^{\frac{n-1}{2}} \Gamma\left(\frac{1}{2}\right) 2^{\frac{1}{2}}\right)^{-1} \mathrm{e}^{-y / 2} \\ & \cdot \int_{0}^{y} x^{(n-3) / 2}(y-x)^{-1 / 2} \mathrm{~d} x \end{aligned} \]

在积分中作变数代换 \(x=y t\), 得

\[ \begin{aligned} & \int_{0}^{y} x^{(n-3) / 2}(y-x)^{-1 / 2} \mathrm{~d} x \\ = & y^{(n-2) / 2} \int_{0}^{1} t^{(n-3) / 2}(1-t)^{-1 / 2} \mathrm{~d} t \\ = & y^{(n-2) / 3} \beta\left(\frac{n-1}{2}, \frac{1}{2}\right) \\ = & y^{(n-2) / 2} \Gamma\left(\frac{n-1}{2}\right) \Gamma\left(\frac{1}{2}\right) / \Gamma\left(\frac{n}{2}\right) \end{aligned} \]

以此代入 (4.27), 即得 \(l(y)=k_{n}(y)\). 从而证明了本例结果对 \(n\) 也成立, 这完成了归纳证明。

常把这说成 \(X_{1}, \cdots, X_{n}\) 独立同分布并缩记为 id. (independently identically distributed), 并说 \(X_{1}, \cdots, X_{n}\) 有公共分布 \(V(0,1)\). 注意不要混渚“公共”分布和“联合”分布. 整个这假定可简记为: \(\mathrm{X}_{1}, \cdots, \mathrm{X}_{n}\) iid, \(\sim N(0,1)\). 本例也解释了在定义卡方分布时提到的“自由度 \(n\) ”这个名词. 因为 \(Y\) 表为 \(n\) 个独立变量 \(X_{1}, \cdots, X_{n}\) 的平方和,每个变量 \(X_{i}\) 都能随意变化, 可以说它有一个自由度, 共有 \(n\) 个变量, 因此有 \(n\) 个自由度, 当然这个解释只在 \(n\) 为正整数时才有效 (注意 \(k_{n}(x)\) 的定义中并不必须限制 \(n\) 为正整数, 只要 \(n>0\) 就行). 实际上, 自由度这个名词通常也只用在 \(n\) 为整数时.

卡方分布有如下的重要性质:

设 \(X_{1}, X_{2}\) 独立, \(X_{1}-\chi_{m}^{2}, X_{2} \sim \chi_{n}^{2}\), 则 \(X_{1}+X_{2} \sim \chi_{m+n}^{2}\).

证明可以直接利用和的密度公式 (4.18) 得到. 更简便的是从卡方变量的表达式出发, 设 \(Y_{1}, \cdots, Y_{m+n}\) 独立且都有分布 \(N(0,1)\). 令 \(X_{1}=Y_{1}^{2}+\cdots+Y_{m}^{2}, X_{2}=Y_{m+1}^{2}+\cdots+Y_{m+n}^{2}\). 按本例, 有

\[ X_{1} \sim \chi_{m}^{2}, X_{2} \sim \chi_{n}^{2} \]

而

\[ X_{1}+X_{2}=Y_{1}^{2}+\cdots+Y_{m+n}^{2} \]

为 \(m+n\) 个标准正态变量的平方和. 按本例其分布为 \(\chi_{m+n}^{2}\), 明所欲证.

若 \(X_{1}, \cdots, X_{n}\) 独立, 且都服从指数分布 \((1.20)\),则

\[ X=2 \lambda\left(X_{1}+\cdots+X_{n}\right) \sim \chi_{2 n}^{2} \]

首先, 由 \(X_{i}\) 的密度函数为 \((1.20)\), 知 \(2 \lambda X_{i}\) 的密度函数为 \(\frac{1}{2} \mathrm{e}^{-x / 2}\) （当 \(x>0 . x \leqslant 0\) 时为 0 ). 但在 (4.26) 中令 \(n=2\), 可知这正好是 \(\chi^{2}\) 的密度函数, 因此 \(2 \lambda X_{i}-\chi_{2}^{2}\). 再因 \(X_{1}, \cdots, X_{n}\) 独立, 利用刚才证明的性质, 即得所要的结果.

\subsection{4 随机变量商的密度函数}

设 \(\left(X_{1}, X_{2}\right)\) 有密度函数 \(f\left(x_{1}, x_{2}\right), Y=X_{2} / X_{1}\). 要求 \(Y\) 的密度函数. 为简单计,限制 \(X_{1}\) 只取正值的情况.

事件 \(\{Y \leqslant y\}=\left\{X_{2} / X_{1} \leqslant y\right\}\) 可写为 \(\left\{X_{2} \leqslant X_{1} y\right\}\), 因为 \(X_{1}>\) 0 . 这相应于图 2.12 中所标出的区域 \(B\). 通过化重积分为累积分, 得到

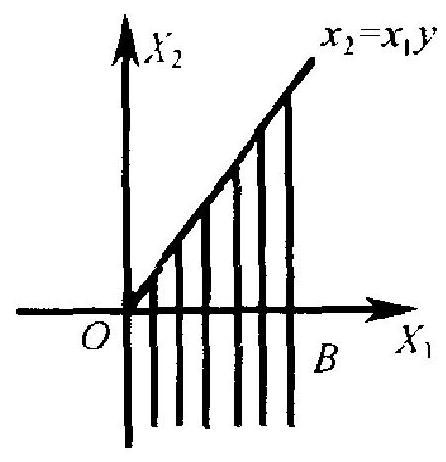
图 2.12

\[ \begin{aligned} P(Y \leqslant y) & =\iint_{B} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \\ & =\int_{0}^{\infty}\left[\int_{-\infty}^{x_{1} y} f\left(x_{1}, x_{2}\right) \mathrm{d} x_{2}\right] \mathrm{d} x_{1} \end{aligned} \]

对 \(y\) 求导, 得 \(Y\) 的密度函数为

\[ l(y)=\int_{0}^{\infty} x_{1} f\left(x_{1}, x_{1} y\right) \mathrm{d} x_{1} \]

若 \(X_{1}, X_{2}\) 独立, 则 \(f\left(x_{1}, x_{2}\right)=f_{1}\left(x_{1}\right) \cdot\) \(f_{2}\left(x_{2}\right)\), 而上式成为

\[ l(y)=\int_{0}^{\infty} x_{1} f_{1}\left(x_{1}\right) f_{2}\left(x_{1} y\right) \mathrm{d} x_{1} \]

(4.28) 式也可以通过添加一个变换 \(Z=X_{1}\), 再运用公式 (4.11) 和 (2.9)得到, 建议读者自己去完成. 这个做法不须在积分号下求导数.

下面考察两个在统计学上十分重要的例子.

例 4.10 设 \(X_{1}, X_{2}\) 独立, \(X_{1} \sim \chi_{n}^{2}\) 独立, \(X_{2} \sim N(0,1)\), 而 \(Y\) \(=X_{2} / \sqrt{X_{1} / n}\). 求 \(Y\) 的密度函数.

记 \(Z=\sqrt{X_{1} / n}\). 先要求出 \(Z\) 的密度函数 \(g(z)\). 有

\[ \begin{aligned} P(Z \leqslant z) & =P\left(\sqrt{X_{1} / n} \leqslant z\right)=P\left(X_{1} \leqslant n z^{2}\right) \\ & =\int_{0}^{n z^{2}} k_{n}(x) \mathrm{d} x \end{aligned} \]

两边对 \(Z\) 求导, 得 \(Z\) 的密度函数为

\[ g(z)=2 n z k_{n}\left(n z^{2}\right) \]

其次, 以 \(f_{1}\left(x_{1}\right)=2 n x_{1} k_{n}\left(n x_{1}^{2}\right)\) 和 \(f_{2}\left(x_{2}\right)=\sqrt{2 \pi}^{-1} \mathrm{e}^{-x_{2}^{2} / 2}\) 应用公式 (4.29), 得 \(Y\) 的密度函数, 记之为 \(t_{n}(y)\), 等于

\[ t_{n}(y)=\sqrt{2 \pi}^{-1}\left(2^{n / 2} \Gamma(n / 2)\right)^{-1} \int_{0}^{\infty} 2 n x_{1}^{2} \mathrm{e}^{-n x_{1}^{2} / 2}\left(n x_{1}^{2}\right)^{(n-2) / 2} \]

\[ \begin{aligned} & \cdot \mathrm{e}^{-\left(x_{1} y\right)^{2} / 2} \mathrm{~d} x_{1} \\ = & \sqrt{2 \pi}{ }^{-1}\left(2^{n / 2} \Gamma(n / 2)\right)^{-1} 2 n^{n / 2} \\ & \cdot \int_{0}^{\infty} x_{1}^{n} \exp \left[-\frac{1}{2}\left(n x_{1}^{2}+x_{1}^{2} y^{2}\right)\right] \mathrm{d} x_{1} \end{aligned} \]

作变数代换 \(x_{1}=\sqrt{2 /\left(n+y^{2}\right)} \sqrt{t}\), 上面的积分变为

\[ \begin{aligned} & \frac{1}{2}\left(\frac{2}{n+y^{2}}\right)^{(n+1) / 2} \int_{0}^{\infty} \mathrm{e}^{-t} t^{(n-1) / 2} \mathrm{~d} t \\ = & \frac{1}{2}\left(\frac{2}{n+y^{2}}\right)^{(n+1) / 2} \Gamma\left(\frac{n+1}{2}\right) \end{aligned} \]

以此代人 (4.30), 并略加整理, 即得 \(Y=X_{2} / \sqrt{X_{1} / n}\) 的密度函数为

\[ t_{n}(y)=\frac{\Gamma((n+1) / 2)}{\sqrt{n \pi} \Gamma(n / 2)}\left(1+\frac{y^{2}}{n}\right)^{-\frac{n+1}{2}} \]

这个密度函数称为 “自由度 \(n\) 的 \(t\) 分布” 的密度函数,常简记为 \(Y \sim t_{n}\). 这个分布是英国统计学家 W. 哥色特在 1908 年以“student”的笔名首次发表的. 它是数理统计学中最重要的分布之一, 今后我们将见到这个分布在统计学上的许多应用.

这个密度函数关于原点对称, 其图形与正态 \(N(0,1)\) 的密度函数的图形相似, 以后我们将见到 (见第三章 3.4 节), 当自由度 \(n\) 很大时, \(t\) 分布确实接近于标准正态分布.

例 4.11 设 \(X_{1}, X_{2}\) 独立, \(X_{1} \sim \chi_{n}^{2}, X_{2} \sim \chi_{m}^{2}\), 而 \(Y=m^{-1}\) \(X_{2} / n^{-1} X_{1}\). 求 \(Y\) 的密度函数.

因为 \(X_{1}, X_{2}\) 独立,故 \(n^{-1} X_{1}\) 和 \(m^{-1} X_{2}\) 也独立. 由 \(X_{1} \sim \chi_{n}^{2}\) 和 \(X_{2} \sim \chi_{m}^{2}\) 易求出 \(n^{-1} X_{1}\) 和 \(m^{-1} X_{2}\) 的密度函数分别为 \(n k_{n}\) \(\left(n x_{1}\right)\) 和 \(m k_{m}\left(m x_{2}\right)\). 以此代人 (4.29), 得 \(Y\) 的密度函数,记之为 \(f_{m n}(y)\) (注意 \(m\) 在前, \(m\) 是分子 \(X_{2}\) 的自由度), 等于

\[ \begin{aligned} f_{m n}(y) & =m n \int_{0}^{\infty} x_{1} k_{n}\left(n x_{1}\right) k_{m}\left(m x_{1} y\right) \mathrm{d} x_{1} \\ & =m n\left[2^{m / 2} \Gamma\left(\frac{m}{2}\right) 2^{n / 2} \Gamma\left(\frac{n}{2}\right)\right]^{-1} \end{aligned} \]

\[ \begin{aligned} & \int_{0}^{\infty} x_{1} \mathrm{e}^{-n x_{1} / 2}\left(n x_{1}\right)^{n / 2-1} \mathrm{e}^{-m x_{1} y / 2}\left(m x_{1} y\right)^{m / 2-1} \mathrm{~d} x_{1} \\ = & {\left[2^{(m+n) / 2} \Gamma\left(\frac{m}{2}\right) \Gamma\left(\frac{n}{2}\right)\right]^{-1} m^{m / 2} n^{n / 2} y^{m / 2-1} } \\ & \cdot \int_{0}^{\infty} \mathrm{e}^{(m y+n) x_{1} / 2} x_{1}^{(m+n) / 2-1} \mathrm{~d} x_{1} \end{aligned} \]

作变数代换 \(t=(m y+n) x_{1} / 2\),上式的积分化为

\[ \begin{aligned} & 2^{(m+n) / 2}(m y+n)^{-(m+n) / 2} \int_{0}^{\infty} \mathrm{e}^{-t} t^{(m+n) / 2-1} \mathrm{~d} t \\ = & 2^{(m+n) / 2}(m y+n)^{-(m+n) / 2} \Gamma\left(\frac{m+n}{2}\right) \end{aligned} \]

以此代人上式,得

\[ \begin{aligned} & f_{m n}(y)=m^{m / 2} n^{n / 2} \frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right) \Gamma\left(\frac{n}{2}\right)} y^{m / 2-1}(m y+n)^{-(m+n) / 2}, \\ & y>0 \end{aligned} \]

当 \(y \leqslant 0\) 时 \(f_{m n}(y)=0\), 因为 \(Y\) 只取正值.

这个分布称为“自由度 \(m, n\) 的 \(F\) 分布” (注意分子的自由度在前). 它也是数理统计学上的一个重要分布, 有很多应用, 常记为 \(F_{m n}: Y \sim F_{m n}\).

人们有时把 \(\chi^{2}, t\) 和 \(F\) 这三个分布合称为 “统计上的三大分布”, 就是因为它们在统计学中有广泛的应用. 这些应用的相当大一部分根由, 在于以下的几条重要性质. 它们的证明可参见本章附录 \(B\).

\(1^{\circ}\) 设 \(X_{1}, \cdots, X_{n}\) 独立同分布, 有公共的正态分在 \(N\left(\mu, \sigma^{2}\right)\). 记 \(\bar{X}=\left(X_{1}+\cdots+X_{n}\right) / n, S^{2}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} /(n-\) 1). 则

\[ (n-1) S^{2} / \sigma^{2}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} / \sigma^{2} \sim \chi_{n-1}^{2} \]

\(2^{\circ}\) 设 \(X_{1}, \cdots, X_{n}\) 的假定同 \(1^{\circ}\), 则

\[ \sqrt{n}(\bar{X}-\mu) / S-t_{n-1} \]

\(3^{\circ}\) 设 \(X_{1}, \cdots, X_{n}, Y_{1}, \cdots, Y_{m}\) 独立, \(X_{i}\) 各有分布 \(N\left(\mu_{1}, \sigma_{1}^{2}\right)\), \(Y_{j}\) 各有分布 \(N\left(\mu_{2}, \sigma_{2}^{2}\right)\), 则

\[ \text { a. } \begin{aligned} & {\left[\sum_{j=1}^{m}\left(Y_{j}-\bar{Y}\right)^{2} /\left(\sigma_{2}^{2}(m-1)\right)\right] /\left[\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} /\left(\sigma_{1}^{2}(n-1)\right)\right] } \\ & \sim F_{m-1, n-1} \end{aligned} \]

b. 若 \(\sigma_{1}^{2}=\sigma_{2}^{2}\), 则

\[ \begin{aligned} & \sqrt{\frac{n m(n+m-2)}{n+m}}\left[(\bar{X}-\bar{Y})-\left(\mu_{1}-\mu_{2}\right)\right] \\ & /\left[\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}+\sum_{j=1}^{m}\left(Y_{j}-\bar{Y}\right)^{2}\right]^{1 / 2} \sim t_{n+m-2} \end{aligned} \]

2.4 随机变量的函数的概率分布⚓︎

评论