3.4 大数定理

3.4 大数定理和中心极限定理

在数学中大家都注意到过这样的现象: 有的时候一个有限的 和很难求, 但一经取极限由有限过渡到无限, 则问题反而好办. 例 如, 若要对某一有限范围的 \(x\) 计算和

\[ a_{n}(x)=1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\cdots+\frac{x^{n}}{n !} \]

则在 \(n\) 固定但很大时, 很难求. 而一经取极限, 则有简单的结果:

• 140 • \(\lim _{n \rightarrow \infty} a_{n}(x)=\mathrm{e}^{x}\). 利用这个结果, 当 \(n\) 很大时, 可以把 \(\mathrm{e}^{x}\) 作为 \(a_{n}(x)\) 的近似值.

在概率论中也存在着这种情况. 如果 \(X_{1}, X_{2}, \cdots, X_{n}\) 是一些 随机变量, 则 \(X_{1}+\cdots+X_{n}\) 的分布,除了若干例外,算起来很复杂. 因而自然地会提出问题: 可否利用极限的方法来进行近似计算? 事实证明这不仅可能, 且更有利的是: 在很一般的情况下, 和的极 限分布就是正态分布. 这一事实增加了正态分布的重要性. 在概率 论上, 习惯于把和的分布收敛于正态分布的那一类定理都叫做 “中 心极限定理”. 在本节 3.4.2 段中我们将列述这类定理中最简单, 然而也是最重要的一种情况.

在概率论中,另一类重要的极限定理是所谓“大数定理”. 它是 由概率的统计定义“频率收敛于概率”引伸而来.为描述这一点,我 们把频率通过一些随机变量的和表示出来.设做了 \(n\) 次独立试 验, 每次观察某事件 \(A\) 是否发生. 按 (1.20) 式定义随机变量 \(X_{i}, i\) \(=1, \cdots, n\). 则在这 \(n\) 次试验中事件 \(A\) 一共出现了 \(X_{1}+\cdots+X_{n}\) 次, 而频率为

\[ p_{n}=\left(X_{1}+\cdots+X_{n}\right) / n=\bar{X}_{n} \]

若 \(P(A)=p\), 则 “频率趋于概率” 就是说, 在某种意义下 (详见下 文), 当 \(n\) 很大时 \(p_{n}\) 接近 \(p\). 但 \(p\) 就是 \(X_{i}\) 期望值, 故也可以写成:

当 \(n\) 很大时 \(\bar{X}_{n}\) 接近于 \(X_{i}\) 的期望值.

按这个表述, 问题就可以不必局限于 \(X_{i}\) 只取 0,1 两个值的情 形. 事实也是如此. 这就是较一般情况下的大数定理. “大数” 的意 思, 就是指涉及大量数目的观察值 \(X_{i}\), 它表明这种定理中指出的 现象, 只有在大量次数的试验和观察之下才能成立.例如,一所大 学可能包含上万名学生, 每人有其身高. 如果我们随意观察一个学 生的身高 \(X_{1}\), 则 \(X_{1}\) 与全校学生的平均身高 \(a\) 可能相去甚远. 如 果我们观察 10 个学生的身高而取其平均,则它有更大的机会与 \(a\) 更接近些. 如观察 100 个, 则其平均又能更与 \(a\) 接近些. 这些都是 我们日常经验中所体验到的事实. 大数定理对这一点从理论的高 度给予概括和论证。

0.1. 1 大数定理

定理 4.1 设 \(X_{1}, X_{2}, \cdots, X_{n}, \cdots\) 是独立同分布的随机变量， 记它们的公共均值为 \(a\). 又设它们的方差存在并记为 \(\sigma^{2}\). 则对任 意给定的 \(\varepsilon>0\) 有

\[ \lim _{n \rightarrow \infty} P\left(\left|\bar{X}_{n}-a\right| \geqslant \varepsilon\right)=0 \quad\left(\bar{X}_{n} \text { 见(4.1) }\right) \]

(4.2) 这个式子指出了 “当 \(n\) 很大时, \(\bar{X}_{n}\) 接近 \(a\) ” 的确切含 义: 它的意义是概率上的, 不同于微积分意义下某一列数 \(a_{n}\) 收敛 于数 \(a\). 按 (4.2) 只是说: 不论你给定怎样小的 \(\varepsilon>0, \bar{X}_{n}\) 与 \(a\) 的偏 离有否可能达到 \(\varepsilon\) 或更大呢? 这是可能的, 但当 \(n\) 很大时, 出现这 种较大偏差的可能性很小, 以致当 \(n\) 很大时, 我们有很大的 (然而 不是百分之百的)把握断言 \(\bar{X}_{n}\) 很接近 \(a\). 拿上面学生身高的那个 例子说, 即使你抽了 100 个以至 1000 个学生, 你有没有绝对的把 握说, 这 100 个或 1000 个学生的平均身高一定很接近全校学生的 平均身高 \(a\) 呢? 没有,因为理论上不能排除这种可能性: 你碰巧 把全校中那 100 或 1000 个最高的学生都抽出来了. 这时你计算的 \(\bar{X}_{n}\) 就会与 \(a\) 有很大差距. 但我们也能相信, 如果抽样真是随机的 (每一学生有同等被抽出的机会), 则随着抽样次数增多, 这样的可 能性会愈来愈小. 这就是 (4.2) 式的意思. 像 (4.2) 式这样的收敛 性, 在概率论中叫做“ \(\bar{X}_{n}\) 依概率收敛于 \(a\) ”。

为了证明定理 4.1 , 需要下面的概率不等式:

马尔科夫不等式 若 \(Y\) 为只取非负值的随机变量, 则对任给 常数 \(\varepsilon>0\) 有

\[ P(Y \geqslant \varepsilon) \leqslant E(Y) / \varepsilon \]

设 \(Y\) 为连续型变量, 密度函数为 \(f(y)\). 因为 \(Y\) 只取非负值, 有 \(f(y)=0\) 当 \(y<0\). 故

\[ E(Y)=\int_{0}^{\infty} y f(y) \mathrm{d} y \geqslant \int_{\varepsilon}^{\infty} y f(y) \mathrm{d} y \]

因为在 \([\varepsilon, \infty)\) 内总有 \(y \geqslant \varepsilon\), 且 \(\int_{\varepsilon}^{\infty} f(y) \mathrm{d} y\) 就是 \(P(Y \geqslant \varepsilon)\). 故

\[ E(Y) \geqslant \int_{\varepsilon}^{\infty} y f(y) \mathrm{d} y \geqslant \varepsilon \int_{\varepsilon}^{\infty} f(y) \mathrm{d} y=\varepsilon P(Y \geqslant \varepsilon) \]

即 (4.3)，当 \(Y\) 为离散型时证明相似,请读者自己完成.

不等式 (4.3) 的一个重要特例为

契比雪夫不等式. 若 \(\operatorname{Var}(Y)\) 存在, 则

\[ P(|Y-E Y| \geqslant \varepsilon) \leqslant \operatorname{Var}(Y) / \varepsilon^{2} \]

为证此, 只须在 (4.3) 式中以 \([Y-E Y]^{2}\) 代 \(Y, \varepsilon^{2}\) 代 \(\varepsilon\), 并注意 \(P\left((Y-E Y)^{2} \geqslant \varepsilon^{2}\right)=P(|Y-E Y| \geqslant \varepsilon)\) 即可.

现在转到定理 4.1 的证明. 利用契比雪夫不等式 (4.4), 并注 意 \(E\left(\bar{X}_{n}\right)=\sum_{i=1}^{n} E\left(X_{i}\right) / n=n a / n=a\), 得

\[ P\left(\left|\bar{X}_{n}-a\right| \geqslant \varepsilon\right) \leqslant \operatorname{Var}\left(\bar{X}_{n}\right) / \varepsilon^{2} \]

因为 \(\bar{X}_{n}=\frac{1}{n}\left(X_{1}+\cdots+X_{n}\right)\) 而 \(X_{1}, \cdots, X_{n}\) 独立, 有

\[ \operatorname{Var}\left(\bar{X}_{n}\right)=\frac{1}{n^{2}} \sum_{i=1}^{n} \operatorname{Var}\left(X_{i}\right)=\frac{1}{n^{2}} n \sigma^{2}=\sigma^{2} / n \]

以此代入 \((4.5)\), 得

\[ P\left(\left|\bar{X}_{n}-a\right| \geqslant \varepsilon\right) \leqslant \sigma^{2} /\left(n \varepsilon^{2}\right) \rightarrow 0 \text {, 当 } n \rightarrow \infty \]

这证明了(4.2).

定理 4.1 的一个重要特例, 即前面提到的“频率收玫于概率”:

\[ \lim _{n \rightarrow \infty} P\left(\left|p_{n}-p\right| \geqslant \varepsilon\right)=0 \]

这个定理是最早的一个大数定理, 是伯努利在 1713 年一本著作中 证明的, 常称为伯努利大数定理.

大数定理的研究是概率论中一个很重要、古老且至今仍尚活 跃的课题, 有许多深刻的结果. 例如, 不用假定 \(X_{i}\) 的方差存在也 可以证明 (4.2) 式: \(X_{1}, X_{2}, \cdots\) 不必同分布甚至也可以不独立 (当然 仍得有一定限制), 收玫也可以改成其他更强的形式等. 这些都超 出本书的范围之外. 在概率论中, 大数定理常称为 “大数定律”. 这个字面上的不 同, 也不见得有很特殊的含义. 但是, “定理”一词往往用于指那种 能用数学工具严格证明的东西, 而 “定律” 则不一定是这样. 如牛顿 的力学三大定律, 电学中的欧姆定律之类. 这夷涉到一个从哪个角 度去看的问题. 像 (4.2) 式这样有确切数学表述, 并能在一定的理 论框架内证明的结果, 称之为 “定理” 无疑是恰当的. 可是, 当我们 泛泛地谈论“平均值的稳定性” (即稳定到理论上的期望值) 时, 这 表述了一种全人类多年的集体经验, 有些哲理的味道. 且这种意识 也远早于现代概率论给之以严格表述之前, 因此, 称之为“定律”也 不算不恰当.

0.2. 2 中心极限定理

中心极限定理的意义已在本节开始处阐述过了. 如我们所曾 指出的, 这是指一类定理. 下面的定理 4.2 是其中之一:

定理 4.2 设 \(X_{1}, X_{2}, \cdots, X_{n}, \cdots\) 为独立同分布的随机变量, \(E\left(X_{i}\right)=a, \operatorname{Var}\left(X_{i}\right)=\sigma^{2}, 0<\sigma^{2}<\infty\). 则对任何实数 \(x\), 有

\[ \lim _{n \rightarrow \infty} P\left(\frac{1}{\sqrt{n} \sigma}\left(X_{1}+\cdots+X_{n}-n a\right) \leqslant x\right)=\Phi(x) \]

这里 \(\Phi(x)\) 是标准正态分布 \(N(0,1)\) 的分布函数, 即

\[ \Phi(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \mathrm{e}^{-t^{2} / 2} \mathrm{~d} t \]

注意 \(X_{1}+\cdots+X_{n}\) 有均值 \(n a\), 方差 \(n \sigma^{2}\). 故

\[ \left(X_{1}+\cdots+X_{n}-n a\right) /(\sqrt{n} \sigma) \text {. } \]

就是 \(X_{1}+\cdots+X_{n}\) 的标准化,即使其均值变为 0 方差变为 1 , 以与 \(N(0,1)\) 的均值方差符合.

(4.7)告诉我们, 虽则在一般情况下我们很难求出 \(X_{1}+\cdots+\) \(X_{n}\) 的分布的确切形式, 但当 \(n\) 很大时, 可以通过 \(\Phi(x)\) 给出其近 似值. 例如, 若已知 \(a=1, \sigma^{2}=4, n=100\). 要求 \(P\left(X_{1}+\cdots+X_{100}\right.\) \(\leqslant 125)\). 因 \(n a=100, \sqrt{n} \sigma=20\), 把事件 \(X_{1}+\cdots+X_{100} \leqslant 125\) 改写 为 \(\left(X_{1}+\cdots+X_{100}-100\right) / 20 \leqslant 1.25\), 用 (4.7) 得到上述概率的近 似值为 \(\Phi(1.25)=0.8944\). 这里当然有一定的误差. 有许多研究 工作就是为了估计这种误差, 也得出了一些深刻的结果. 但是, 这 种误差估计要求对 \(X_{i}\) 的分布或其矩有一定的了解.

定理 4.2 通称为林德伯格定理或林德伯格一莱维定理, 是这两 位学者在本世纪 20 年代证明的. “中心极限定理”的命名也是始于 这个时期, 它是波伊亚在 1920 年给出的. 但定理 4.2 并非最早的 中心极限定理. 历史上最早的中心极限定理是定理 4.2 的一个特 例, 即当 \(X_{i}\) 由 (1.20) 式定义时, 这时, 如以前多次指出的, \(X_{1}+\cdots\) \(+X_{n}\) 就是某事件 \(A\) 在 \(n\) 次独立试验中发生的次数. 这个特例很 重要, 值得单独列为一条定理.

定理 4.3 设 \(X_{1}, X_{2}, \cdots, X_{n}, \cdots\) 独立同分布, \(X_{i}\) 分布是

\[ P\left(X_{i}=1\right)=p, P\left(X_{i}=0\right)=1-p, 0<p<1 \]

则对任何实数 \(x\), 有

\[ \lim _{n \rightarrow \infty} P\left(\frac{1}{\sqrt{n p(1-p)}}\left(X_{1}+\cdots+X_{n}-n p\right) \leqslant x\right)=\Phi(x) \]

定理 4.3 是定理 4.2 的特例, 只须注意 \(E\left(X_{i}\right)=p, \operatorname{Var}\left(X_{i}\right)\) \(=p(1-p)\). 又此处 \(X_{1}+\cdots+X_{n}\) 服从二项分布 \(B(n, p)\), 故定理 4.3 是用正态分布去逼近二项分布. 在第二章例 1.2 曾指出过用 波哇松分布逼近二项分布.二者的应用不同: (4.9) 用于 \(p\) 固定， 因而当 \(n\) 很大时 \(n p\) 很大. 而波哇松逼近则用于 \(p\) 很小(可设想成 \(p\) 随 \(n\) 变化以趋向于 0 ) 但 \(n p=\lambda\) 不太大时. 共同之点是 \(n\) 必须 相当大.

定理 4.3 称为棣莫弗一拉普拉斯定理,是历史上最早的中心极 限定理. 1716 年棣莫弗讨论了 \(p=\frac{1}{2}\) 的情形,而拉普拉斯则把它 推广到一般 \(p\) 的情形.

如果 \(t_{1}, t_{2}\) 是两个正整数, \(t_{1}<t_{2}\). 则当 \(n\) 相当大时,按 (4.9) 近似地有

\[ P\left(t_{1} \leqslant X_{1}+\cdots+X_{n} \leqslant t_{2}\right) \approx \Phi\left(y_{2}\right)-\Phi\left(y_{1}\right) \]

其中

\[ y_{i}=\left(t_{i}-n p\right) / \sqrt{n p(1-p)}, \quad i=1,2 \]

我们指出:若把 \(y_{1}, y_{2}\) 修正为

\[ \begin{aligned} & y_{1}=\left(t_{1}-\frac{1}{2}-n p\right) / \sqrt{n p(1-p)} \\ & y_{2}=\left(t_{2}+\frac{1}{2}-n p\right) / \sqrt{n p(1-p)} \end{aligned} \]

再应用公式 (4.10), 则一般可提高

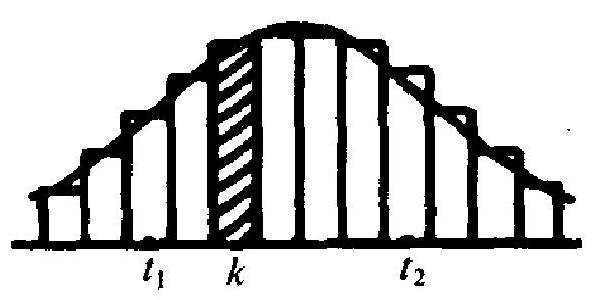
图 3.7 精度. 其道理可以从图 3.7 看出. 此图中每一矩形小条底边长为 1 , 底边中点为非负整数 \(k\), 而矩形的 高, 就是 \(P\left(X_{1}+\cdots+X_{n}=k\right)\), 即 二项概率 \(b(k ; n, p)\). 图中的曲线 则是正态分布 \(N(n p, n p(1-p))\) 的密度函数的曲线. 近似式 (4.10) 的意思, 无非是用这曲线下的面 积来近似代替这些矩形条的面积. 可是细看图形 3.7, 可知,包括 点 \(t_{1}, t_{1}+1, \cdots, t_{2}\), 这些小条在横轴上所占范围, 是左起 \(t_{1}-1 / 2\), 右止 \(t_{2}+1 / 2\), 故曲线下的面积, 也应在这两个起止点之间去计 算. 这就是修正公式 (4.12)的来由. 当 \(n\) 很大时, 这个修正并不很 重要,但在 \(n\) 不太大时则有比较大的影响.

例 4.1 设某地区内原有一家小型电影院, 因不敷需要, 拟筹 建一所较大型的. 设据分析, 该地区每日平均看电影者约有 \(n=\) 1600 人, 且预计新电影院建成开业后, 平均约有 \(3 / 4\) 的观众将去 这新影院.

现该影院在计划其座位数时,要求座位数尽可能多,但“空座 达到 200 或更多”的概率又不能超过 0.1. 问设多少座位为好?

设把每日看电影的人排号为 \(1,2 \cdots, 1600\), 且令

\[ X_{i}=\left\{\begin{array}{l} 1, \text { 若第 } i \text { 个观众去新影院 } \\ 0, \text { 若不然 } \end{array} \quad i=1, \cdots, 1600\right. \]

则按假定有 \(P\left(X_{i}=1\right)=3 / 4, P\left(X_{i}=0\right)=1 / 4\). 又假定各观众去不 去电影院系独立选择, 则 \(X_{1}, X_{2}, \cdots\) 是独立随机变量.

现设座位数为 \(m\), 则按要求

\[ P\left(X_{1}+\cdots+X_{1600} \leqslant m-200\right) \leqslant 0.1 \]

在这个条件下取 \(m\) 最大. 这显然就是在上式取等号时, 因为 \(n p=\) \(1600 \cdot(3 / 4)=1200, \sqrt{n p(1-p)}=10 \sqrt{3}\), 按 (4.12) 的修正, \(m\) 应 满足条件

\[ \Phi\left(\left(m-200+\frac{1}{2}-1200\right) /(10 \sqrt{3})\right)=0.1 \]

查 \(\Phi(x)\) 的表得知, 当 \(\Phi(x)=0.1\) 时, \(x=-1.2816^{*}\). 由

\[ (m-200+1 / 2-1200) /(10 \sqrt{3})=-1.2816 \]

定出 \(m=1377.31 \approx 1377\). 在本例中, \((4.12)\) 式的修正没有什么影 响.

直到本世纪 30 年代, 中心极限定理的研究曾是概率论的一个 重要内容, 至今仍是一个活跃的方向. 推广的方向如独立不同分布 以至非独立的情形, 由中心极限定理而引起的误差的估计, 以及与 之相关联的问题如大偏差问题之类.

评论

登录github的账号后，可以直接在下方评论框中输入。

如果想进行更详细的讨论(如排版、上传图片等)，选择一个反应后并点击上方的文字，进入论坛页面。