4.2 矩估计、极大似然估计和贝叶斯估计

4.2 矩估计、极大似然估计和贝叶斯估计

0.1. 1 参数的点估计问题

设有一个统计总体, 以 \(f\left(x, \theta_{1}, \cdots, \theta_{k}\right)\) 记其概率密度函数 (若 总体分布为连续型的), 或其概率函数 (若总体分布为离散型的), 以后, 为避免每次重复交代这两种情况, 我们约定称 \(f\left(x, \theta_{1}, \cdots\right.\), \(\left.\theta_{k}\right)\) 为“总体分布”, 其具体含义视其为连续型或离散型而定. 这分 布包含 \(k\) 个末知参数 \(\theta_{1}, \cdots, \theta_{k}\). 例如对正态总体 \(N\left(\mu, \sigma^{2}\right)\), 有 \(\theta_{1}\) \(=\mu, \theta_{2}=\sigma^{2}\), 而

• 158 •

\[ f\left(x, \theta_{1}, \theta_{2}\right)=\left(\sqrt{2 \pi \theta_{2}}\right)^{-1} \exp \left(-\frac{1}{2 \theta_{2}}\left(x-\theta_{1}\right)^{2}\right),-\infty<x<\infty \]

苃总体有二项分布 \(B(n, p)\), 则 \(\theta_{1}=p\), 而

\[ f\left(x, \theta_{1}\right)=\left(\begin{array}{l} n \\ x \end{array}\right) \theta_{1}^{x}\left(1-\theta_{1}\right)^{n-x}, x=0,1, \cdots, n \]

当 \(k=1\), 即只有一个参数时, 就用 \(\theta\) 代替 \(\theta_{1}\).

参数估计问题的一般提法是: 设有了从总体中抽出的样本 \(X_{1}, \cdots, X_{n}\) (在 4.1 节 4.1 .3 段中已说明过, 当不作特殊申明时, 样 本就是指独立随机样本, 即 \(X_{1}, \cdots, X_{n}\) 独立同分布, 其公共分布就 是总体分布), 要依据这些样本去对参数 \(\theta_{1}, \cdots, \theta_{k}\) 的末知值作出 估计. 当然,我们也可以只要求什计 \(\theta_{1}, \cdots, \theta_{k}\) 中的一部分,或估计 它们的某个已知函数 \(g\left(\theta_{1}, \cdots, \theta_{k}\right)\). 例如, 为要估计 \(\theta_{1}\), 我们需要 构造出适当的统计量 \(\hat{\theta}_{1}=\hat{\theta}_{1}\left(X_{1}, \cdots, X_{n}\right)\). 每当有了样本 \(X_{1}, \cdots\), \(X_{n}\), 就代人函数 \(\hat{\theta}_{1}\left(X_{1}, \cdots, X_{n}\right)\) 算出一个值, 用来作为 \(\theta_{1}\) 的估计 值. 为着这样的特定目的而构造的统计量 \(\hat{\theta}_{1}\), 叫做 ( \(\theta_{1}\) 的) 估计量. 由于末知参数 \(\theta_{1}\) 是数轴上的一个点,用 \(\hat{\theta}_{1}\) 去估计 \(\theta_{1}\), 等于用一个 点去估计另一个点, 所以这样的估计叫做点估计, 以别于将在 4.4 节讨论的区间估计。

在本节中我们要讨论几种常用的点估计方法, 这些方法大多 是基于某种直观上的考虑. 同一个参数往往可以用若干个看来都 合理的方法去估计. 因此有一个判断优劣的问题, 这就要为估计量 的优劣制定准则, 进而研究在某种准则下寻找最优估计量的问题. 这就是参数估计这个数理统计学分支的重要内容. 这些概念将在 以后作更具体的解释.

0.2. 2 矩估计法

矩估计法是 \(\mathrm{K}\). 皮尔逊在上世纪末到本世纪初的一系列文章 中引进的. 这个方法的思想很简单: 设总体分布为 \(f\left(x, \theta_{1}, \cdots\right.\), \(\theta_{k}\) ), 则它的矩 (原点矩和中心矩都可以, 此处以原点矩为例)

\[ \begin{gathered} \alpha_{m}=\int_{-\infty}^{\infty} x^{m} f\left(x, \theta_{1}, \cdots, \theta_{k}\right) \mathrm{d} x \\ \left(\text { 或 } \sum_{i} x_{i}^{m} f\left(x_{i}, \theta_{i}, \cdots, \theta_{k}\right)\right) \end{gathered} \]

依赖于 \(\theta_{1}, \cdots, \theta_{k}\). 另一方面, 至少在样本大小 \(n\) 较大时, \(\alpha_{m}\) 又应 接近于样本原点矩 \(\alpha_{m}\). 于是

\[ \alpha_{m}=\alpha_{m}\left(\theta_{1}, \cdots, \theta_{k}\right) \approx a_{m}=\sum_{i=1}^{n} X_{i}^{m} / n \]

取 \(m=1, \cdots, k\), 并让上面的近似式改成等式, 就得到一个方程组 :

\[ \alpha_{m}\left(\theta_{1}, \cdots, \theta_{k}\right)=\alpha_{m}, m=1, \cdots, k \]

解此方程组, 得其根 \(\hat{\theta}_{i}=\hat{\theta}_{i}\left(X_{1}, \cdots, X_{n}\right), i=1, \cdots, k\). 就以 \(\hat{\theta}_{i}\) 作为 \(\theta_{i}\) 的估计. \(i=1, \cdots, k\). 如果要估计的是 \(\theta_{1}, \cdots, \theta_{k}\) 的某函数 \(g\left(\theta_{1}\right.\), \(\left.\cdots, \theta_{k}\right)\), 则用 \(\hat{g}=\hat{g}\left(X_{1}, \cdots, X_{n}\right)=g\left(\hat{\theta}_{1}, \cdots, \hat{\theta}_{k}\right)\) 去估计它. 这样定 出的估计量就叫做矩估计.

我们来举几个例子说明这个方法.

例 2.1 设 \(X_{1}, \cdots, X_{n}\) 是从正态总体 \(N\left(\mu, \sigma^{2}\right)\) 中抽出的样 本, 要估计 \(\mu\) 和 \(\sigma^{2} . \mu\) 是总体的一阶原点矩, 按矩估计, 用样本一 阶原点矩即样本均值 \(\bar{X}\) 去估计之. \(\sigma^{2}\) 是总体方差, 即总体二阶中 心矩, 可用样本二阶中心矩 \(m_{2}\) 去估计.一般,在估计方差时常用 样本方差 \(s^{2}\) 而不用 \(m_{2}\), 即对矩估计作了一定的修正. 这种修正的 理由将在下节中指出。

如果要估计的是标准差 \(\sigma\), 则由 \(\sigma=\sqrt{\sigma^{2}}\), 按矩估计法, 它可 以用 \(\sqrt{m_{2}}\) 去估计,一般用 \(\sqrt{s^{2}}=s\) 去估计, 或者还作点修正（见下 节). 又当 \(\mu \neq 0\) 时 (特别在 \(\mu>0\) 时, 在有些问题中 \(\mu\) 虽末知, 但事 先可知 \(\mu>0\). 如例 \(1.2, \mu\) 是该校大学生的平均成绩, 它必须大于 \(0), \sigma / \mu\) 称为总体的变异系数一一变异系数是以均值为单位去衡 量的总体的标准差. 在有些问题中, 反映变异程度的标准差意义如 何, 要看总体均值 \(\mu\) 而定. 比如一大群人收入的标准差为 50 元. 若其平均工资只有 70 元, 则这个变异程度可算很大了. 但若平均 1. 资为 850 元, 则这变异程度不算大. 所以, 变异系数 \(\sigma / \mu\) 不过是 一定意义下的“相对误差”. 按矩法, 为估计 \(\sigma / \mu\), 可用 \(\sqrt{m_{2}} / \bar{X}\), 一 般用 \(s / \bar{X}\).

例 2.2 设 \(X_{1}, \cdots, X_{n}\) 是从指数分布总体中抽出的样本, 要 估计参数 \(\lambda\) 的倒数 \(1 / \lambda\). 前已指出: \(1 / \lambda\) 就是总体分布的均值, 故 按矩法, 就用 \(\bar{X}\) 去估计之. 如要估计的是参数 \(\lambda\) 本身, 就用 \(1 \bar{X}\).

另一方面,如在第三章例 2.5 中指出的, 指数分布的方差为

\(s)\) 去估计. 这个估计与 \(\bar{X}\) 哪个更好? 这就是需要研究的问题, 见下 节。

例 2.3 设 \(X_{1}, \cdots, X_{n}\) 是从区间 \(\left[\theta_{1}, \theta_{2}\right]\) 上均匀分布的总体 中抽出的样本,要估计 \(\theta_{1}, \theta_{2}\).

前已指出 (见第三章例 1.3 和例 2.5). 这总体分布的均值、方 差分别为 \(\left(\theta_{1}+\theta_{2}\right) / 2\) 和 \(\left(\theta_{2}-\theta_{1}\right)^{2} / 12\). 因此按矩法, 建立方程

\[ \bar{X}=\left(\theta_{1}+\theta_{2}\right) / 2, m_{2}=\left(\theta_{2}-\theta_{1}\right)^{2} / 12 \]

得出 \(\theta_{1}, \theta_{2}\) 的解 \(\hat{\theta}_{1}, \hat{\theta}_{2}\) 分别为

\[ \hat{\theta}_{1}=\bar{X}-\sqrt{3 m_{2}}, \hat{\theta}_{2}=\bar{X}+\sqrt{3 m_{2}} \]

也可以用 \(s\) 代替 \(\sqrt{m_{2}}\).

例 2.4 在第三章 \((2.8),(2.9)\) 式中曾定义了分布的偏度系 数 \(\beta_{1}=\frac{\mu_{3}}{\mu_{2}^{3 / 2}}\) 及峰度系数 \(\beta_{2}=\frac{\mu_{4}}{\mu_{2}^{2}}\) (或 \(\beta_{2}-3\) ), 并阐述了它的意义. 根 据矩法, 这些量可分别用 \(\frac{m_{3}}{m_{2}^{3 / 2}}\) 和 \(\frac{m_{4}}{m_{2}^{2}}\) 去估计之.

本例与前几例不同之处在于: 它并不要求总体分布有特定的 参数形式, 如正态分布, 指数分布之类. 总体分布为任何分布都可 以, 只要其三阶 (对 \(\beta_{1}\) ) 或四阶 (对 \(\beta_{2}\) ) 矩存在就行. 凡是被估计的 对象能直接用矩表达出来时, 都属于这种情况, 其中最重要的例子 是均值方差. 只要总体分布的均值方差存在, 则总可以用样本均值 \(\bar{X}\) 或样本方差 \(S^{2}\) 去估计之, 而不论其分布有如何的形式. 不过, 在 总体分布已知有某种参数形式时, 总体的均值方差也可以有比 \(\bar{X}\) 或 \(S^{2}\) 更好的估计(见后面有关的例子).

例 2.5 设总体有二项分布 \(B(N, p), X_{1}, \cdots, X_{n}\) 为从该总 体中抽出的样本. 要估计 \(p\), 矩估计为 \(\bar{X} / N\).

例 2.6 设总体有波哇松分布 \(P(\lambda), X_{1}, \cdots, X_{n}\) 为从该总体 中抽出的样本, 要估计 \(\lambda\).

由于 \(\lambda\) 是总体分布的均值, 按矩估计法, 用样本均值 \(\bar{X}\) 去估计 之; 另一方面, \(\lambda\) 也是总体分布的方差, 故按矩法, 也可以用 \(m_{2}\) 或 \(S^{2}\) 去估计. 这又有一个优劣的问题. 对本例及例 2.2 来说, 在合理 的准则下, 都可以证明用样本均值 \(\bar{X}\) 为优. 在一般情况下通常总是 采取这样的原则: 能用低阶矩处理的就不用高阶矩。

0.3. 3 极大似然估计法

设总体有分布 \(f\left(X ; \theta_{1}, \cdots, \theta_{k}\right), X_{1}, \cdots, X_{n}\) 为自这总体中抽 出的样本, 则样本 \(\left(X_{1}, \cdots, X_{n}\right)\) 的分布 (即其概率密度函数或概率 函数) 为

\[ f\left(X_{1} ; \theta_{1}, \cdots, \theta_{k}\right) f\left(X_{2} ; \theta_{1}, \cdots, \theta_{k}\right) \cdots f\left(X_{n} ; \theta_{1}, \cdots, \theta_{k}\right) \]

记之为 \(L\left(X_{1}, \cdots, X_{n} ; \theta_{1}, \cdots, \theta_{k}\right)\).

固定 \(\theta_{1}, \cdots, \theta_{k}\) 而看作是 \(X_{1}, \cdots, X_{n}\) 的函数时, \(L\) 是一个概率 密度函数或概率函数, 可以这样理解: 若 \(L\left(Y_{1}, \cdots, Y_{n} ; \theta_{1}, \cdots, \theta_{k}\right)\) \(>L\left(X_{1}, \cdots, X_{n} ; \theta_{1}, \cdots, \theta_{k}\right)\), 则在观察时出现 \(\left(Y_{1}, \cdots, Y_{n}\right)\) 这个点 的可能性, 要比出现 \(\left(X_{1}, \cdots, X_{n}\right)\) 这个点的可能性大. 把这件事反 过来说, 可以这样想: 当已观察到 \(X_{1}, \cdots, X_{n}\) 时, 若 \(L\left(X_{1}, \cdots, X_{n}\right.\); \(\left.\theta^{\prime}{ }_{1}, \cdots, \theta^{\prime}{ }_{k}\right)>L\left(X_{1}, \cdots, X_{n} ; \theta^{\prime \prime}{ }_{1}, \cdots, \theta_{k}^{\prime \prime}\right)\), 则被估计的参数 \(\left(\theta_{1}\right.\), \(\left.\cdots, \theta_{k}\right)\) 是 \(\left(\theta_{1}^{\prime}, \cdots, \theta_{k}^{\prime}\right)\) 的可能性, 要比它是 \(\left(\theta_{1}^{\prime \prime}, \cdots, \theta_{k}^{\prime \prime}\right)\) 的可能性大.

当 \(X_{1}, \cdots, X_{n}\) 固定而把 \(L\) 看作 \(\theta_{1}, \cdots, \theta_{k}\) 的函数时,它称为 “似然函数”. 这名称的意义, 可根据上述分析得到理解: 这函数对 不同的 \(\left(\theta_{1}, \cdots, \theta_{k}\right)\) 的取值, 反映了在观察结果 \(\left(X_{1}, \cdots, X_{n}\right)\) 已知的 条件下, \(\left(\theta_{1}, \cdots, \theta_{k}\right)\) 的各种值的“似然程度”. 注意这里有些像贝叶 斯公式中的推理 (见第一章 (3.18) 式): 把观察值 \(X_{1}, \cdots, X_{n}\) 看成 结果而参数值 \(\left(\theta_{1}, \cdots, \theta_{k}\right)\) 看成是导致这结果的原因. 现已有了结 果, 要反过来推算各种原因的概率. 这里参数 \(\theta_{1}, \cdots, \theta_{k}\) 有一定的 值 (虽然末知), 并非事件或随机变量, 无概率可言, 于是就改用“似 然”这个词。

从上述分析就自然地导致如下的方法: 应该用似然程度最大 的那个点 \(\left(\theta_{1}^{*}, \cdots, \theta_{k}^{*}\right)\), 即满足条件

\[ \begin{aligned} & L\left(X_{1}, \cdots, X_{n} ; \theta_{1}^{*}, \cdots, \theta_{k}^{*}\right) \\ & \quad=\max _{\theta_{1}, \cdots, \theta_{k}} L\left(X_{1}, \cdots, X_{n} ; \theta_{1}, \cdots, \theta_{k}\right) \end{aligned} \]

的 \(\left(\theta_{1}^{*}, \cdots, \theta_{k}^{*}\right)\) 去作为 \(\left(\theta_{1}, \cdots, \theta_{k}\right)\) 的估计值, 因为在已得样本 \(X_{1}\), \(\cdots, X_{n}\) 条件下, 这个 “看来最像” 是真参数值. 这个估计 \(\left(\theta_{1}^{*}, \cdots\right.\), \(\left.\theta_{k}^{*}\right)\) 就叫做 \(\left(\theta_{1}, \cdots, \theta_{k}\right)\) 的 “极大似然估计”. 如果要估计的是 \(g\left(\theta_{1}\right.\), \(\left.\cdots, \theta_{k}\right)\), 则 \(g\left(\theta_{1}^{*}, \cdots, \theta_{k}^{*}\right)\) 是它的极大似然估计.

因为

\[ \log L=\sum_{i=1}^{n} \log f\left(X_{i} ; \theta_{1}, \cdots, \theta_{k}\right) \]

且为使 \(L\) 达到最大, 只须使 \(\log L\) 达到最大, 故在 \(f\) 对 \(\theta_{1}, \cdots, \theta_{k}\) 存 在连续的偏导数时, 可建立方程组 (称为似然方程组):

\[ \frac{\partial \log L}{\partial \theta_{i}}=0, i=1, \cdots, \dot{k} \]

如果这方程组有唯一的解, 又能验证它是一个极大值点, 则它必是 使 \(L\) 达到最大之点, 即极大似然估计. 在几个常见的重要例子中 这一点不难验证. 可是, 在较复杂的场合, 方程组 (2.5) 可以有不止 一组解, 求出这些解很费计算, 且不易判定那一个使 \(L\) 达到最大.

有时, 函数 \(f\) 并不对 \(\theta_{1}, \cdots, \theta_{k}\) 可导, 甚至 \(f\) 本身也不连续,这 时方程组 (2.5) 就无法用, 必须回到原始的定义 2.3.

现举一些例子来说明求极大似然估计的过程.

例 2.7 设 \(X_{1}, \cdots, X_{n}\) 是从正态总体 \(N\left(\mu, \sigma^{2}\right)\) 中抽出的样 本, 则似然函数为

\[ \begin{aligned} L & =\prod_{i=1}^{n}\left[\left(\sqrt{2 \pi \sigma^{2}}\right)^{-1} \exp \left(-\frac{1}{2 \sigma^{2}}\left(X_{i}-\mu\right)^{2}\right)\right] \\ \log L & =-\frac{n}{2} \log (2 \pi)-\frac{n}{2} \log \left(\sigma^{2}\right)-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2} \end{aligned} \]

求方程组 (2.5) (把 \(\sigma^{2}\) 作为一个整体看):

\[ \begin{gathered} \frac{\partial \log L}{\partial \mu}=\frac{1}{\sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-\mu\right)=0 \\ \frac{\partial \log L}{\partial\left(\sigma^{2}\right)}=-\frac{n}{2 \sigma^{2}}+\frac{1}{2 \sigma^{4}} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}=0 \end{gathered} \]

由第一式得出 \(\mu\) 的解为

\[ \mu^{*}=\sum_{i=1}^{n} X_{i} / n=\bar{X} \]

以此代入第二式的 \(\mu\),得到 \(\sigma^{2}\) 的解为

\[ \sigma^{* 2}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} / n=m_{2} \]

我们看到: \(\mu\) 与 \(\sigma^{2}\) 的极大似然估计 \(\mu^{*}\) 和 \(\sigma^{* 2}\), 与其矩估计完全一 样. 在本例中, 容易肯定 \(\left(\mu^{*}, \sigma^{* 2}\right)\) 确是使似然函数 \(L\) 达得最大值 之点. 因为, 似然方程组只有唯一的根 \(\left(\mu^{*}, \sigma^{* 2}\right)\), 而这个点不可 能是 \(L\) 的极小值点. 因为, 由 \(L\) 的表达式 (2.6) 可知, 当 \(|\mu| \rightarrow \infty\) 或 \(\sigma^{2} \rightarrow 0\) 时, \(L\) 趋向于 0 , 而 \(L\) 在每个点处都大于 0 . 以下几个例 子都可以按照这个方式去验证, 我们就不一一重复了.

例 2.8 设 \(X_{1}, \cdots, X_{n}\) 是从指数分布总体中抽出的样本, 求 参数 \(\lambda\) 的极大似然估计.

有

\[ L=\prod_{i=1}^{n}\left(\lambda \mathrm{e}^{-\lambda x_{i}}\right) \]

故

\[ \log L=n \log \lambda-\lambda \sum_{i=1}^{n} X_{i} \]

解方程

\[ \frac{\partial \log L}{\partial \lambda}=\frac{n}{\lambda}-\sum_{i=1}^{n} X_{i}=0 \]

得 \(\lambda\) 的极大似然估计为

\[ \lambda^{*}=n / \sum_{i=1}^{n} X_{i}=1 / \bar{X} \]

仍与其矩估计一样. 但是在这里, 极大似然估计只有一个, 而如在 例 2.2 中所指出的, \(\lambda\) 的矩估计依使用不同阶的矩, 可以有几个.

例 2.9 设 \(X_{1}, \cdots, X_{n}\) 是从均匀分布 \(R(0, \theta)\) 的总体中抽出 的样本, 求 \(\theta\) 的极大似然估计.

\(X_{i}\) 的密度函数为 \(1 / \theta\), 当 \(0<X_{i}<\theta\), 此外为 0 . 故似然函数 \(L\) 为

\[ L= \begin{cases}\theta^{-n}, & \text { 当 } 0<X_{i}<\theta, i=1, \cdots, n \\ 0, & \text { 其他情况 }\end{cases} \]

对固定的 \(X_{1}, \cdots, X_{n}\), 此函数为 \(\theta\) 的间断函数,故无法使用似然方 程 (2.5). 但此例不难直接用最初的定义 2.3 去解决: 为使 \(L\) 达到 最大, \(\theta\) 必须尽量小, 但又不能太小以致 \(L\) 为 0 . 这界线就在 \(\theta^{*}=\) \(\max \left(X_{1}, \cdots, X_{n}\right)\) 处: 当 \(\theta \geqslant \theta^{*}\) 时, \(L\) 大于 0 且为 \(\theta^{-n}\). 当 \(\theta<\theta^{*}\) 时, \(L\) 为 0 . 故唯一使 \(L\) 达到最大的 \(\theta\) 值, 即 \(\theta\) 的极大似然估计, 为 \(\theta^{*}\).

如果用矩估计法, 则因总体分布的均值为 \(\theta / 2, \theta\) 的矩估计为 \(\hat{\theta}=2 \bar{X}\). 这两个估计的优劣比较将在后面讨论.

例 2.10 再考虑例 2.5, 有

\[ \begin{gathered} L=\prod_{i=1}^{n}\left[\left(\begin{array}{l} N \\ X_{i} \end{array}\right) p^{\left.X_{i}(1-p)^{N-X_{i}}\right]}\right. \\ \log L=\sum_{i=1}^{n} \log \left(\begin{array}{l} N \\ X_{i} \end{array}\right)+\sum_{i=1}^{n} X_{i} \log p+\sum_{i=1}^{n}\left(N-X_{i}\right) \log (1-p) \end{gathered} \]

作方程

\[ \frac{\partial \log L}{\partial p}=\frac{1}{p} \sum_{i=1}^{n} X_{i}-\left(n N-\sum_{i=1}^{n} X_{i}\right) \frac{1}{1-p}=0 \]

此方程之解, 即 \(p\) 的极大似然估计, 为 \(p^{*}=\bar{X} / N\), 与矩估计相 同.

例 2.11考虑例 2.6. 容易证明: \(\lambda\) 的极大似然估计 \(\lambda^{*}=\bar{X}\), 与短估计相同.

在我们所举的这些例子中（这些例子都是在应用上最常见 的),矩估计与极大似然估计在多数情况下一致。这更多地是一种 巧合, 并非一般情形. 有意思的是: 在这些例子中这两种估计方法 结果一致,说明这些估计是良好的. 这一点当然还需要一定的理论 证明.

也有这样的情况, 用这两个估计方法都行不通或不易实行.下 面是一个例子.

例 2.12 设总体分布有密度函数

\[ f(x, \theta)=\frac{1}{\pi\left[1+(x-\theta)^{2}\right]},-\infty<x<\infty \]

这分布包含一个参数 \(\theta, \theta\) 可取任何实数值. 这分布叫柯西分布, 其密度作为 \(x\) 的函数, 关于 \(\theta\) 点对称. 故 \(\theta\) 是这个分布的中位数 （见第三章 3.1.4).

现设 \(X_{1}, \cdots, X_{n}\) 为自这总体中抽出的样本, 要估计 \(\theta\). 由于

\[ \int_{-\infty}^{\infty}|x| f(x, \theta) \mathrm{d} x=\infty \]

柯西分布的一阶矩也不存在, 更不用说更高阶的矩了. 因此, 矩估 计无法使用. 若用极大似然法,则将得出方程

\[ \sum_{i=1}^{n} \frac{X_{i}-\theta}{1+\left(X_{i}-\theta\right)^{2}}=0 \]

这方程有许多根且求根不容易. 因此, 对本例而言, 极大似然法也 不是理想的方法.

为估计参数 \(\theta\), 有一个较简单易行但看来合理的方法可用.这 个方法是基于 \(\theta\) 是总体分布的中位数这个事实. 既如此,我们就 要设法在样本 \(X_{1}, \cdots, X_{n}\) 中找一种对应于中位数的东西.这个思 想其实在矩估计法中就已用过，因为总体矩在样本中的对应物就 是样本矩. 现在把 \(X_{1}, \cdots, X_{n}\) 按由小到大排成一列:

\[ X_{(1)} \leqslant X_{(2)} \leqslant \cdots \leqslant X_{(n)} \]

它们称为次序统计量. 既然中位数是 “居中”的意思, 我们就在样本 中找居中者:

\[ \hat{m}=\left\{\begin{array}{l} X_{((n+1) / 2)}, \text { 当 } n \text { 为奇数时 } \\ \left(X_{(n / 2)}+X_{(n / 2+1)}\right) / 2, \text { 当 } n \text { 为偶数时 } \end{array}\right. \]

当 \(n\) 为奇数时, 有一个居中者为 \(X_{((n+1) / 2)}\); 若 \(n\) 为偶然, 就没有 一个居中者, 就把两个最居中者取平均, 这样定义的 \(\hat{m}\) 叫作“样本 中位数”. 我们就拿 \(\hat{m}\) 作为 \(\theta\) 的估计.

就正态总体 \(N\left(\mu, \sigma^{2}\right)\) 而言, \(\mu\) 也是总体的中位数,故 \(\mu\) 也可 以用样本中位数去估计. 从这些例子中, 我们看出一点: 统计推断 问题的解, 往往可以从许多看来都合理的途径去考虑,并无一成不 变的方法,不同解固然有优劣之分, 但这种优劣也是相对于一定的 准则而言. 并无绝对的价值.下述情况也并非不常见: 估计甲在某 一准则下优于乙, 而乙又在另一准则下优于甲.

极大似然估计法的思想,始于高斯的误差理论,到 1912 年由 R. A. 费歇尔在一篇论文中把它作为一个一般的估计方法提出 来. 自 20 年代以来,费歇尔自己及许多统计学家对这一估计法进 行了大量的研究. 总的结论是: 在各种估计方法中, 相对说它一般 更为优良, 但在个别情况下也给出很不理想的结果. 与矩估计法不 同, 极大似然估计法要求分布有参数的形式. 比方说, 如对总体分 布毫无所知而要估计其均值方差, 极大似然法就无能为力.

0.4. 4 贝叶斯法

贝叶斯学派是数理统计学中的一大学派. 在这一段中,我们简 略地介绍一下这个学派处理统计问题的基本思想.

拿我们目前讨论的点估计问题来说，无论你用矩估计也好，用 极大似然估计或其他方法也好,在我们心目中, 末知参数 \(\theta\) 就简 单地是一个末知数, 在抽取样本之前, 我们对 \(\theta\) 没有任何了解, 所 有的信息全来自样本.

贝叶斯学派则不然, 它的出发点是: 在进行抽样之前, 我们已 对 \(\theta\) 有一定的知识, 叫做先验知识. 这里 “先验” 的意思并非先验 论, 而只是表示这种知识是“在试验之先”就有了的,也有人把它叫 做验前知识, 即“在试验之前”的意思。

贝叶斯学派进一步要求:这种先验知识必须用 \(\theta\) 的某种概率 分布表达出来,这概率分布就叫做 \(\theta\) 的“先验分布”或“验前分 布”. 这个分布总结了我们在试验之前对末知参数 \(\theta\) 的知识.

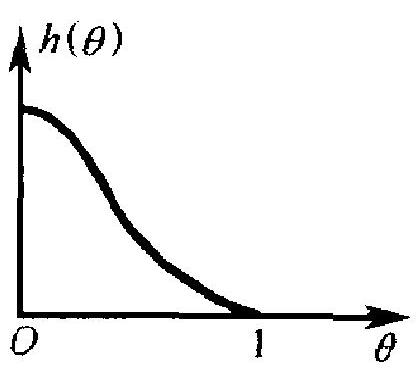
举一个例子. 设某工厂每日生产一大批某种产品,我们想要估 计当日的废品率 \(\theta\). 该厂在以前已生产过很多批产品,如果过去的 检验有记录在,则它确实提供了关于废品率 \(\theta\) 的一种有用信息, 据此可以画出 \(\theta\) 的密度曲线, 如图 4.1(a), (b).

(a)

(b)

图 4.1

图中 \(h(\theta)\) 表示 \(\theta\) 的密度函数, \(0 \leqslant \theta \leqslant 1\). (a)表示一个较好的 情况: \(h(\theta)\) 在 \(\theta=0\) 附近很大而当 \(\theta\) 增加时,下降很快.这表示该 厂以往的废品率通常都很低. (b)则表示一个不大好的情况: 比较 大的废品率出现的比率相当高. 容易理解: 这种关于 \(\theta\) 的历史知 识 (即先验知识), 在当前估计废品率 \(\theta\) 时, 应适当地加以使用而 不应弃之不顾.这种思想与我们日常处事的习惯符合 : 当我们面临 一个问题时, 除考虑当前的情况外, 往往还要注意以往的先例和经 验。

问题就来了: 如果这个工厂以往没有记录,或甚至是一个新开 工的工厂, 该怎么办? 怎样去获得上文所指的先验密度 \(h(\theta)\) ? 贝 叶斯统计的一个基本要求是: 你必须设法去定出这样一个 \(h(\theta)\), 甚至出于你自己的主观认识 “也可以, 这要成为问题中一个必备 的要素. 正是在这一点上, 贝叶斯统计遭到不少的反对和批评, 而 一个初接触这个问题的人，也容易这样想: “这怎么行? 我没有根 据怎么能凭主观想像去定出一个先验密度 \(h(\theta)\) ”. 关于这一点, 贝 叶斯学派的信奉者有自己的一套说法, 这问题非三言两语能说清 楚. 本书作者有一篇通俗形式的文章 (见《数理统计与应用概率》 1990 年第四期, p. 389-400), 其中对这个问题及有关问题作了仔 细说明, 有兴趣的读者可以参考.

现在我们转到下一个问题: 已定下了先验密度之后, 怎样去得 出参数 \(\theta\) 的估计.

设总体有概率密度 \(f(X, \theta)\) (或概率函数,若总体分布为离散 的), 从这总体抽样本 \(X_{1}, \cdots, X_{n}\), 则这样本的密度为 \(f\left(X_{1}, \theta\right) \cdots f\) \(\left(X_{n}, \theta\right)\). 它可视为在给定 \(\theta\) 值时 \(\left(X_{1}, \cdots, X_{n}\right)\) 的密度，根据第二章 (3.5) 式及该式下的一段说明, \(\left(\theta, X_{1}, \cdots, X_{n}\right)\) 的联合密度为

\[ h(\theta) f\left(X_{1}, \theta\right) \cdots f\left(X_{n}, \theta\right) \]

由此,算出 \(\left(X_{1}, \cdots, X_{n}\right)\) 的边缘密度为

\[ p\left(X_{1}, \cdots, X_{n}\right)=\int h(\theta) f\left(X_{1}, \theta\right) \cdots f\left(X_{n}, \theta\right) \mathrm{d} \theta \]

积分的范围, 要看参数 \(\theta\) 的范围而定. 如上例 \(\theta\) 为废品率, 则 \(0 \leqslant \theta\) \(\leqslant 1\). 若 \(\theta\) 为指数分布中的参数 \(\lambda\), 则 \(0<\theta<\infty\), 等等. 由(2.10), 再 根据第二章的公式 (3.4), 得到在给定 \(X_{1}, \cdots, X_{n}\) 的条件下, \(\theta\) 的 条件密度为

\[ h\left(\theta \mid X_{1}, \cdots, X_{n}\right)=h(\theta) f\left(X_{1}, \theta\right) \cdots f\left(X_{n}, \theta\right) / p\left(X_{1}, \cdots, X_{n}\right) \]

照贝叶斯学派的观点, 这个条件密度代表了我们现在 (即在取得样 本 \(X_{1}, \cdots, X_{n}\) 后) 对 \(\theta\) 的知识, 它综合了 \(\theta\) 的先验信息 (以 \(h(\theta)\) 反 映) 与由样本带来的信息. 通常把 (2.11) 称为 \(\theta\) 的 “后验 (或验后)

• 就是说, 这里允许使用主观概率, 见第一章 1.1 节 密度”, 因为他是在做了试验以后才取得的.

如果把上述过程和我们在第一章中讲过的贝叶斯公式相比, 就可以理解: 现在我们所做的, 可以说不过是把贝叶斯公式加以 “连续化”而已,看下表中的比较。

	问 题	先验知识	当前知识	后验 (现在) 知识
闪叶斯公式	\(\begin{array}{l}\text { 事 件 } B_{1}, \cdots, B_{n} \\ \text { 中那一个发生了? }\end{array}\)	\(\begin{array}{l}P\left(B_{1}\right), \\ \cdots, P\left(B_{n}\right)\end{array}\)	事件 \(A\) 发生了	\(\begin{array}{l}P\left(B_{1} \mid A\right), \cdots, \\ P\left(B_{n} \mid A\right)\end{array}\)
此处的问题	\(\theta=?\)	\(h(\theta)\)	样本 \(X_{1}, \cdots, X_{n}\)	后猃密度 (2.11)

由这里我们就理解到: 为什么一个看来不起眼的贝叶斯公式会有 如此大的影响. 这一点我们在第一章中已有所论述了.

贝叶斯学派的下一个重要观点是: 在得出后验分布 (2.11)后, 对参数 \(\theta\) 的任何统计推断, 都只能基于这个后验分布. 至于具体 如何去使用它, 可以结合某种准则一起去进行, 统计学家也有一定 的自由度. 拿此处讨论的点估计问题来说, 一个常用的方法是: 取 后验分布 (2.11) 的均值作为 \(\theta\) 的估计.

还有一点需要说明一下: 按上文, \(h(\theta)\) 必须是一个密度函数, 即必须满足 \(h(\theta) \geqslant 0, \int h(\theta) \mathrm{d} \theta=1\) 这两个条件. 但在有些情况 下, \(h(\theta) \geqslant 0\), 但 \(\int h(\theta) \mathrm{d} \theta\) 不为 1 甚至为 \(\infty\), 不过积分 (2.10) 仍有 限, 这时, 由 (2.11) 定义的 \(h\left(\theta \mid X_{1}, \cdots, X_{n}\right)\) 作为 \(\theta\) 的函数, 仍满足 密度函数的条件. 这就是说, 即使这样的 \(h(\theta)\) 取为先验密度也无 妨. 当然, 由于 \(\int h(\theta) \mathrm{d} \theta\) 不为 1 , 它已失去了密度函数的通常的概 率意义. 这样的 \(h(\theta)\) 通常称为“广义先验密度”。

例 2.13 作 \(n\) 次独立试验, 每次观察某事件 \(A\) 是否发生, \(A\) 在每次试验中发生的概率为 \(p\), 要依据试验结果去估计 \(p\).

这问题我们以往就“用频率估计概率”的方法去处理 (这也是 它的矩估计与极大似然估计). 这方法不用 \(p\) 的先验知识. 现在我 们用贝叶斯统计的观点来处理这个问题.

引进 \(X_{i}=1\) 或 0 ,视第 \(i\) 次试验时 \(A\) 发生与否而定, \(i=1, \cdots\), \(n \cdot P\left(X_{i}=1\right)=p, P\left(X_{i}=0\right)=1-p\). 因此 \(\left(X_{1}, \cdots, X_{n}\right)\) 的概率函 数为 \(p^{x}(1-p)^{n-x}, X=\sum_{i=1}^{n} X_{i}\). 取 \(p\) 的先验密度 \(h(p)\), 则 \(p\) 的 后验密度为

\[ \begin{aligned} & h\left(p \mid X_{1}, \cdots, X_{n}\right) \\ = & h(p) p^{x}(1-p)^{n-x} / \int_{0}^{1} h(p) p^{x}(1-P)^{n-x} \mathrm{~d} p, 0 \leqslant p \leqslant 1 \end{aligned} \]

此分布的均值为

\[ \begin{aligned} \widetilde{p} & =\widetilde{p}\left(X_{1}, \cdots, X_{n}\right)=\int_{0}^{1} p h\left(P \mid X_{1}, \cdots, X_{n}\right) \mathrm{d} p \\ & =\int_{0}^{1} h(p) p^{x+1}(1-p)^{n-x} \mathrm{~d} p / \int_{0}^{1} h(p) p^{x}(1-p)^{n-x} \mathrm{~d} p \end{aligned} \]

\(\tilde{p}\) 就是 \(p\) 在先验分布 \(h(p)\) 之下的贝叶斯估计.

如何选择 \(h(p)\) ? 贝叶斯本人曾提出“同等无知”的原则，即 事先认为 \(p\) 取 \([0,1]\) 内一切值都有同等可能, 就是说取 \([0,1]\) 内均 匀分布 \(R(0,1)\) 作为 \(p\) 的先验分布. 这时 \(h(p)=1\) 当 \(0 \leqslant p \leqslant 1\), 而 (2.12) 中的两个积分都可以用 \(\beta\) 函数表出 (见第二章 (4.22) 式). 由此得

\[ \tilde{p}=\beta(X+2, n-X+1) / \beta(X+1, n-X+1) \]

根据 \(\beta\) 函数与 \(\Gamma\) 函数的关系式 \((4.25)\), 以及当 \(k\) 为自然数时 \(\Gamma(k)=(k-1) !\), 由 \((2.13)\) 不难得到

\[ \widetilde{p}=(X+1) /(n+2) \]

这个估计与频率 \(X / n\) 有些差别, 当 \(n\) 很大时不显著, 而在 \(n\) 很小 时颇为显著.从一个角度看, 当 \(n\) 相当小时, 用贝叶斯估计 (2.14) 比用 \(X / n\) 更合理. 因为当 \(n\) 很小时, 试验结果可能出现 \(X=0\) 或 \(X=n\) 的情况. 这时, 依 \(X / n\) 应把 \(p\) 估计为 0 或 1 , 这就太极端了 (我们不能仅根据在少数几次试验中 \(A\) 会不出现或全出现, 就判 定它为不可能或必然). 若按 (2.14), 则在这两种情况下分别给出 估计值 \(1 /(n+2)\) 和 \((n+1) /(n+2)\). 这就留有一定的余地.

这个“同等无知”的原则, 又称贝旪斯原则, 被广泛用到一些其 他的情况. 不过随着所估计的参数的范围和性质的不同, 该原则的 具体表现形式也不同.例如,为估计正态分布 \(N\left(\mu, \sigma^{2}\right)\) 中的 \(\mu\),同 等无知原则给出一个广义先验密度 \(h(\mu) \equiv 1\). 若估计 \(\sigma\), 则应取 \(h(\sigma)=\sigma^{-1}(\sigma>0)\). 若估计指数分布中的 \(\lambda\), 则取 \(h(\lambda)=\lambda^{-1}(\lambda\) \(>0)\). 这些都是广义先验密度. 其所以这样做的理由, 不能在此处 细谈了.

这个原则也受到一些批评, 其中最有力的批评是其不确定性. 理由是: 拿本例的 \(p\) 来说, 若对 \(p\) 同等无知, 则对 \(p^{2}\) (或 \(p^{3}, p^{4}, \cdots\) 等)也应是同等无知, 因而也可以把 \(p^{2}\) 的密度函数取为 \(R(0,1)\) 的密度. 这时不难算出 \(p\) 的密度将为 \(h(p)=2 p\) (当 \(0 \leqslant p \leqslant 1\), 其 外为 0 ), 与本例所给不一致. 另外, 不言而喻, 同等无知的原则是 一个在确实没有什么信息时, 不得已而采用的办法. 在实际问题 中, 有时是存在更确实的信息的,如本段开始讲到的那个估计废品 率的情况. 又如,估计一个基本上均匀的铜板在投掷时出现正面的 概率 \(p\). 我们有理由事先肯定 \(p\) 离 \(1 / 2\) 不远. 这时, 可考虑取一个 适当的数 \(\varepsilon>0\), 而把 \(p\) 的先验分布取为 \([1 / 2-\varepsilon, 1 / 2+\varepsilon]\) 内的均 匀分布. 这肯定比用同等无知的原则效果要好, 尤其是在试验次数 \(n\) 不大时.

例 2.14 设 \(X_{1}, \cdots, X_{n}\) 是自正态总体 \(N(\theta, 1)\) 中抽出的样 本. 为估计 \(\theta\), 给出 \(\theta\) 的先验分布为正态分布 \(N\left(\mu, \sigma^{2}\right)\left(\mu, \sigma^{2}\right.\) 当然 都已知). 求 \(\theta\) 的贝叶斯估计. 在本例中有

\[ \begin{aligned} h(\theta) & =(\sqrt{2 \pi} \sigma)^{-1} \exp \left[-\frac{1}{2 \sigma^{2}}(\theta-\mu)^{2}\right] \\ f(x, \theta) & =(\sqrt{2 \pi})^{-1} \exp \left[-\frac{1}{2}(x-\theta)^{2}\right] . \end{aligned} \]

故按公式 (2.11) 知, \(\theta\) 的后验密度为

\[ h\left(\theta \mid X_{1}, \cdots, X_{n}\right)=\exp \left[-\frac{1}{2 \sigma^{2}}(\theta-\mu)^{2}-\frac{1}{2} \sum_{i=1}^{n}\left(X_{i}-\theta\right)^{2}\right] / I \]

其中 \(I\) 是一个与 \(\theta\) 无关而只与 \(\mu, \sigma, X_{1}, \cdots, X_{n}\) 有关的数. 简单的 代数计算表明

\[ -\frac{1}{2 \sigma^{2}}(\theta-\mu)^{2}-\frac{1}{2} \sum_{i=1}^{n}\left(X_{i}-\theta\right)^{2}=-\frac{1}{2 \eta^{2}}(\theta-t)^{2}+J \]

其中

\[ \begin{gathered} t=\left(n \bar{X}+\mu / \sigma^{2}\right) /\left(n+1 / \sigma^{2}\right) \\ \eta^{2}=1 /\left(n+1 / \sigma^{2}\right) \end{gathered} \]

而 \(J\) 与 \(\theta\) 无关. 以(2.16)代人 \((2.15)\), 得

\[ h\left(\theta \mid X_{1}, \cdots, X_{n}\right)=I_{1} \exp \left[-\frac{1}{2 \eta^{2}}(\theta-t)^{2}\right] \]

这里 \(I_{1}=I e^{J}\) 与 \(\theta\) 无关. \(I_{1}\) 不必直接算, 因为, \(h\left(\theta \mid X_{1}, \cdots, X_{n}\right)\) 作 为 \(\theta\) 的函数是一个概率密度函数, 它必须满足条件

\[ \int_{-\infty}^{\infty} h\left(\theta \mid X_{1}, \cdots, X_{n}\right) \mathrm{d} \theta=1 \]

这就决定了 \(I_{1}=(\sqrt{2 \pi} \eta)^{-1}\). 因此, \(\theta\) 的后验分布就是正态分布 \(N\left(t, \eta^{2}\right)\), 其均值 \(t\) 就是 \(\theta\) 的贝叶斯估计 \(\tilde{\theta}\) :

\[ \tilde{\theta}=t=\frac{n}{n+1 / \sigma^{2}} \bar{X}+\frac{1 / \sigma^{2}}{n+1 / \sigma^{2}} \mu \]

把 \(\tilde{\theta}\) 写成 (2.19)的形状很有意思. 设想两个极端情况: 一个是 只有样本信息而毫无先验信息, 这就是我们以前讨论的情况, 这时 用样本均值 \(\bar{X}\) 去估计 \(\theta\). 另一个是只有先验信息 \(N\left(\mu, \sigma^{2}\right)\) 而没有 样本. 这时, 我们只好用先验分布的均值 \(\mu\) 作为 \(\theta\) 的估计. 由 (2.19)式看出 : 当两种信息都存在时, \(\theta\) 的估计为二者的折裔. 它 是上述两个极端情况下的估计 \(\bar{X}\) 和 \(\mu\) 的加权平均, 权之比为 \(n: 1\) / \(\sigma^{2}\). 这个比值很合理: \(n\) 为样本数目, \(n\) 愈大, 样本信息愈多, \(\bar{X}\) 的 权就该更大. 对 \(\mu\) 而言, 其重要性则要看 \(\sigma^{2}\) 的大小. \(\sigma^{2}\) 愈大, 表示 先验信息愈不肯定 ( \(\theta\) 在 \(\mu\) 周围的散布很大). 反之, \(\sigma^{2}\) 很小时, 仅 根据先验信息, 已有很大把握肯定 \(\theta\) 在 \(\mu\) 附近不远处. 因此, \(\mu\) 的 权应与 \(\sigma^{2}\) 成反比. 公式 (2.19)恰好体现了上述分析. 目前在国际统计界及应用统计工作者中, 贝叶斯学派已有很 大影响. 其原因在于它确实有一些别的方法所不具备的优点. 这些 在今后我们还将看到. 在我国, 贝叶斯方法也开始受到重视并得到 一些应用. 对把数理统计学方法作为一种工具的应用工作者来说, 对这个学派的方法有必要有一定的了解.

评论

登录github的账号后，可以直接在下方评论框中输入。

如果想进行更详细的讨论(如排版、上传图片等)，选择一个反应后并点击上方的文字，进入论坛页面。