5.2 重要参数检验

5.2 重要参数检验

本节中我们将讨论几个常用的检验.构造检验, 也有些带一般 性的方法. 但这些方法应用上比较成功的情况, 很大一部分也就是 本节要讲到的几个常用例子. 所以, 我们不采取从介绍这种一般方 法出发再回到具体例子的讲法, 而在每一个具体问题中, 从直观想 法出发去构造看来是合理的检验.

这种直观方法是基于参数的点估计. 原则上很简单: 考虑一个 单参数的情形. 设被检验的原假设是 \(H_{0}: \theta=\theta_{0}\), 或 \(\theta \leqslant \theta_{0}\), 或 \(\theta \geqslant\) \(\theta_{0}\). 有了样本以后, 先找 \(\theta_{0}\) 的一适当的点估计 \(T\). 如果 \(\theta=\theta_{0}\) 成立. 则 \(T\) 与 \(\theta_{0}\) 相去不应太远, 故直观上看, 应当在 \(\left|T-\theta_{0}\right|>\) 某常数 \(C\) 时, 否定 \(H_{0}\), 而在 \(\left|T-\theta_{0}\right| \leqslant C\) 时接受 \(H_{0}\) (也可以两边不对称,故一般也可 以: 在 \(C_{1} \leqslant T \leqslant C_{2}\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\) ). 如果要检验的原假 设是 \(\theta \leqslant \theta_{0}\), 则应当在 \(T>C\) 时否定 \(H_{0}\), 这看起来很简单. 但问题 在于, 我们对检验有一定的水平要求, 上述简单处理有时无法满足 这一要求,而需要在上述基础上作一些修改. 这就没有定规了. 从 以下实例的讨论中,读者会能悟出这里面的问题所在.

本节的另一个任务是通过这些例子的解说, 加深对上节所述 一般概念的理解,并阐明若干在前节没有深人发挥的论点.

0.1. 1 正态总体均值的检验

设 \(X_{1}, \cdots, X_{n}\) 是自正态总体 \(N\left(\theta, \sigma^{2}\right)\) 中抽出的样本, 我们来 讨论有关均值 \(\theta\) 的假设检验问题. 在应用上常见到的形式有 \(\left(\theta_{0}\right.\) 是一给定的数):

\(1^{\circ} H_{0}: \theta \geqslant \theta_{0}, H_{1}: \theta<\theta_{0}\)

\(2^{\circ} \quad H_{0}^{\prime}: \theta \leqslant \theta_{0}, H_{1}^{\prime}: \theta>\theta_{0}\)

\(3^{\circ} \quad H_{0}^{\prime \prime}: \theta=\theta_{0}, H_{1}^{\prime \prime}: \theta \neq \theta_{0}\)

\(H_{0}, H_{0}^{\prime}\) 和 \(H_{0}^{\prime \prime}\) 为原假设, \(H_{1}, H_{1}^{\prime}, H_{1}^{\prime \prime}\) 为对立假设. 以后都按这次 序: 原假设在前.

分两种情况讨论

1. 方差 \(\sigma^{2}\) 已知时

先考虑检验问题 \(1^{\circ}\). 以 \(\bar{X}\) 记样本均值, \(\bar{X}\) 是 \(\theta\) 的估计. 故 \(\bar{X}\) 愈大, 直观上看与原假设 \(H_{0}\) 愈符合. 反之, \(\bar{X}\) 愈小, 则与对立假设 \(H_{1}\) 愈符合. 由此得出一个直观上合理的检验 \(\Phi\) 是

\(\Phi\) : 当 \(\bar{X} \geqslant C\) 时接受原假设 \(H_{0}, \bar{X}<C\) 时否定 \(H_{0}\) (2.1) 要定出常数 \(C\), 使检验有给定水平 \(\alpha\), 为此要考虑 \(\Phi\) 的功效函数 \(\beta_{\Phi}(\theta)\). 按定义 \((1.1)\), 有

\[ \begin{aligned} \beta_{\Phi}(\theta) & =P_{\theta}(\bar{X}<C) \\ & =P_{\theta}(\sqrt{n}(\bar{X}-\theta) / \sigma<\sqrt{n}(C-\theta) / \sigma) \end{aligned} \]

当总体有正态分布 \(N\left(\theta, \sigma^{2}\right)\) 时, \(\sqrt{n}(\bar{X}-\theta) / \sigma\) 服从标准正态分布 \(N(0,1)\). 以 \(\Phi\) 记其分布函数, 有

\[ \beta_{\Phi}(\theta)=\Phi(\sqrt{n}(C-\theta / \sigma) \]

当 \(\theta\) 增加时, \(\sqrt{n}(C-\theta) / \sigma\) 下降, 故 \(\beta_{\Phi}(\theta)\) 也下降, 这样一来, 要 使 \(\beta_{\Phi}(\theta) \leqslant\left(\alpha\right.\) 当 \(\theta \geqslant \theta_{0}\) 时) 只要 \(\beta_{\Phi}\left(\theta_{0}\right)=\alpha\) 即可. 按记号 \(u_{\alpha}\) 的定 义(见第四章 (4.3) 式), 应取 \(C\) 满足 \(\sqrt{n}\left(C-\theta_{0}\right) / \sigma=u_{1-\alpha}=-u_{a}\), 由此得

\[ C=\theta_{0}-\sigma u_{\alpha} / \sqrt{n} \]

(2.1) 和 (2.3) 结合决定了检验 \(\Phi\). 以 \(C\) 代人 (2.2), 得到 \(\Phi\) 的功 效函数为

\[ \beta_{\Phi}(\theta)=\Phi\left(\sqrt{n}\left(\theta_{0}-\dot{\theta}\right) / \sigma-u_{\alpha}\right) \]

当 \(\theta<\theta_{0}\) 即属于对立假设 \(H_{1}\) 时, \(\beta_{\Phi}(\theta)\) 愈大愈好.怎样才能 使 \(\beta_{\Phi}(\theta)\) 大呢? 从公式 (2.4) 分析, 并军记分布函数是非降的,易 得出以下几条结论:

(a) \(\theta\) 愈小, \(\beta_{\Phi}(\theta)\) 愈大. 直观的解释是: \(\theta\) 愈小, 则离原假设 \(H_{0}\) 愈远, 愈易和原假设分辨开, 即犯错误 (第二类) 的概率应愈 小, 因而 \(\beta_{\Phi}(\theta)\) 应愈大. 当 \(\theta<\theta_{0}\) 但 \(\theta\) 接近 \(\theta_{0}\) 时, \(\beta_{\Phi}(\theta) \approx \alpha\). 由于 \(\alpha\) 一般是很小的数, 这时犯第二类错误的概率 \(1-\beta_{\Phi}(\theta) \approx 1-\alpha\) 很接近 1 .

(b)对固定的 \(\theta<\theta_{0}, \sigma\) 愈大, \(\beta_{\Phi}(\theta)\) 愈小. 直观的解释是: \(\sigma\) 愈 大,表示误差的方差愈大. \(\theta\) 与 \(\theta_{0}\) 的差别被“淹没”在误差中,不易 被检出，因而犯错误的概率就大了.正如一杆科误差愈大,愈不易 分别出两件其重量略有不同的物件孰轻孰重.反之, \(\sigma\) 愈小, \(\beta_{\Phi}(\theta)\) 愈大,表示 \(\theta\) 与 \(\theta_{0}\) 的差别愈易检出.

(c) \(\alpha\) 愈大, 则 \(u_{\alpha}\) 愈小, 而 \(\beta_{\Phi}(\theta)\) 就愈大. 直观上的解释是: \(\alpha\) 愈大, 表示能容许的第一类错误概率增大, 这时, 作为补偿, 第二类 错误的概率应有所降低, 即 \(\beta_{\Phi}(\theta)\) 应增加. 这里明白看出两种错误 概率的矛盾关系.

如果我们提出要求: “犯第二种错误的概率要小于指定的 \(\beta>\) 0 ”, 该怎么办? 这等于要求

\[ \beta_{\Phi}(\theta) \geqslant 1-\beta, \theta<\theta_{0} \]

但是, 当 \(\theta<\theta_{0}\) 但 \(\theta\) 接近 \(\theta_{0}\) 时, \(\beta_{\Phi}(\theta) \approx \alpha\), 而因为 \(\alpha, \beta\) 都很小, 一 般有 \(\alpha<1-\beta\). 这就看出: 要求 (2.5) 无法达到. 我们只能放松一 点,要求对某个指定的 \(\theta_{1}<\theta_{0}\), 有

\[ \beta_{\Phi}(\theta) \geqslant 1-\beta \text {, 当 } \theta \leqslant \theta_{1} \]

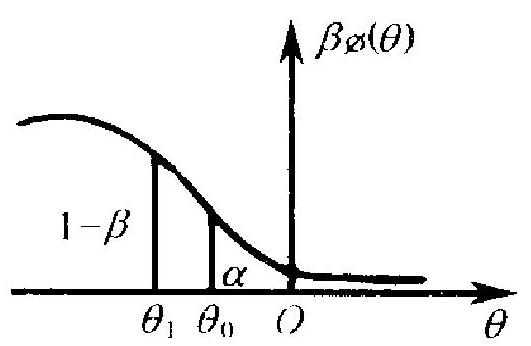
图 5.2

因为 \(\beta_{\Phi}(\theta)\) 随 \(\theta\) 增加而下降 (图 5.2). (2.6) 等价于要求

\[ \beta_{\Phi}\left(\theta_{1}\right) \geqslant 1-\beta \]

按 \((2.4)\), 此即

\[ \Phi\left(\sqrt{n}\left(\theta_{0}-\theta_{1}\right) / \sigma-u_{\alpha}\right) \geqslant 1-\beta \]

或者说 \(\sqrt{n}\left(\theta_{0}-\theta_{1}\right) / \sigma-u_{\alpha} \geqslant u_{\beta}\), 即

\[ n \geqslant \sigma^{2}\left(u_{\alpha}+u_{\beta}\right)^{2} /\left(\theta_{0}-\theta_{1}\right)^{2} \]

就是说, 样本大小至少应达到(2.8) 右边那么大. 例如, 若 \(\sigma^{2}=1\), \(a=\beta=0.05, \theta_{0}-\theta_{1}=0.5\), 则

\[ n \geqslant(1.96+1.96)^{2} /(0.5)^{2}=61.4656, n \geqslant 62 \]

即样本大小至少为 62. (2.6) 式中 \(\theta_{1}\) 的选择, 当然要看实际需要 面定. 它表示, 只有对 \(\theta_{1}\) 及比 \(\theta_{1}\) 更小的值来说, 否定“ “ \(\theta \geqslant \theta_{0}\) ” 才是 要紧的, (2.8)式中 \(n\) 与 \(\sigma^{2}\) 成正比, 即当方差 \(\sigma^{2}\) 愈大时, 为达到一 定的分辨率 (在此可以用 \(\left|\theta_{0}-\theta_{1}\right|\) 来刻画), 所需要的样本数也愈 多.

对检验问题 \(2^{\circ}\), 仿照上述讨论, 容易得出基于检验统计量 \(\bar{X}\) 的检验是

\[ \begin{gathered} \Phi^{\prime} \text { : 当 } \bar{X} \leqslant \theta_{0}+\sigma u_{a} / \sqrt{n} \text { 时接受 } H_{0}^{\prime}: \theta \leqslant \theta_{0}, \\ \text { 不然就否定 } H_{0}^{\prime} \end{gathered} \]

此检验的水平为 \(\alpha\), 功效函数为

\[ \beta^{\prime}{ }_{\Phi}(\theta)=1-\Phi\left(\sqrt{n}\left(\theta_{0}-\theta\right) / \sigma+u_{\alpha}\right) \]

若选定 \(\theta_{1}>\theta_{0}\), 而要求 \(\beta_{\Phi}^{\prime}(\theta) \geqslant 1-\beta\) 当 \(\theta \geqslant \theta_{1}\), 则得最小所需样 本大小 \(n\) 仍由 (2.8) 式决定.

如果样本 \(\left(X_{1}, \cdots, X_{n}\right)\) 使得

\[ \theta_{0}-\sigma u_{\alpha} / \sqrt{n} \leqslant \bar{X} \leqslant \theta_{0}+\sigma u_{\alpha} / \sqrt{n} \]

则按检验问题 \(1^{\circ}\) 的提法, 应接受 \(H_{0}: \theta \geqslant \theta_{0}\), 而按 \(2^{\circ}\) 的提法, 则应 接受 \(H_{0}^{\prime}: \theta \leqslant \theta_{0}\). 从常理看这有矛盾. 其实, 这反映了统计推断的 一种特点, 它不是按那种“非此即彼”的逻辑. 这类现象我们以前就 碰到过了: 作一个参数 \(\theta\) 的点估计, 据同一组样本你可以作出若 干不同的估计,讲起来都有其合理性; 作区间估计时, 不仅用不同 的枢轴变量可导出不同的估计, 即使用同一枢轴变量, 界限可以有 不同选择, 置信系数可以有高低, 都可导致不同的区间, 这些我们 都不认为有矛盾. 此处亦然, 关键在于原假设的选定并非任意, 而 要看问题中提法上的“倾向性”. 此语可通过下面的实例来解释.

假定某工厂生产的一种产品, 其质量指标服从正态分布 \(N\left(\theta, \sigma^{2}\right)\), 且假定 \(\sigma^{2}\) 已知. \(\theta\) 为平均质量指标. 设 \(\theta\) 愈大, 质量愈 好, 而 \(\theta_{0}\) 为达到优级的界限. 某商店经常从该厂进货, 商店提出的 条件是按批验收，只有通过原假设 \(\theta \geqslant \theta_{0}\) 的检验的批才被接受.于 是有两种情况:

（1）从过去较长一段时期的记录，商店相信该厂产品质量总 的说是好的, 当然这不排斥偶尔也出现较差的批. 于是它同意把 \(\theta \geqslant \theta_{0}\) 作为原假设并选定一个较低的检验水平 \(\alpha\), 例如 \(\alpha=0.05\) 甚 至 \(\alpha=0.01\). 这样做对工厂有利, 因为这保证了: 优质的批 (即 \(\theta \geqslant\) \(\theta_{0}\) 的批) 只以很低的概率 \(\alpha\) 被拒收, 而非优质的批仍能以不很小 的概率被接收.从商古的角度考志, 他们地认为这样做并非不利: 一则因为该厂产品质量一贯表现好, 故检验可放宽些, 要有很强的 证据 (即 \(\bar{X}<\theta_{0}-\sigma u_{\alpha} / \sqrt{n}\) ) 才否定 \(\theta \geqslant \theta_{0}\). 一则因为, 既然大多数 批质量是优等的, 取较小的 \(\alpha\), 保证了这样的批能以很大的机会通 过检验, 这对商占有利. 又因为质量差的批本来就不多, 即使这样 的批有较大比例混过检验, 影响也不大.

（2）反之, 若以往一段时期的记录表明, 工厂产品质量并不很 好, 这样, 商店就可能坚持以 \(\theta \leqslant \theta_{0}\) 作为原假设, 并选定一较低的 水平 \(\alpha\). 这样做, 表明商店要求要有较强的证据 (即 \(\bar{X}>\theta_{0}+\) \(\left.\sigma u_{\alpha} / \sqrt{n}\right)\) 才能相信这批产品质量为优. 等于说一个人一向表现不 好, 则必须有较显著的好的表现, 才能相信他确有进步. 这样做就 达到了至少把 \(100(1-\alpha) \%\) 的非优批拒之门外的目的.

由此可见 (从以商店为主动的一方看), 同一个问题 (即 \(\theta \geqslant \theta_{0}\) 或否?), 由于对背景的了解不同而采取了不同的态度,具体是通过 选择何者作为原假设来体现, 到这里, 也就不难理解当样本满足 (2.11) 时,两个原假设 \(H_{0}\) 和 \(H_{0}^{\prime}\) 都能接受的表面矛盾: 你产品质 量一贯很好时, 我认为这样本尚末构成这批产品非优的有力证据; 你产品质量一贯不好时, 我认为这同一样本尚末构成这批产品为 优的有力证据. 出发点不同,并无矛盾可言.

最后, 对于检验问题 \(3^{\circ}, H_{0}^{\prime \prime}: \theta=\theta_{0}\) 而 \(H_{1}^{\prime \prime}: \theta \neq \theta_{0}\), 直观上看合 理的检验规则是: 当 \(\theta\) 的估计值 \(\bar{X}\) 离 \(\theta_{0}\) 较远时,否定 \(H_{1}^{\prime \prime}\), 不然就 接受 \(H_{0}^{\prime \prime}\), 即

\[ \Phi^{\prime \prime} \text { : 当 }\left|\bar{X}-\theta_{0}\right| \leqslant C \text { 时接受 } H_{0}^{\prime \prime} \text {, 不然就否定 } H_{0}^{\prime \prime} \]

选择 \(C\), 使检验 \(\Phi^{\prime \prime}\) 有指定的水平 \(\alpha\). 这等于要求

\[ \begin{aligned} 1-\alpha & \left.=P_{\theta_{0}}\left(\mid \bar{X}-\theta_{0}\right) \mid \leqslant C\right) \\ & =P_{\theta_{0}}\left(\left|\sqrt{n}\left(\bar{X}-\theta_{0}\right) / \sigma\right| \leqslant \sqrt{n} C / \sigma\right) \\ & =\Phi(\sqrt{n} C / \sigma)-\Phi(-\sqrt{n} C / \sigma) \\ & =2 \Phi(\sqrt{n} C / \sigma)-1 \end{aligned} \]

即 \(\Phi(\sqrt{n} C / \sigma)=1-\alpha / 2\), 这导出 \(\sqrt{n} C / \sigma=u_{\alpha / 2}\) 或

\[ C=\sigma u_{\alpha \Omega} / \sqrt{n} \]

(2.12) 与(2.13) 结合,决定了 \(\Phi^{\prime \prime}\).

可以证明 (见附录 \(A\) ) : 检验 \(\Phi\) 和 \(\Phi^{\prime}\) 分别是检验问题 \(1^{\circ}, 2^{\circ}\) 的 水平 \(\alpha\) 的一致最优检验. 而 \(\Phi^{\prime \prime}\) 则不然, 它不是检验问题 \(3^{\circ}\) 的水平 \(\alpha\) 一致最优检验. 更有甚者, 可以证明: 检验问题 \(3^{\circ}\) 的一致最优检 验根本不存在. 直观上这一点不难解释: 问题 \(1^{\circ}, 2^{\circ}\) 是所谓“单侧” 的，即对立假设和原假设各据一侧，这时，检验法则只须照顾一头. 而检验问题 \(3^{\circ}\) 是所谓“双侧” 的，即对立假设分据原假设的两边， 它迫使检验法则采取一种折衣的形态, 这就损害了其最优性.

以上我们详尽地讨论了检验们题 \(1^{\circ}-3^{\circ}\) 当 \(j\) 差已知的情况, 在实用上方差一般末知. 我们之所以对这一情况作仔细讨论, 足因 为这个场合足够简单, 使我们有叮能借此对一些重要概念作活清 楚的解释, 以便举一反三. 现在转到第: 个情况的讨论.

1. 方差 \(\sigma^{2}\) 末知时

仍以问题 \(1^{\circ}\) 为例. 这时, 从原则 上: 看, 制定检验 \(\Phi\) (见 (2.1) 式)的想法仍适用, 但困难在于: 由 (2.3) 所决定的常数 C 依赖于 末知参数 \(\sigma\), 无法确定. 这就需要在上述想法的基础上作一定的修 改,如本节开始处所曾提到的.

把由 (2.1) 和 (2.3)决定的检验 \(\Phi\) 改写成等价形式:

\(\Phi\) : 当 \(\sqrt{n}\left(\bar{X}-\theta_{0}\right) / \sigma \geqslant-u_{\alpha}\) 时接受 \(H_{(0}\), 不然就否定 \(H_{0}\)

这里 \(\sigma\) 末知, 我们可考虑用其估计值 \(S\) 代替, 其中 \(S^{2}=\sum_{i=1}^{n}\left(X_{i}-\right.\) \(\bar{X})^{2} /(n-1)\) 为样本方差. 但在用 \(S\) 代替 \(\sigma\) 后, 分布也起了变化: 由正态分布变为自由度 \(n-1\) 的 \(t\) 分布 (当 \(\theta=\theta_{0}\) 时, 见第一章 (4.34) 式), 因而常数 \(u_{a}\) 也要相应改为 \(t_{n-1}(\alpha)\). 经过这一修改, 得到检验:

\(\Phi\) : 当 \(\sqrt{n}\left(\bar{X}-\theta_{0}\right) / S \geqslant-t_{n-1}(\alpha)\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\)

其水平为 \(\alpha\). 要证明这一点, 就得考虑检验 \(\psi\) 的功效函数

\[ \beta_{\psi}(\theta, \sigma)=P_{\theta, \sigma}\left(\sqrt{n}\left(\bar{X}-\theta_{0}\right) / S<-t_{n-1}(\alpha)\right) \]

可以证明: 这个函数只依赖于 \(\delta=\left(\theta-\theta_{0}\right) / \sigma\), 它是 \(\delta\) 的下降函 数, 且当 \(\delta=0\) 即 \(\theta=\theta_{0}\) 时其值为 \(\alpha\). 这最后 - 条容易证明: 因为当 \(\theta=\theta_{0}\) 时, 统计量 \(\sqrt{n}\left(\bar{X}-\theta_{0}\right) S \sim t_{n-1}\) (第…章 (4.34) 式), 再根据 \(t_{n-1}\) 的密度函数关于 0 对称及记号 \(t_{n-1}(\alpha)\) 的意义, 即有

\[ \beta_{\psi}\left(\theta_{0}, \sigma\right)=P_{\theta_{0}, \sigma}\left(\sqrt{n}\left(\bar{X}-\theta_{0}\right) / S>t_{n \cdot 1}(\alpha)\right)=\alpha \]

利用 \(\beta_{\psi}(\theta, \sigma)\) 是 \(\delta=\left(\theta-\theta_{0}\right) / \sigma\) 的下降函数知, 当 \(\theta>\theta_{0}\) 时即当 \(\delta>0\) 时, \(\beta_{\psi}(\theta, \sigma) \leqslant \beta_{\psi}\left(\theta_{0}, \sigma\right)=\alpha\), 这证明了检验 \(\psi\) 有水平 \(\alpha\). 关于 \(\beta_{4}(\theta, \sigma)\) 只依赖于 \(\delta\) 且是 \(\delta\) 的下降函数的证明, 见附录 \(B\).

类似的论据给出检验问题 \(2^{\circ}\) 和 \(3^{\circ}\) 的水平 \(\alpha\) 检验, 分别记为 \(\psi^{\prime}\) 和 \(\psi^{\prime \prime}\) :

\[ \begin{array}{r} \psi^{\prime} \text { : 当 } \sqrt{n}\left(\bar{X}-\theta_{0}\right) / S \leqslant t_{n-1}(\alpha) \text { 时接受 } H_{0}^{\prime} \text {, 不然就否定 } H_{0}^{\prime} \\ \psi^{\prime \prime} \text { : 当 }\left|\sqrt{n}\left(\bar{X}-\theta_{0}\right) / S\right| \leqslant t_{n-1}(\alpha / 2) \text { 时接受 } H_{0}^{\prime \prime}, \\ \text { 不然就否定 } H_{0}^{\prime \prime}(2.17) \end{array} \]

这三个检验统称为 \(t\) 检验”, 是应用上最重要的检验之一, 由于 \(\sigma\) 末知, 这些检验的性质也就较为复杂. 例如, 不论你怎么指定一个 \(\theta_{1}<\theta_{0}\), 无法找到一个样本大小 \(n\), 使当 \(\theta \leqslant \theta_{1}\) 时, 检验 \(\psi\) 接受 \(H_{0}: \theta \geqslant \theta_{0}\) 的概率, 不超过充分小的 \(\beta>0\) (见附录 \(B\) ), 而在 \(\sigma\) 已知 时这是可以做到的, 又如在 \(\sigma\) 已知时, 单侧检验 \(\Phi\) 和 \(\Phi^{\prime}\) 都是一致 最优的,但 \(\sigma\) 末知时,除非检验水平 \(\alpha \geqslant 1 / 2, t\) 检验 \(\psi\) 和 \(\psi^{\prime}\) 都不是 - 致最优.

例 2.1 两厂生产同一产品, 其质量指标假定都服从正态分 布, 标准规格为均值等于 120 . 现从甲厂抽出 5 件产品, 测得其指 标值为

\[ 119,120,119.2,119.7,119.6 \]

从乙厂也抽出 5 件产品, 测得其指标值为

\[ 110.5,106.3,122.2,113.8,117.2 \]

要根据这些数据去判断该两厂产品是否符合预定规格 120 .

这可以提为假设检验问题 \(\theta=120: \theta \neq 120\), 方差 \(\sigma^{2}\) 末知, 对 甲厂数据, 算出 \(\bar{X}=119.5, S=0.4\), 取 \(\alpha=0.05\), 查表得 \(t_{n-1}(\alpha)\) \(2)=t_{+}(0.025)=2.776\). 有

“更确切些, (2.15)和 (2.16)称为“一样本单侧 \(t\) 检验(一样本表方只有一组样术 \(\left.X_{1}, \cdots, X_{n}\right),(2.17)\) 称为 “一样本双侧 \(t\) 检验”. 有时也把 \(\sigma\) 已知时的检验 \(\Phi, \Phi^{\prime}\) 利 \(\Phi^{\prime \prime}\) 称 为 “ \(u\) 检验”, 但不如 \(t\) 检验的名称用得广”.

\[ \sqrt{n}\left|\bar{X}-\theta_{0}\right| / S=\sqrt{5}|119.5-120| / 0.4=2.795>2.776 \]

对乙厂数据,算出 \(\bar{X}=114, S=6.105\), 而

\[ \sqrt{n}\left|\bar{X}-\theta_{0}\right| / S=\sqrt{5}|114-120| / 6.105=2.198<2.776 \]

故按 0.05 的水平,结论是: 甲厂, 活品与规格不符,但求发现乙厂产 品不符合规格的有力证据.

这个结论可能使不少人感到难以接受. 因为甲厂5 件产品都 与标准值 120 相差很少, 反倒认为不合规格; 而乙厂 5 件中除一件 外, 都比规格值 120 低不少, 反倒认为可以通过. 这是为什么?

我们说,问题不能这么简单地看.

a. 首先, 我们注意到, 甲厂的 \(S=0.4\) 远低于乙厂的 \(S=\) 6.105 , 这表明, 甲厂产品规格比乙厂稳定得多.

b. 也正因为甲厂产品规格很齐整 (误差很小), 所以, 与标准值 120 的些微差别 (此处 \(\bar{X}=119.5\) 比 120 只差 0.5 ) 也被检出来了. 不能不承认: 甲厂产品的平均规格, 有很大可能略低于标准值 120. 虽只略低些, 也是事实, 不能委之于随机误差. 至于这样一个 差别的实际重要性如何, 那要另当别论了, 此处只讲统计上的显著 性-一即差异不能用随机误差解释. 统计上显著的差异不一定有 现实重要性.

c.乙厂抽出的几件产品的指标大多远低于标准值 120 , 使我 们很有理由怀疑,该厂产品平均规格达不到 120 . 但是, 由于该厂 产品质量波动太大, 所测得的数据尚不能很有把握认为, 其平均规 格确与 120 有差距, 而非随机性影响所致, 就是说, 现有数据可能 太少了些.

所以,对乙厂我们首先认为: 其产品质量波动太大应当改进. 至于其平均规格是否与 120 有差距的问题, 可以再补充一些数据 再检定, 最好是先能采取措施把方差缩小些再决定这个问题.

0.2. 2 两个正态总体均值差的检验

设 \(\mathrm{X}_{1}, \cdots, X_{n}\) 是从正态总体 \(N\left(\theta_{1}, \sigma^{2}\right)\) 中抽出的样本, \(Y_{1}\), \(\cdots, Y_{m}\) 是从正态总体 \(N\left(\theta_{2}, \sigma^{2}\right)\) 中抽出的样本. \(\theta_{1}, \theta_{2}\) 都末知, \(\sigma^{2}\) 可以是已知或末知. 注意两总体有同一方差 \(\sigma^{2}\).

给定常数 \(\theta_{0}\), 所要考虑的检验问题是:

\[ \begin{array}{ll} 1^{\circ} & H_{0}: \theta_{1}-\theta_{2} \geqslant \theta_{0}, H_{1}: \theta_{1}-\theta_{2}<\theta_{0} \\ 2^{\circ} & H_{0}^{\prime}: \theta_{1}-\theta_{2} \leqslant \theta_{0}, H_{1}: \theta_{1}-\theta_{2}>\theta_{0} \\ 3^{\circ} & H_{0}^{\prime \prime}: \theta_{1}-\theta_{2}=\theta_{0}, H^{\prime \prime}{ }_{1}: \theta_{1}-\theta_{2} \neq \theta_{0} \end{array} \]

在应用上常见的情况是 \(\sigma^{2}\) 末知，而 \(\theta_{0}=0\).

所有概念上的讨论与前一段没有本质差异. 先说 \(\sigma^{2}\) 已知的情 形. 以 \(\bar{X}\) 和 \(\bar{Y}\) 分别记 \(X\) 样本和 \(Y\) 样本的均值, 则 \(\bar{X}-\bar{Y}\) 为 \(\theta_{1}-\theta_{2}\) 的估计. 于是对问题 \(1^{\circ}\) 而言, 一个合适的检验是当 \(\bar{X}-\bar{Y} \geqslant C\) 时 接受 \(H_{0}\), 不然就否定 \(H_{0}\). 如何根据给定的检验水平 \(\alpha\) 去决定常数 \(C\), 其过程与决定检验 (2.1) 中的 \(C\) 而得到 (2.3) 一样. 所不闰的 是: 这里 \(\bar{X}-\bar{Y}\) 的方差是 \((1 / n+1 / m) \sigma^{2}\), 因而相应地, \((2.3)\) 式中 的 \(\sqrt{n}\) 要改为 \(\sqrt{n m /(n+m)}\). 这样得到 \(C=\theta_{0}-\sigma u_{a}\) \(\sqrt{(n+m) / n m}\). 如果引进统计量

\[ U=\sqrt{\frac{n m}{n+m}}\left(\bar{X}-\bar{Y}-\theta_{0}\right) / \sigma \]

则 1 “的一个水平 \(\alpha\) 检验为

\[ g \text { : 当 } U \geqslant-u_{\alpha} \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

类似地,问题 \(2^{\circ}, 3^{\circ}\) 的水平 \(\alpha\) 检验为

\[ \begin{gathered} g^{\prime} \text { : 当 } U \leqslant u_{\alpha} \text { 时接受 } H_{0}^{\prime} \text {, 不然就否定 } H_{0}^{\prime} \\ g^{\prime \prime} \text { : 当 }|U| \leqslant u_{\alpha / 2} \text { 时接受 } H_{0}^{\prime \prime} \text {, 不然就否定 } H_{0}^{\prime \prime} \end{gathered} \]

对 \(\sigma^{2}\) 末知的情况, 处理也与前一段一样, 即通过样本对之进行估 计, 以估计值代替 \(\sigma^{2}\). 这里有两组样本可用于估计 \(\sigma^{2}\), 将其综合, 得出较好的估计值

\[ S^{2}=\frac{1}{n+m-2}\left(\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}+\sum_{j=1}^{m}\left(Y_{j}-\bar{Y}\right)^{2}\right) \]

以 \(S\) 代替 \(U\) 中的 \(\sigma\), 得检验统计量

\[ T=\sqrt{\frac{n m}{n+m}}\left(\bar{X}-\bar{Y}-\theta_{0}\right) / S \]

按第 膏 (4.36) 式, 当 \(\theta_{1}-\theta_{2}=\theta_{0}\) 时, \(T\) 服从自由度为 \(n+m-2\) 的 \(t\) 分隹 \(t_{n+m}\). 基于 \(T\), 作出在 \(\sigma^{2}\) 末知时, 检验问题 \(1^{\circ}-3^{\circ}\) 的 水平 \(\alpha\) 检验 \(h, h^{\prime}\) 和 \(h^{\prime \prime}\), 分别为

\(h:\) 年 \(T \geqslant-t_{n+m}(\alpha)\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\)

\(h^{\prime}\) : 奖 \(T \leqslant t_{n+m}(\alpha)\) 时接受 \(H_{0}^{\prime}\), 不然就否定 \(H_{0}^{\prime}\)

\(h^{\prime \prime}\) : 当 \(|T| \leqslant t_{n+\ldots-2}(\alpha / 2)\) 时接受 \(H_{0}^{\prime \prime}\), 不然就否定 \(H_{0}^{\prime \prime}\)

这二个检验 \(h, h^{\prime}, h^{\prime \prime}\) ”都称为 “两样本 \(t\) 检验”, \(h\) 和 \(h^{\prime}\) 是单侧 的而 \(h\) ”是双侧的. 它们都属于应用上重要的检验. 问题提法中有 一个不大自然的条件一两总体有同一方差, 不作这一假定就无 法使用 \(t\) 分布. 这是一个为了迁就数学上的简单化而对实用背景 有所损失的例子. 所幸的是: 只要两总体方差之比与 1 相差不太 大,则经验表明,使用 \(t\) 检验是可以令人满意的.

例 2.2 甲、乙两厂生产同一种产: 品, 其质量指标假定分别服 从正态分布 \(N\left(\theta_{1}, \sigma^{2}\right)\) 和 \(N\left(\theta_{2}, \sigma^{2}\right)\). 现从该两厂分别抽出若干件 产品测得其指标值:

\[ \begin{aligned} & \text { 甲厂: } 2.74,2.75,2.72,2.69\left(X_{1}, \cdots, X_{4}\right) \\ & \text { 乙厂: } 2.75,2.78,2.74,2.76,2.72\left(Y_{1}, \cdots, Y_{5}\right) \end{aligned} \]

要通过这些数据来检验这两厂产品质量何者为优.

在这种问题中, 你可以用估计的方法去处理: 甲厂样本平均 \(\bar{X}=2.725\), 乙厂样本平均 \(\bar{Y}=2.75\), 因 \(\bar{Y}>\bar{X}\), 从所抽样本看乙5 较优. 但这还不甚令人信服, 因为这个差距也可以是因为抽样的随 机性而来, 不一定反映本质。

也可以用区间估计的方法来处理这个问题, 算出 \(\bar{X}-\bar{Y}=\) -0.025 ,

\[ \begin{aligned} S^{2} & =\left[\sum_{i=1}^{+}\left(X_{i}-\bar{X}\right)^{2}+\sum_{j=1}^{5}\left(Y_{j}-\bar{Y}\right)^{2}\right] /(4+5-2) \\ & =0.00058571, \quad S=0.0242 \end{aligned} \]

\(n=4, m=5\). 取置信系数 0.95 , 查表得 \(t_{7}(0.025)=2.365\). 用第四 章(4.6)式得 \(\theta_{1}-\theta_{2}\) 的区间估计为

\[ -0.025 \pm 0.0242 \times 2.365 \sqrt{9 / 20}=[-0.063,0.013] \]

这个区间既包含大于 0 的值也包含小于 0 的值, 表示 \(\theta_{1}>\theta_{2}, \theta_{1}=\) \(\theta_{2}\) 和 \(\theta_{1}<\theta_{2} 三\) 种情况都有可能. 区间整个偏向于负轴一边, 显示 情况略有利于乙厂. 但最大差距也只达到 0.063 . 如果这么大小的 差距并无实际重要性, 则可以说, 区间佔计的结果显示了两厂产品 的质量水平大体相当.

如果要用假设检验来处理这个问题,则晴果取决于原假设的 提法, 而这要参考问题的背景.例如, 若以往的记录表明: 甲厂产品 质量一般或经常优于乙厂, 现在我们想通过实测检验一下目前情 况如何. 这时, 我们取 \(H_{0}: \theta_{1}-\theta_{2} \geqslant 0\) 为原假设. 这个取法, 配之以 较低的检验水平, 保证了必须有很强的证据才能否定 \(H_{0}\) 一即改 变对现状的看法. 这是因为, 这个现状, 即 \(H_{0}\), 已经历了一段时期 的考验, 除非实测结果表现出很不利于它, 人们还是倾问于把数据 中表现出来的不利于它的差异委之于随机性.

按 \(\theta_{0}=0, \bar{X}-\bar{Y}=-0.025, S=0.024\), 算出 (2.19)式的统计 量 \(T\) 之值为 -1.540 . 查表得 \(t_{7}(0.05)=1.895\). 因为 \(-1.540>\) -1.895 , 按 \(t\) 检验, 应接受 \(H_{0}\), 即维持“甲厂严品质量优于乙厂” 的看法. 或者说, 实测数据没有提供改变这个看法的有力证据.

如果我们一开始就采用 \(H_{0}^{\prime}: \theta_{1}-\theta_{2} \leqslant 0\) 作为原假设,则所得 数据当然也使它通过. 这种表面上的矛盾已在前面解释过了.

如果我们不涉及以往两厂产品质量上的表现, 而单纯以 “中 立” 的态度来对待这个比较问题, 则合适的原假设是 \(H_{0}^{\prime \prime}: \theta_{1}-\theta_{2}\) \(=0\), 用所得数据检验的结果, 仍接受 \(H_{0}\). 这个结论也与我们上文 的分析一致.

我们把上面的问题的提法作一点变化,借此解释一下显著性 和显著性检验这两个概念.

一工厂用一定工艺生产某种产品有相当时间. 现有人提出对 工艺作些更改以图改进产品质量. 设在工艺改变前后产品质量指 标的分布分别为 \(N\left(\theta_{1}, \sigma^{2}\right)\) 和 \(N\left(\theta_{2}, \sigma^{2}\right)\). 如果 \(\theta_{2}>\theta_{1}\), 就表示产 品质量确有改进. 现要通过试验来决定此项工艺改变是否可取. 为 此, 抽取工艺改变前后的产品各若干个以测定其质量. 以 \(X_{1}, \cdots\), \(X_{n}\) 和 \(Y_{1}, \cdots, Y_{m}\) 分别记工艺改变前后的抽样测定数据.

即便不从统计学方法的角度去考虑, 人们也多半会采用如下 的判据: 计算 \(\bar{Y}-\bar{X}\), 只有当 \(\bar{Y}-\bar{X}\) 达到或超过某个界限 \(C\) 时, 才 认为工艺改变后产品质量有“显著”提高因而值得采用. 这个界限 \(C\) 可以通过改变工艺所需费用与所得收益的分析去确定,但这种 不涉及统计方法的分析有一点不足之处, 即它没有考虑随机误差 的影响. 采用假设检验的观点去分析这个问题, 是克服这一不足之 处的一个方法.

按假设检验的观点, 我们应当把 \(H_{0}: \theta_{1} \geqslant \theta_{2}\) 取为原假设. 如 以前多次讲过的, 这个取法, 辅之以较低的检验水平 \(\alpha\), 保证了它 不会轻易被否定, 必须有很强的证据才能使我们接受“工艺改变确 能提高产品质量”的看法. 按检验 \(h\) (见 (2.20)), 这只有在

\[ \bar{Y}-\bar{X}>S t_{n+m-2}(\alpha) \sqrt{(n+m) / n m} \]

时成立.

当这种情况出现时一也就是说, 原假设 \(\theta_{1} \geqslant \theta_{2}\) 在水平 \(\alpha\) 上 被否定时,我们说 \(\bar{Y}-\bar{X}\) 达到了“显著性”, 即差异如此显著, 以至 可以否定 \(\theta_{1} \geqslant \theta_{2}\). 以此之故,这一检验也就称为“业著性检验”.

从统计学的观点看, 达到显著性无非是指: 在给定水平上, 差 异 \((\bar{Y}-\bar{X})\) 已不能仅由随机性来解释, 而也有 \(\theta_{2} \geqslant \theta_{1}\) 的原因. 统 计上的显著性不一定意味着 \(\bar{Y}-\bar{X}\) 很大. 实际上, 由 (2.23) 看出: 若 \(n, m\) 很大, 或 \(S\) 很小, 则 \(\bar{Y}-\bar{X}\) 只须略大于 0 就可以达到鼠 著性. 由此可见, 是否达到显著性并非应否采取某种行动(在此为 修改工艺)的唯一依据, 还须结合其他方面的考虑, 如前面所曾提 到的.

从某种意义上说,任何一个检验都可以理解为显著性检验.但 显著性检验这个名词最常用于有关某种效应或差异是否存在的那 种问题，且我们主观上是希望该效应存在的.如在本例中,我们自 然希望,工艺的修改确有助于产品质量的提高. 这与例 2.2 那种种 情况选择原假设时所依据的考虑不同，在这种情况，我们有理由倾 向于相信原假设成立.

所以,你可以简单地把“显著性检验”理解为“希望原假设被否 定的那种检验”. 显著性检验的特点不在于这检验自身, 而在于其 在使用中的含义如何.

0.3. 3 正态分布方差的检验

包括一个正态分布方差的检验和两个正态分布的方差之比的 检验. 和正态分布均值的检验相比, 方差的检验在应用上较少一 些,但也有一些应用.例如，一种仪器或一种测定方法的精度 (指其 内在误差, 不是指由于没有调准而产生的偏离) 是否达到某种界 限,当一种产品的质量问题主要在于波动太大时,可能需要检验方 差; 方差比检验可用于检验两个方差相等的假定（如在两样本 \(t\) 检 验中) 是否合理等.

先考虑一个正态总体的情况. 设 \(X_{1}, \cdots, X_{n}\) 是从正态总体 \(N\) \(\left(\theta, \sigma^{2}\right)\) 中抽出的样本. \(\sigma^{2}\) 末知, \(\theta\) 可以已知或末知. 以下只讨论 \(\theta\) 末知的情况 ( \(\theta\) 已知的情况读者自己给出). 设 \(\sigma_{0}^{2}\) 为给定的数. 可 以提出以下几个检验问题:

\(1^{\circ} \quad H_{0}: \sigma^{2} \geqslant \sigma_{0}^{2}, H_{1}: \sigma^{2}<\sigma_{0}^{2}\)

\(2^{\circ} \quad H_{0}^{\prime}: \sigma^{2} \leqslant \sigma_{0}^{2}, H_{1}^{\prime}: \sigma^{2}>\sigma_{0}^{2}\)

\(3^{\circ} \quad H_{0}^{\prime \prime}: \sigma^{2}=\sigma_{0}^{2}, H_{1}^{\prime \prime}: \sigma^{2} \neq \sigma_{0}^{2}\)

先考虑 \(1^{\circ}\). 取 \(\sigma^{2}\) 的估计 \(S^{2}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} /(n-1) .1^{\circ}\) 的… 个直观上合理的检验为

\[ \varphi \text { : 当 } \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} \geqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

为定出 \(C\), 要计算 \(\varphi\) 的功效函数. 以 \(K_{n-1}(x)\) 记自由度为 \(n-1\) 的卡方分布函数,则按第二章 \((4.33)\), 有

\[ \begin{aligned} \beta_{\varphi}(\theta, \sigma) & =P_{\theta, \sigma}\left(\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}<C\right) \\ & =P_{\theta, \sigma}\left(\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} / \sigma^{2}<C / \sigma^{2}\right) \\ & =K_{n-1}\left(C / \sigma^{2}\right) \end{aligned} \]

注意 \(\beta_{\varphi}(\theta, \sigma)\) 与均值 \(\theta\) 无关, 且为 \(\sigma^{2}\) 的下降函数. 故只须找 \(C\), 使 \(K_{n-1}\left(C / \sigma_{0}^{2}\right)=\alpha\). 这得出

\[ C=\sigma_{0}^{2} \chi_{n-1}^{2}(1-\alpha) \]

(2.24) 和 (2.26) 结合定出了问题 \(1^{\circ}\) 的检验 \(\varphi\). 类似地, 得出问题 \(2^{\circ}\) 的检验 \(\varphi^{\prime}\) 和问题 \(3^{\circ}\) 的检验 \(\varphi^{\prime \prime}\), 分别为

\[ \begin{gathered} \varphi^{\prime} \text { : 当 } \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} \leqslant \sigma_{0}^{2} \chi_{n-1}^{2}(\alpha) \text { 时接受 } H_{0}^{\prime} \text {, 不然就否定 } H_{0}^{\prime} \\ \varphi^{\prime \prime} \text { : 当 } \sigma_{0}^{2} \chi_{n-1}^{2}\left(1-\frac{\alpha}{2}\right) \leqslant \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2} \leqslant \sigma_{0}^{2} \chi_{n-1}^{2}\left(\frac{\alpha}{2}\right) \text { 时接受 } \\ H_{0}^{\prime \prime} \text {, 不然就否定 } H_{0}^{\prime \prime} \end{gathered} \]

例如, 取样本大小 \(n=30, \alpha=0.05\). 查表得

\[ \begin{aligned} & \chi_{29}^{2}(0.025)=45.722, \chi_{29}^{2}(0.05)=42.557 \\ & \chi_{29}^{2}(0.975)=16.046 \end{aligned} \]

取水平 \(\alpha=0.05\), 检验 \(\varphi^{\prime}\) 要求在

\[ S^{2} \leqslant \sigma_{0}^{2}(42.557) / 29=1.467 \sigma_{0}^{2} \]

时, 接受 \(\sigma^{2} \leqslant \sigma_{0}^{2}\) 之假设. 就是说, 在方差估计值 \(S^{2}\) 大约为 \(\sigma_{0}^{2}\) 的 1.5 倍时, 仍得接受方差 \(\sigma_{0}^{2}\). 如果是双侧检验 \(\varphi^{\prime \prime}\), 则差距更大, 它 要求在

\[ 0.533 \sigma_{0}^{2} \leqslant S^{2} \leqslant 1.577 \sigma_{0}^{2} \]

时接受 \(H_{0}^{\prime \prime}: \sigma^{2}=\sigma_{0}^{2}\). 上述不等式之上界约为下界之三倍，这说明： 直至像 30 这么大小的样本, 方差检验仍甚不可靠 (许多远离 \(\sigma_{0}^{2}\) 之 值仍能被接受为等于 \(\sigma_{0}^{2}\), 即犯第二类错误的概率会甚大).

现考虑两个正态总体的情况, 设 \(X_{1}, \cdots, X_{n}\) 和 \(Y_{1}, \cdots, Y_{m}\) 分 别是从正态总体 \(N\left(\theta_{1}, \sigma_{1}^{2}\right)\) 和 \(N\left(\theta_{2}, \sigma_{2}^{2}\right)\) 中抽出的样本, 可提出以 下几个检验问题:

\[ \begin{array}{ll} 1^{\circ} & H_{0}: \sigma_{1}^{2} / \sigma_{2}^{2} \geqslant a, H_{1}: \sigma_{1}^{2} / \sigma_{2}^{2}<a \\ 2^{\circ} & H_{0}^{\prime}: \sigma_{1}^{2} / \sigma_{2}^{2} \leqslant a, H_{1}^{\prime}: \sigma_{1}^{2} / \sigma_{2}^{2}>a \\ 3^{\circ} & H_{0}^{\prime \prime}: \sigma_{1}^{2} / \sigma_{2}^{2}=a, H_{1}^{\prime \prime}: \sigma_{1}^{2} / \sigma_{2}^{2} \neq a \end{array} \]

\(a\) 为给定的数. 事实上, \(2^{\circ}\) 可转化为 \(1^{\circ}\), 只须掉换 \(\sigma_{1}^{2}\) 和 \(\sigma_{2}^{2}\) 的位置 即可. 故只须考虑 \(1^{\circ}\) 和 \(3^{\circ}\).

考虑 \(1^{\circ}\). 以 \(S_{1}^{2}\) 和 \(S_{2}^{2}\) 分别记 \(X\) 样本和 \(Y\) 样本的样本方差. 则 \(S_{1}^{2} / S_{2}^{2}\) 为 \(\sigma_{1}^{2} / \sigma_{2}^{2}\) 的一个估计值. 故问题 \(1^{\circ}\) 的一个直观上合理的检 验为

\[ \dot{\psi} \text { : 当 } S_{1}^{2} / S_{2}^{2} \geqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

其功效函数为

\[ \begin{aligned} \beta_{\psi}\left(\theta_{1}, \theta_{2}, \sigma_{1}, \sigma_{2}\right) & =P_{\theta_{1}, \theta_{2}, \sigma_{1}, \sigma_{2}}\left(S_{1}^{2} / S_{2}^{2}<C\right) \\ & =P_{\theta_{1}, \theta_{2}, \sigma_{1}, \sigma_{2}}\left(\frac{1}{\sigma_{1}^{2}} S_{1}^{2} / \frac{1}{\sigma_{2}^{2}} S_{2}^{2}<\frac{\sigma_{2}^{2}}{\sigma_{1}^{2}} C\right) \\ & =G_{n-1, m-1}\left(\sigma_{2}^{2} C / \sigma_{1}^{2}\right) \end{aligned} \]

此处 \(G_{n-1, m-1}(x)\) 是自由度为 \((n-1, m-1)\) 的 \(F\) 分布函数（见 第二章 \((4.35))\). 此函数是 \(\sigma_{1}^{2} / \sigma_{2}^{2}\) 的下降函数. 故只须决定 \(C\), 使 \(G_{n-1, m-1}(C / a)=\alpha\) 即可. 由此得

\[ C=a F_{n-1, m-1}(1-a)=a / F_{m-1, n-1}(\alpha) \]

最后一式见第二章习题.

类似地导出检验问题 \(3^{\circ}\) 的一个检验为: 当 \(C_{1} \leqslant S_{1}^{2} / S_{2}^{2} \leqslant C_{2}\) 时接受原假设 \(H_{0}^{\prime \prime}\), 不然就否定 \(H_{0}^{\prime \prime}\), 其中

\[ C_{1}=a / F_{m-1, n-1}(\alpha / 2), C_{2}=a F_{n-1, m-1}(\alpha / 2) \]

\(\alpha\) 为检验的水平.

1. 2 .4 指数分布参数的检验

指数分布的密度函数是第二章 \((1.20)\) 式,分布函数则是该章 (1.21) 式. 它是一个单参数分布族一一只包含一个参数 \(\lambda\). 这个分 布的重要性在于: 如我们曾指出的, 它描述了在一定条件下元件等 的寿命分布, 因此在可靠性分析中是- - 个基础性的分布, 有不少的 应用。

现设 \(X_{1}, \cdots, X_{n}\) 是从这总体中抽出的样本. 在实际应用中, 这 可以是 \(n\) 个抽来供试验的元件, 从开始试验起到失效为止,各元 件经历的时间, 要根据这些数据检验以下这些假设 \(\left(\lambda_{0}\right.\) 给定):

\[ \begin{array}{ll} 1^{\circ} & H_{0}: \lambda \geqslant \lambda_{0}, H_{1}: \lambda<\lambda_{0} \\ 2^{\circ} & H_{0}^{\prime}: \lambda \leqslant \lambda_{0}, H_{1}^{\prime}: \lambda>\lambda_{0} \\ 3^{\circ} & H_{0}^{\prime \prime}: \lambda=\lambda_{0}, H_{1}^{\prime \prime}: \lambda \neq \lambda_{0} \end{array} \]

我们已经知道: \(\bar{X}\) 是 \(1 / \lambda\) 的无偏估计. 当 \(H_{0}\) 成立时, \(\bar{X}\) 应倾 向于取较小的值. 于是, 问题 \(1^{\circ}\) 的一个直观上合理的检验为

\[ \psi \text { : 当 } \widetilde{X} \leqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

这个检验的功效函数不难计算. 因为当参数值为 \(\lambda\) 时, 有

\[ 2 \lambda\left(X_{1}+\cdots+X_{n}\right)=2 n \lambda \bar{X}-\chi^{\frac{2}{2} n} . \]

因此

\[ \begin{aligned} \beta_{\varphi}(\lambda) & =P_{\lambda}(\bar{X}>C)=P_{\lambda}(2 n \lambda \bar{X}>2 n \lambda C) \\ & =1-K_{2 n}(2 n \lambda C) \end{aligned} \]

这里 \(K_{2 n}(x)\) 是 \(\chi^{\frac{2}{2} n}\) 的分布函数, \(\beta_{\varphi}(\lambda)\) 为 \(\lambda\) 的下降函数,故为使 检验 \(\varphi\) 有指定的水平 \(\alpha\), 只须取 \(C\), 使

\[ \beta_{\varphi}\left(\lambda_{0}\right)=1-K_{2 n}\left(2 n \lambda_{0} C\right)=\alpha \]

这导致 \(2 n \lambda_{0} C=\chi^{\frac{2}{2} n}(\alpha)\) ，而

\[ C=\chi_{2 n}^{2}(\alpha) /\left(2 n \lambda_{0}\right) \]

若指定 \(\lambda_{1}<\lambda_{0}\), 而要求当 \(\lambda \leqslant \lambda_{1}\) 时，接受原假设 \(H_{0}\) 的概率 不超过给定的相当小的数 \(\beta\), 则由 \(\beta_{\varphi}(\lambda)\) 为 \(\lambda\) 的下降函数,知只须 有 \(\beta_{\varphi}\left(\lambda_{1}\right)=1-\beta\), 即

\[ K_{2 n}\left(\chi^{\frac{2}{2} n}(\alpha) \lambda_{1} / \lambda_{0}\right)=\beta \]

利用此式可用试算法结合查 \(\chi^{2}\) 分布表去决定 \(n\). 先取一个试探性 的 \(n\) 代人上式左边. 若讨算结果小于 \(\beta\), 则 \(n\) 取得太大. 若大于 \(\beta\), 则 \(n\) 取得太小. 经过调整 \(n\) 之值后再算. 类似地可得到检验问题 \(2^{\circ}\) 和 \(3^{\circ}\) 的水平 \(\alpha\) 检验 \(\varphi^{\prime}\) 和 \(\varphi^{\prime \prime}\) : \(\varphi^{\prime}\) : 当 \(\bar{X} \geqslant \chi_{2 n}^{2}(1-\alpha) /\left(2 n \lambda_{0}\right)\) 时接受 \(H_{0}^{\prime}\), 不然就否定 \(H_{0}^{\prime}\)

\[ \begin{gathered} \varphi^{\prime \prime} \text { : 当 } \chi^{\frac{2}{2} n}\left(1-\frac{\alpha}{2}\right) /\left(2 n \lambda_{0}\right) \leqslant \bar{X} \leqslant \chi_{2 n}^{2}\left(\frac{\alpha}{2}\right) /\left(2 n \lambda_{0}\right) \text { 时接受 } \\ H_{0}^{\prime \prime} \text {, 不然就否定 } H_{0}^{\prime \prime} \end{gathered} \]

可以证明 (见附录 \(A\) ) : \(\varphi\) 和 \(\varphi^{\prime}\) 都是相应假设的一致最优检验, 而 \(\varphi^{\prime \prime}\) 则不是一问题 \(3^{\circ}\) 没有一致最优检验.

我们来看看问题 \(2^{\circ}\). 假设 \(H_{0}^{\prime}\) 可写为

\[ H_{0}^{\prime} \text { : 元件平均寿命 } \geqslant 1 / \lambda_{0} \]

而检验 \(\varphi^{\prime}\) 可写为: “当 \((1 / \bar{X}) /\left(1 / \lambda_{0}\right) \geqslant \chi_{1 n}^{2}(1-\alpha) / 2 n\) 时, 接受 \(H_{0}^{\prime}\) ”. 这意思是说: 只要观察的平均寿命 \(1 / \bar{X}\) 不小于设定的平均 寿命 \(1 / \lambda_{0}\) 的 \(\chi^{\frac{2}{2} n}(1-\alpha) / 2 n\) 倍, 假设 \(H_{0}^{\prime}\) 就可以接受. 取 \(\alpha=\) \(0.05, n=15\), 查表得

\[ \chi^{\frac{2}{2} n}(1-\alpha) / 2 n=\chi_{30}^{2}(0.95) / 30=18.493 / 30=0.6184 \]

即, 只要观察到的平均寿命能达到设定值的约 \(62 \%\), 就可接受 “平 均寿命不小于 \(1 / \lambda_{0}\) ” 的假设. 这看来不大能为人接受, 其解释是： 一则我们选择了较小的水平 \(\alpha\) (要求不轻易否定 \(H_{0}\) ), 一则样本大 小 15 太小了些. 对前者, 若将 \(\alpha\) 上升为 0.3 , 则相应的界限约为 1 / \(\lambda_{0}\) 的 \(85 \%\). 对后者, 若仍维持 \(\alpha=0.05\), 但取 \(n=100\), 将得出相应 的界限约为 \(1 / \lambda_{0}\) 的 \(84 \%\),这已算比较合理了.

因此,在解释假设检验的结果时, 切不能单纯只注意到是接受 还是否定. 接受是在什么条件下, 否定又是在什么情况下, 其含义 如何, 有哪些因素起作用, 都须进行估量, 这样才能得出切合实际 的看法.

2. 截尾寿命检验

直接将前述检验用于元件寿命检验, 在实施上有一个不便之 处: 拿 \(n\) 个元件同时开始使用, 到其全部失效时试验才能停住. 这 \(n\) 个元件中难免有少数几个寿命特长的. 这么一来, 就必须等待很 长的时间才能结束试验, 为免除这个不便, 在实际工作中常采用所 谓截尾法.下面我们把这个方法的实施步骤介绍一下, 其中涉及的 分布问题就不能在此细讲了.

1. 定数截尾法

取 \(n\) 个元件做试验. 定下一个自然数 \(r<n\), 试验进行到有 \(r\) 个元件失效时为止. 把到此时为止, 全部 \(n\) 个元件的工作时间加 起来记为 \(T\), 即

\[ T=Y_{1}+\cdots+Y_{r}+(n-r) Y_{r} \]

这里 \(Y_{1}\) 是最先失效的那个元件的失效时刻 (从时刻 0 开始算 起), \(Y_{2}\) 为第二失效的元件的失效时刻. 以此类推,第 \(r\) 个失效元 件在时刻 \(Y_{r}\), 试验也就到此为止, 余下尚有 \(n-r\) 个末失效元件, 它们已工作的总时间为 \((n-r) Y_{r}\). 这样得到 \(T\) 的表达式(2.34). 不难理解: \(T\) 愈大, 就愈使我们相信元件的平均寿命大. 因此, 比 如说, 问题 \(2^{\circ}\) 的一个合理检验为

\(\psi\) : 当 \(T \geqslant C\) 时接受原假设 \(H_{0}^{\prime}\), 不然就否定 \(H_{0}^{\prime}\) (2.35) 可以证明 * : 当参数值为 \(\lambda\) 时, \(2 \lambda T \sim \chi^{2} r\). 由此出发, 仿前面的推 理, 就不难在给定检验水平 \(\alpha\) 之下定出 (2.35) 中的 \(C\) 为

\[ C=\chi^{\frac{2}{2}}(1-\alpha) /\left(2 \lambda_{0}\right) \]

例如, 要检验某种元件平均寿命不小于 5000 小时这个原假 设. 这相当于问题 \(2^{\circ}\), 并且 \(\lambda_{0}=1 / 5000\). 取 15 个元件做试验, 预定 到第 5 个失效时, 试验停止. 于是 \(n=15, r=5\). 设前 5 个失效元件 的工作时间依次是

\[ 800,1200,1500,2000,2200 \text { (小时) } \]

则 \(T=800+1200+1500+2000+2200+10 \times 2200=27500 \alpha=\) 0.05 , 查表得

\[ C=\chi_{10}^{2}(0.95) \times 2500=3.940 \times 2500=9850 \]

因为 \(27500>9850\), 应接受原假设 \(\lambda \leqslant 1 / 5000\).

• 见本章习题 15

3. 2. 定时截尾法

指定一个时刻 \(T_{0}\), 拿 \(n\) 个元件做试验, 直到时刻 \(T_{0}\) 为止. 把 到这时为止全部 \(n\) 个元件的工作总时间加起来记为 \(T^{*}\), 算法是： 若某个元件在 \(T_{0}\) 之前的某个时刻 \(t\) 已失效,则该元件的工作时 间为 \(t\). 若到 \(T_{0}\) 时刻仍末失效, 则该元件的工作时间为 \(T_{0} \cdot{ }^{*}\) 显 然, 平均寿命愈大, 则 \(T^{*}\) 愈倾向于取较大之值, 于是得出检验：

\[ \dot{\psi}^{\prime} \text { : 当 } T^{*} \geqslant C \text { 时接受 } H_{0}^{\prime} \text {, 不然就否定 } H_{0}^{\prime} \]

可以证明: 近似地有 \(2 \lambda T^{*} \sim \chi_{2}^{2} u+1\). 这里 \(u\) 是到时刻 \(T_{0}\) 停试时已 失效的元件个数. 由此出发,仿前面的推理,即可定出在给定水平 \(\alpha\) 时 \(C\) 的近似值 (因 \(2 \lambda T^{*}-\chi_{2: 4+1}^{2}\) 只是近似成立), 为

\[ C=\chi_{2 u+1}^{2}(1-\alpha) /\left(2 \lambda_{0}\right) \]

例如，仍取 \(\lambda_{0}=1 / 5000, \alpha=0.05\), 取 10 个元件做试验,把 \(T_{0}\) 定为 1000 . 到时刻 \(T_{0}\) 时, 已有 5 个元件失效, 时刻分别为 100 , \(150,230,500\) 和 580 , 则

\[ T^{*}=100+150+230+500+580+5 \times 1000=6560 \]

此处 \(u=5\), 按 \((2.37)\), 有

\[ C=\chi_{11}^{2}(0.95) \times 2500=4.575 \times 2500=11437.5 \]

因为 \(6560<11437.5\), 应否定原假设 \(H_{0}^{\prime}\).

3.1. 5 二项分布参数 \(p\) 的检验

设某事件的概率为 \(p, p\) 末知. 作 \(n\) 次独立试验,每次观察该 事件是否发生. 以 \(X\) 记该事件发生的次数, 则 \(X\) 服从二项分布 \(B\) \((n, p)\). 要根据 \(X\) 去检验以下一些假设：

\(1^{\circ} H_{0}: p \leqslant p_{0}, H_{1}: p>p_{0}\)

\(2^{\circ} \quad H_{0}^{\prime}: p \geqslant p_{0}, H_{1}^{\prime}: p<p_{0}\)

\(3^{\circ} \quad H_{0}^{\prime \prime}: p=p_{0}, H_{1}^{\prime \prime}: p \neq p_{0}\)

• 也可以更一般一些, 对参试的 \(n\) 个元件的每一个规定不同的停试时刻 \(T_{1}, \cdots\), \(T_{n}\) ，总工作时间 \(T\) 计算方法与上述相同 先考虑 \(1^{\circ}\). 从直观上看, 一个显然的检验法为

\[ \varphi \text { : 当 } X \leqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

因 \(X\) 只取整数值, 故 \(C\) 可限于整数. 此检验的功效函数为

\[ \begin{aligned} \beta_{\varphi}(p) & =P_{p}(X>C)=1-P_{p}(X \leqslant C) \\ & =1-\sum_{i=0}^{c}\left(\begin{array}{l} n \\ i \end{array}\right) p^{i}(1-p)^{n-i} \end{aligned} \]

据第二章习题 \(7, \beta_{\varphi}(p)\) 为 \(p\) 的增函数. 故只须取 \(C\), 使 \(\beta_{\varphi}\left(p_{0}\right)=\) \(\alpha\), 则检验 \(\varphi\) 将有水平 \(\alpha\). 这相当于要选择整数 \(C\), 使

\[ \sum_{i=0}^{c}\left(\begin{array}{l} n \\ i \end{array}\right) p_{0}^{i}\left(1-p_{0}\right)^{n-i}=1-\alpha \]

麻烦的是, 不一定正好有一个整数 \(C\) 使 (2.40) 成立. 较常见的情 况是: 存在这样一个 \(C_{0}\). 使

\[ \sum_{i=0}^{c_{0}}\left(\begin{array}{l} n \\ i \end{array}\right) p_{0}^{i}\left(1-p_{0}\right)^{n-i}<1-\alpha<\sum_{i=0}^{c_{0}+1}\left(\begin{array}{l} n \\ i \end{array}\right) p_{0}^{i}\left(1-p_{0}\right)^{n-i} \]

这时, 我们只好 取 \(C\) 为 \(C_{0}\) 或 \(C_{0}+1\). 当取 \(C\) 为 \(C_{0}\) 时, 相当于把 水平 \(\alpha\) 升高一些, 即允许犯第一类错误的概率略大一点. 当取 \(C\) 为 \(C_{0}+1\) 时,则相当于把水平 \(\alpha\) 降一点,只要 \(n\) 充分大,则

\[ \left(\begin{array}{c} n \\ C_{0}+1 \end{array}\right) p_{0}^{C_{0}+1}\left(1-p_{0}\right)^{n-C_{0}-1} \]

这一项一般很小, 这种修改也就很小, 不会太影响实际. 因为水平 \(\alpha\) 取为 0.05 或 0.01 等并无特殊含义,这样的修改也不产生原则 问题.

但是, 在 \(n\) 不很大时, 有可能 (2.41) 的左右两边都与 \(1-\alpha\) 有 不可忽略的距离, 这时如屈从一端, 则对水平 \(\alpha\) 的修改太大, 可能 对当事的一方不利.举例如下:

例 2.3 一工厂向商店供货, 商店要求废品率不超过 \(p=\) 0.05 . 经双方同意制定抽样方案: 每批 (假定批量很大) 抽 \(n=24\) 件,检查其中废品个数 \(X\), 当 \(X \leqslant C\) 时,商店接受该批产品,否则 就拒收. 双方约定检验水平为 \(\alpha=0.05\), 这意味着废品率为 0.05 的批, 有 \(95 \%\) 可通过检查 (若 \(p<0.05\), 通过的比率当然比 0.95 更高). 问题是决定 \(C\), 按 (2.40), 要找 \(C\) 使

\[ I=\sum_{i=0}^{c}\left(\begin{array}{l} 24 \\ i \end{array}\right)(0.05)^{i}(0.95)^{24-i}=0.95 \]

查二项分布表 \({ }^{*}\),知

\[ C=2 \text { 时, } I=0.884 ; C=3 \text { 时, } I=0.970 \]

此两值都与约定的 0.95 有相当距离. 若取 \(C=2\), 对商店有利; 取 \(C=3\) 则对工厂有利.

照数字看, 0.97 与 0.95 距离较近, 似以把 \(C\) 取为 3 较合理. 但如商店不同意,一定要坚持 0.95 这个数,则只好按如下的方式 处理:

a. 当 \(X \leqslant 2\) 时接受产品 (接受假设 \(p \leqslant 0.05\) ), 当 \(X \geqslant 4\) 时拒收.

b. 若 \(X=3\), 则既不完全接受也不完全拒绝, 而按一定的概率接 受. 接受的概率是

\[ r=(0.95-0.884) /(0.97-0.884)=0.767 \]

可以这样设想: 拿一个袋子, 其中含白球 767 个, 红球 233 个. 每次 抽样得出 \(X=3\) 时, 即随机从袋子中抽出 - 个球, 如为白球, 产品 通过:否则就拒收.

\(\mathrm{a}, \mathrm{b}\) 二者结合就严格维持了 0.05 这个约定的水平. 这样的检 验叫做“随机化检验”, 因为在 \(\mathrm{b}\) 这个步骤中, 包含了一个随机机制 去决定原假设是否被接受. 在所有涉及离散型分布的检验中,如要 坚持约定的水平, 往往得通过这样的随机化. 但这种做法,一则䋆 赘,二则对实用工作者而言往往觉得不自然. 因此,除非确有必要, 实用上不大采用. 这里交代了以后, 以下我们就不再提这个问题.

继续把问题 \(1^{\circ}\) 看成一个产品抽样验收的问题, 在实际使用

• 目前国内较仔细的二项分布表, 以及其他儿种常用统计表,包括正态分存, 统计 三大分布及波哇松分布等的表,是由全国统计方法应用标准化技术委员会制定的国家 标准,统计分布数值表 GB4086. 中, 除规定 \(p_{0}\) 和水平 \(\alpha\) 外, 还要指定一个较 \(p_{0}\) 大一些的数 \(p_{1}\) 及 充分小的数 \(\beta\), 并要求检验能满足如下的条件: 若 \(p \geqslant p_{1}\), 则原假 设 \(H_{0}\) 被接受的概率不超过 \(\beta\). 就是说, 废品率不小于 \(p_{1}\) 的批, 只 有至多 \(100 \beta \%\) 的批能通过检验. 在抽样验收中,一般使用 \(1-\beta_{\varphi}\) \((p)\) 而不使用 \(\beta_{\varphi}(p) .1-\beta_{\varphi}(p)\) 称为检验 \(\varphi\) 的操作特征函数或 \(O C\) 函数, 暂记为 \(L_{\varphi}(p)\). 有

\[ L_{\varphi}(p)=\sum_{i=0}^{c}\left(\begin{array}{l} n \\ i \end{array}\right) p^{i}(1-p)^{n-i} \]

于是所提的要求可综合为

\[ L_{\varphi}\left(p_{0}\right)=1-\alpha, L_{\varphi}\left(p_{1}\right)=\beta \]

如图 5.3 所示, 为实现 (2.43), 可能试着选一 个 \(n\), 按 \((2.40)\) 决定 \(C\). 定出 \(C\) 后, 把 \(p=p_{1}\) 代人 (2.42) 算出 \(L_{\varphi}\left(p_{1}\right)\). 若 \(L_{\varphi}\left(p_{1}\right)<\beta\), 则 \(n\) 取得太大了. 若 \(L_{\varphi}\left(p_{1}\right)>\beta\), 则 \(n\) 取得太 小,经调整 \(n\) 值之后再重复上述试算。应用 上,对一些特定的 \(p_{0}, p_{1}\) 和 \(\alpha, \beta\) 值,把 \(n\) 和 \(C\) 的值造了表.

产品抽样验收是二项分布参数问题的一

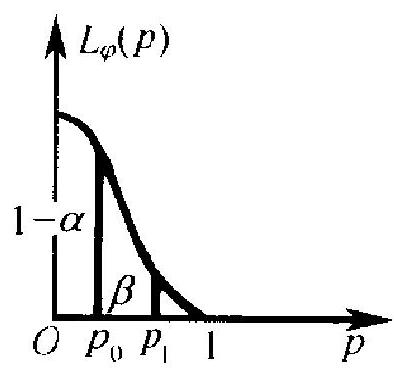
图 5.3 项重要应用, 它已经发展成为数理统计学的一个应用分支, 刚才所 讲只是一种最简单的情况. 实际应用中, 为了对付各种情况一例 如, 每批产品个数不大, 而需要用超几何分布代替二项分布; - 次 完成抽样可能不经济, 而可以考虑多次完成, 如复式抽样方案 (见 习题)及序贯抽样方案; 产品也可以不单纯只看其是否合格, 而要 测定其指标值 (数量验收方案); 验收可以是针对孤立的一些批,或 是连续性的,因而可以考虑在何时放宽或加严检查,等等.

检验问题 \(2^{\circ}, 3^{\circ}\) 的处理方法类似. 给定水平 \(\alpha\), 其检验分别为

\[ \varphi^{\prime} \text { : 当 } X \geqslant C \text { 时接受 } H_{0}^{\prime} \text {, 不然就否定 } H_{0}^{\prime} \]

其中 \(C\) 由关系式

\[ \sum_{i=0}^{C-1}\left(\begin{array}{l} n \\ i \end{array}\right) p_{0}^{i}\left(1-p_{0}\right)^{n-i}=\alpha \]

确定.

\[ \varphi^{\prime \prime} \text { : 当 } C_{1} \leqslant X \leqslant C_{2} \text { 时接受 } H_{0}^{\prime \prime} \text {, 不然就否定 } H_{0}^{\prime \prime}(2.45) \]

其中 \(C_{1}, C_{2}\) 分别由关系式

\[ \left.\begin{array}{l} \sum_{i=0}^{c_{1}-1}\left(\begin{array}{l} n \\ i \end{array}\right) p_{0}^{i}\left(1-p_{0}\right)^{n-i}=\alpha / 2 \\ \sum_{i=c_{2}+1}^{n}\left(\begin{array}{l} n \\ i \end{array}\right) p_{0}^{i}\left(1-p_{0}\right)^{n-i}=\alpha / 2 \end{array}\right\} \]

确定. 可以证明: \(\varphi\) 和 \(\varphi^{\prime}\) 都是所给水平下的一致最优检验,而问题 \(3^{\circ}\) 没有一致最优检验.

符号检验

符号检验的原始形态如下: 假定有甲、乙两种牌号的同一产品 (例如两种椑酒). 为了解大众的反映如何, 挑选了 \(n\) 个人, 每人给 以甲、乙两牌号的产品各一份, 请他们使用后作出评定,规定: 若你 认为甲优于乙, 则给一个 “+ ” 号; 若认为乙优于甲, 则给一个 “- ” 号.以 \(p\) 记“认为甲比乙优”的人在整个大众 (而不止限于挑出的 这 \(n\) 个人) 中所占比例, 若 \(p=1 / 2\), 则甲、乙两种牌子谁也不占优 势. 为检验是否如此 (检验原假设 \(p=1 / 2\) ), 看这 \(n\) 个人的回答中 正号的个数 \(X . X\) 服从二项分布 \(B(n, p)\). 于是可以使用检验 (2.45), \(C_{1}, C_{2}\) 由 (2.46) 给出, 其中 \(p_{0}=1 / 2\). 若 \(X<C_{1}\), 则判甲 不如乙. 若 \(X>C_{2}\), 则判乙不如甲. 若 \(C_{1} \leqslant X \leqslant C_{2}\), 则认为在水平 \(\alpha\) 上尚不足作出判断一尽管在样本中+、一号个数有差别, 但差 别不够大, 还不能认为它一定不是由抽样的随机性所引起.

更进一步,在有些场合下, 可以要求参试的人打分. 如定下 0-100 分的范围, 可以要求每个参试者对甲、乙两牌号的产品各 给一个分,如下表前两行所示.

对这批数据可以考虑用 \(t\) 检验法: 一是把 \(X_{1}, \cdots, X_{n}\) 和 \(Y_{1}, \cdots, Y_{n}\) 分别看作从正态总体 \(N\left(\theta_{1}, \sigma^{2}\right)\) 和 \(N\left(\theta_{2}, \sigma^{2}\right)\) 中抽出的样本，用两 样本 \(t\) 检验 (2.22) 去检验原假设 \(\theta_{1}=\theta_{2}\). 这个做法的问题在于: 各人品味和打分尺度不同. 品味较高的人也许倾向于把分给得低 一些, 反之则给得高一些.这不仅会破坏正态性, 也会使方差 \(\sigma^{2}\) 加 大而降低检验的功效. 另一种想法是取差

\[ Z_{i}=X_{i}-Y_{i}, i=1, \cdots, n \]

把 \(Z_{1}, \cdots, Z_{n}\) 视为取自 \(N\left(\mu, \sigma_{1}^{2}\right)\) 的样本 \(\left(\mu\right.\) 作为 \(\theta_{1}-\theta_{2}\) 而 \(\sigma_{1}^{2}\) 可视 为上文的 \(2 \sigma^{2}\). 或者, 根本不必与上文的 \(\theta_{1}, \theta_{2}\) 和 \(\sigma^{2}\) 发生联系)，而 用一样本 \(t\) 检验 (2.17) 去检验假设 \(\mu=0\). 这个做法部分地弥补了 前一做法的缺点,但仍有其问题: 各人在差距如何以分数反映上尺 度也可能不一, 同是感觉上这一点差距, 有人觉得用 5 分的相差就 够了. 而有人可能愿意用 20 分. 这也会破坏上文正态性假设和使 方差 \(\sigma_{1}^{2}\) 增大.

现在看表上最后一行: \(X_{i}-Y_{i}\) 的符号. 这就免除了前面所讲 的可能的缺点, 因为此处只要一个好坏对比的意见, 而不问具体程 度如何,这样就回到了符号检验.

当然, 符号检验也有其缺点, 即它丢失了 \(X_{i}, Y_{i}\) 这些数据中 相当部分的信息,如果有把握认为参试人给分的尺度并无重大差 别, 用 \(t\) 检验比用符号检验很可能给出更高的分辨率. 因此, 要不 要把分数转化为符号, 这是一个个要依据对实际背景的了解去考虑 的问题.

在符号检验中,我们对样本 \(X_{i}, Y_{i}\) 所来自的总体的分布，不 需有什么特殊的假定. 这样的检验在数理统计学上称为“非参数检 验”, 意即它不是只适用于某种特定的参数分布族, 如正态分布族 或指数分布族之类. 非参数方法是数量统计学中的一个重要分支.

顺便说一句: 符号检验中那种回答问题的方式, 是在民意测验 中对某问题作二者取一的回答的那种方式 (你是否赞同某项措施, 两位候选人中你打算投谁的票之类). 在西方每值大选或总统选举 之前, 进行多次民意测验, 每次挑选数百至数干(以至更多) 的人进 行调查. 历史证明: 这种调查与事后的结果惊人地一致. 不懂统计 学的人对此可能觉得难以理解: 一国人民多至千万以至以亿计, 为 什么区区数干人的意见与全体的意见相距如此之近, 其实不难解 释. 以 \(n\) 计调查人数, \(m\) 记某种特定回答 (如准备投 \(A\) 的票) 的人 数, 以 \(m / n=\hat{p}\) 估计 \(p\). 因 \(n\) 甚大, 可以用第四章 (4.13) 式作 \(p\) 的 区间估计, 它大体上就是 \(\hat{p} \pm \mu_{\alpha} \sqrt{\hat{p}(1-\hat{p}) / n}\). 如取 \(n=2500\), \(\alpha=0.05\), 则

\[ \begin{aligned} \mu_{\alpha / 2} \sqrt{\hat{p}(1-\hat{p}) / n} & \leqslant 1.96 \sqrt{\frac{1}{2}\left(1-\frac{1}{2}\right) / 2500} \\ & =1.96 \% \approx 2 \% \end{aligned} \]

即用 \(\bar{p}\) 估计 \(p\),大约只有 \(\pm 2 \%\) 的误差. 如果一个候选人比另一个 领先 5 个百分点,则在民意测验中就能有确定的反映了.

3.2. 6 波哇松分布参数 \(\lambda\) 的检验

设有一个取非负整数值的离散总体, 其分布为包含末知参数 \(\lambda\) 的波哇松分布,如第二章(1.7)式所示. 现设 \(X\) 为抽自该总体的 样本 \({ }^{*}\),要考虑以下的一些检验问题 ( \(\lambda_{0}>0\) 为给定常数):

\[ \begin{array}{ll} 1^{\circ} & H_{0}: \lambda \leqslant \lambda_{0}, H_{1}: \lambda>\lambda_{0} \\ 2^{\circ} & H_{0}^{\prime}: \lambda \geqslant \lambda_{0}, H_{1}^{\prime}: \lambda<\lambda_{0} \\ 3^{\circ} & H_{0}^{\prime \prime}: \lambda=\lambda_{0}, H_{1}^{\prime \prime}: \lambda=\lambda_{0} \end{array} \]

先考虑 \(1^{\circ}\). 由于 \(X\) 的均值为 \(\lambda\), 当 \(H_{0}\) 成立时, \(X\) 倾向于取较 小之值, 由此得出下述直观上合理的检验:

\[ \varphi \text { : 当 } X \leqslant C \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

其功效函数为

\[ \beta_{\varphi}(\lambda)=1-P_{\lambda}(X \leqslant C)=1-\sum_{i=0}^{C_{0}} \mathrm{e}^{-\lambda} \lambda^{i} / i ! \]

× 可以一般地设 \(X_{1}, \cdots, X_{n}\) 为抽自该总体中的样本, 但只要取 \(X=X_{1}+\cdots+X_{n}\), 则据第二章例 \(4.3, X\) 仍为波哇松分布, 只参数政为 \(n \lambda\), 因此, 只抽一个样本的限制并 无损于一般性。 根据第二章习题 \(10, \beta_{\varphi}(\lambda)\) 是 \(\lambda\) 的增加函数. 故为决定 \(C\) 使检验 \(\varphi\) 有给定的水平 \(\alpha\), 只须取 \(C\), 使 \(\beta_{\varphi}\left(\lambda_{0}\right)=\alpha\), 即

\[ \sum_{i=0}^{c} \mathrm{e}^{-\lambda_{0}} \lambda_{0}^{i} / i !=1-\alpha \]

这里也有我们在讲二项分布参数的检验问题时碰到的情况, 即不 一定存在整数 \(C\) 使 (2.49) 恰好成立, 而是存在 \(C_{0}\), 使

\[ \sum_{i=0}^{c} \mathrm{e}^{-\lambda_{0}} \lambda_{0}^{i} / i !<1-\alpha<\sum_{i=0}^{c_{0}^{+1}} \mathrm{e}^{-\lambda_{0}} \lambda_{0}^{i} / i ! \]

这时, 或者调整 \(\alpha\) 之值, 或者施行随机化(当 \(X=C_{0}+1\) 时), 步骤 与以前讲的相同.

适合条件 (2.50) 时 \(C_{0}\) 还可以由等式(第二章习题 10)

\[ \sum_{i=0}^{c_{0}} \mathrm{e}^{-\lambda} \lambda_{0}^{i} / i !=\int_{\lambda_{0}}^{\infty} \mathrm{e}^{-t} t^{c} / c ! \mathrm{d} t \]

通过卡方分布表得出. 事实上, 在上式右端的积分中作变数代换 \(t=x / 2\), 得

\[ \begin{aligned} \frac{1}{c !} \int_{\lambda_{0}}^{\infty} \mathrm{e}^{-t} t^{c} \mathrm{~d} t & =\frac{1}{2^{c+1} c !} \int_{2 \lambda_{0}}^{\infty} \mathrm{e}^{-x / 2} x^{c / 2} \mathrm{~d} x \\ & =\frac{1}{2^{(2 c+2) / 2} \Gamma\left(\frac{2 c+2}{2}\right)} \int_{2 \lambda_{0}}^{\infty} \mathrm{e}^{-x / 2} x^{\frac{2 c+2}{2}-1} \mathrm{~d} x \\ & =1-K_{2 c+2}\left(2 \lambda_{0}\right) \end{aligned} \]

此处 \(K_{2 c+2}(x)\) 为自由度 \(2 c+2\) 的卡方分布函数. 由 (2.49), (2.51) 和 (2.52), 得 \(K_{2 c+2}\left(2 \lambda_{0}\right)=\alpha\), 即

\[ 2 \lambda_{0}=\chi_{2 C+2}^{2}(1-\alpha) \]

然后查 \(\chi^{2}\) 表用试探法. 先取定一个 \(C\) 值查表得出 \(\chi_{2}^{2} C+2(1-\alpha)\). 若此值小于 \(2 \lambda_{0}\), 则表示 \(C\) 取得太小, 反之则太大, 实际上, 从表上 “1- \(\alpha\) ”那一列从上往下看就直接可以找到满足 (2.49) 或 (2.50) 的 \(C\). 例如, 取 \(\lambda_{0}=1.752, \alpha=0.05\), 则 \(2 \lambda_{0}=3.504\). 从 \(\chi^{2}\) 表中头 上为 \(1-\alpha=0.95\) 的那一列往下看, 见到

\[ \chi_{8}^{2}(0.95)=2.733, \chi_{10}^{2}(0.95)=3.940 \]

故满足 (2.50) 的 \(C_{0}\) 为 \(C_{0}=3\). 这个方法的缺点是: 它没有给出 (2.50) 左、名两端之值. 因而在 \(C_{0}+1\) 处施行随机化时的概率 (即 例 2.3 中 0.767 这个数) 算不出来 (如果所用的 \(\chi^{2}\) 表的表头上恰 有“ \(2 \lambda_{0}\) ”这一栏, 当然就不成问题).

例 2.4 假定一指定地区内的人口中, 每年患某种特殊疾病 的人数服从波哇松分布, 且过去相当长一段时间, 平均每年发病人 数为 2.3 人. 但近 4 年内记录到的发病人数分别为 \(3,4,1,5\). 问是 否有明显证据表明发病率上升了?

从数字上看, 发病率的上升甚为明显. 从统计学的角度观察问 题, 就是要检验一下这表面上的增加是否达到了在一定水平 \(\alpha\) 之 下的显著性, 即不能仅从偶然波动的角度去解释

为此, 以 \(\lambda \leqslant 2.3\) 作为原假设, 把 4 个年份的数字相加, 得 \(X\) \(=3+4+1+5=13\). 要注意 \(X\) 的分布为参数是 \(4 \lambda\) 的波哇松分布, 因此据 \(X\) 去进行检验时, 原假设要改为 \(\lambda \leqslant \lambda_{0}=4 \times 2.3=9.2\). 取 \(\alpha=0.05\). 查表有

\[ \chi^{\frac{2}{30}}(0.95)=18.493>2 \lambda_{0}, \chi_{28}^{2}(0.95)=16.928<2 \lambda_{0} \]

由此知应当在 \(X \leqslant 13\) 时接受 \(\lambda \leqslant 9.2, X \geqslant 15\) 时否定 \((X=14\) 要施 行随机化, 或把 14 放到否定域内). 总之, 按所得数据 \(X=13\) 尚不 能否定“年平均发病人数末上升”之假设。

若取 \(a=0.20\), 则查表得

\[ \chi_{26}^{2}(0.80)=19.820>2 \lambda_{0}, \chi_{24}^{2}(0.80)=18.062<2 \lambda_{0} \]

相当于 \((2.50)\) 式中的 \(C_{0}=11\), 现 \(X=13\), 该否定原假设 \(\lambda \leqslant 9.2\).

随着所取水平 \(a\) 的不同, 在同一数据下一个假设的接受与否 也可以不同, 而水平的选择是人为的. 由此可知, 不能把检验的结 果按其表面意义解释得太死. 拿本例而言, 如果你认为事态并非很 严重, 而采纳“发病人数增加”的结论将导致需要巨额经费的措施, 你可以慎重一些而采取一个较低的水平, 如 \(\alpha=0.05\). 这时你的结 论是: 目前尚无十分有力的证据表明情况已恶化了, 可再观察一段 时间. 但如你只是把这个问题作为一个单纯的科研题目, 你也许会 倾向于认为不必过于保守, 即宁取较大一点的水平, 例如 \(\alpha=\) 0.20 . 这时你的结论将是: 已有较充分的证据表明情况有了恶化, 值得注意,采取这个看法犯错误的机会不超过 0.2. 这两种看法并 无矛盾. 恰恰相反,也许这两种看法的结合, 使我们对本题中随机 性的影响如何,得到了更深人一步的理解.

对问题 \(2^{\circ}\) 和 \(3^{\circ}\), 类似的讨论得到水平 \(\alpha\) 的检验 \(\varphi^{\prime}\) 与 \(\varphi^{\prime \prime}\) 如下:

\(\varphi^{\prime}\) : 当 \(X \geqslant C\) 时接受 \(H_{0}^{\prime}\), 不然就否定 \(H_{0}^{\prime}\)

其中 \(C\) 由关系式

\[ \sum_{i=0}^{C-1} \mathrm{e}^{-\lambda_{0}} \lambda_{0}^{i} / i !=\alpha \]

确定，或用

\[ \begin{gathered} 2 \lambda_{0}=\chi_{2 C}^{2}(\alpha) \\ \varphi^{\prime \prime} \text { : 当 } C_{1} \leqslant X \leqslant C_{2} \text { 时接受 } H_{0}^{\prime \prime} \text {, 不然就否定 } H_{0}^{\prime \prime} \end{gathered} \]

\(C_{1}, C_{2}\) 分别由

确定,或用

\[ \sum_{i=0}^{C_{1}-1} \mathrm{e}^{-\lambda_{0}} \lambda_{0}^{i} / i !=\alpha / 2, \sum_{i=0}^{C_{2}} \mathrm{e}^{-\lambda_{0}} \lambda_{0}^{i} / i !=1-\alpha / 2 \]

\[ 2 \lambda_{0}=\chi_{2 C_{1}}^{2}(\alpha / 2), 2 \lambda_{0}=\chi_{2 C_{2}+2}^{2}(1-\alpha / 2) \]

波哇松分布参数检验有一个有趣的应 用, 即用于本节 (5.2.4)中讲过的定时截尾 寿命检验的情形. 前面我们讲的定时截尾 是预定一个时刻 \(T_{0}\), 在时刻 0 时对 \(n\) 个 元件 (其寿命都服从参数为 \(\lambda\) 的指数分 布)进行测试. 每个参试元件如在时刻 \(T_{0}\) 前失效,则记下其失效时刻而并不替换该

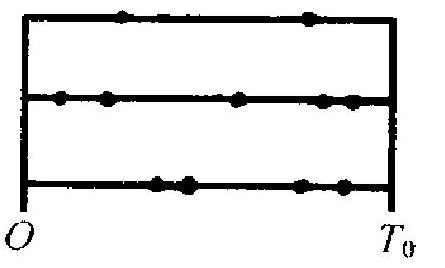
• 元件失效时刻 图 5.4 元件. 现在对试验作一点修改: 开始时 \(n\) 个元件参试,不论在 \(T_{0}\) 之前的哪个时刻其中哪个元件失效了, 就立即用一个新的替换上 去. 到时刻 \(T_{0}\) 时结束试验, 把到那时为止失效的元件总数记为 \(X\). 如图 5.4 , 表示在时刻 0 有 3 个元件参试, 到时刻 \(T_{0}\) 结束, 共 有 \(X=11\) 个元件失效.

用第二章习题 25 容易推出: \(X\) 服从参数 \(\nu=n T_{0} \lambda\) 的波哇松 分布. 如要检验 “元件平均寿命不小于 \(1 / \lambda_{0}\) ” 即 “ \(\lambda \leqslant \lambda_{0}\) ”, 可归结为 在波哇松总体中观察了 \(X\), 要检验假设 “ \(\nu \leqslant n T_{0} \lambda_{0}\) ”. 这正是我们 讨论过的问题.

3.3. 7 大样本检验

在上面讲的一些检验问题中, 我们都知道了有关检验统计量 的确切分布. 据此, 就可以在给定的检验水平 \(\alpha\) 之下, 决定检验统 计量的临界值, 即我们前面多次提到的常数 \(C\) (或 \(C_{1}, C_{2}\), 如在双 侧情形).

但在不少问题中, 检验统计量在直观上看合理,但其确切分布 求不出. 这时, 往往就求助于其极限分布, 依据它去决定临界值 \(C\). 举一个例子。

例 2.5 (贝伦斯-费歇尔问题) 设 \(X_{1}, \cdots, X_{n}\) 和 \(Y_{1}, \cdots, Y_{m}\) 分别是抽自正态总体 \(N\left(\theta_{1}, \sigma_{1}^{2}\right)\) 和 \(N\left(\theta_{2}, \sigma_{2}^{2}\right)\) 的样本. \(\theta_{1}, \sigma_{1}^{2}, \theta_{2}, \sigma_{2}^{2}\) 全都末知,也没有假定 \(\sigma_{1}^{2}\) 与 \(\sigma_{2}^{2}\) 相等. 要检验原假设 “ \(\theta_{1}=\theta_{2}\) ”, 对 立假设是 “ \(\theta_{1} \neq \theta_{2}\) ”. 也可以考虑单侧的情形, 即 “ \(\theta_{1} \leqslant \theta_{2}\) ”为原假 设.

据正态分布的性质有

\[ \frac{(\bar{X}-\bar{Y})-\left(\theta_{1}-\theta_{2}\right)}{\sqrt{\sigma_{1}^{2} / n+\sigma_{1}^{2} / m}} \sim N(0,1) \]

因为 \(\sigma_{1}^{2}, \sigma_{2}^{2}\) 末知, 虽则 (2.60) 为确切分布, 仍无法据以确定检验的 临界值. 于是以 \(X\) 样本的样本方差 \(S_{1}^{2}\) 作为 \(\sigma_{1}^{2}\) 的估计, 以 \(Y\) 样本 的样本方差 \(S_{2}^{2}\) 作为 \(\sigma_{2}^{2}\) 的估计, 分别取代 (2.60) 中的 \(\sigma_{1}^{2}\) 和 \(\sigma_{2}^{2}\) 得 到

\[ T=\frac{(\bar{X}-\bar{Y})-\left(\theta_{1}-\theta_{2}\right)}{\sqrt{S_{1}^{2} / n+S_{2}^{2} / m}} \]

其确切分布很复杂, 但当 \(n, m\) 都较大时, 其分布接近 \(N(0,1)\). 姑 且认为它就是 \(N(0,1)\), 则得到原假设 \(\theta_{1}=\theta_{2}\) 的下述检验法: 当

\[ |\bar{X}-\bar{Y}| / \sqrt{S_{1}^{2} / n+S_{2}^{2} / m} \leqslant u_{\alpha / 2} \]

时接受原假设,不然就否定.

大样本检验,例如 (2.62), 在下述意义下是近似的: 原先预定 的检验水平是 \(\alpha\), 而该检验的实际水平与 \(\alpha\) 有差距. 这是由于 (2.61) 式的 \(T\) 的分布与 \(N(0,1)\) 的分布有距离. 如果 \(n\) 和 \(m\) 都较 大,则 \(T\) 的分布与 \(N(0,1)\) 的差异就很小, 而检验 \((2.62)\) 的实际水 平就与其预定水平 \(\alpha\) 相差很小. 问题在于, 我们一般并不清楚对 一定的 \(n\) 和 \(m, T\) 的分布与 \(N(0,1)\) 的差异有多大, 因而也就不能 估计检验的实际水平与其名义水平究竟差多少. 在区间估计中也 有这个问题: 由于使用了有关变量的近似分布,所作出的区间估 计, 其实际置信系数与名义 (预定的) 置信系数之间, 有一个我们不 了解的差距.

因此,大样本方法是一个 “不得已而为之”的办法,只要有基于 精确分布的方法 (小样本方法), 我们总是乐于采用的, 可惜的是: 在数理统计学的许多问题中,能找出形式足够简单且便于使用的 精确分布的情况, 到底还是不多. 因此,大样本方法在数理统计学 中占有重要的地位.

也有的情况, 精确分布是知道的, 但在样本大小 \(n\) 太大时, 计 算不便, 我们也时常用其较简单的极限分布去取代之.下面是一个 例子.

例 2.6 再考虑 5.2.5 段讨论过的二项分布参数 \(p\) 的检验 问题. 以该处的问题 \(3^{\circ}\) (原假设 \(p=p_{0}\) ) 为例, 前面我们已找出检 验 (2.45), 其中 \(C_{1}, C_{2}\) 由 (2.46) 决定. 当 \(n\) 很大时, (2.46) 中的和 无法从二项分布表上查得,因而 \(C_{1}, C_{2}\) 的决定就不易.

但根据中心极根定理 (第三章定理 4.3 ), 当原假设 \(p=p_{0}\) 成 立而 \(n \rightarrow \infty\) 时, \(\left(X-n p_{0}\right) / \sqrt{n p_{0}\left(1-p_{0}\right)}\) 的分布趋向于 \(N(0\), \(1)\). 近似地就把 \(N(0,1)\) 作为其分布, 则可提出如下的检验: 当

\[ \left|\left(X-n p_{0}\right)\right| / \sqrt{n p_{0}\left(1-p_{0}\right)} \leqslant u_{\alpha / 2} \]

即

\[ n p_{0}-u_{\alpha / 2} \sqrt{p_{0}\left(1-p_{0}\right)} \leqslant X \leqslant n p_{0}+u_{\alpha / 2} \sqrt{p_{0}\left(1-p_{0}\right)} \]

时接受原假设 \(p=p_{0}\), 不然就拒绝.与 (2.45) 比较, 这等于以 (2.63) 两端之值作为 \(C_{1}\) 和 \(C_{2}\) 的近似值. 这两个值比 \(C_{1}, C_{2}\) 的 确切值 (由 (2.46) 决定的)要容易计算得多.

我们再提醒一下以前曾解释过的一件事情: 统计方法的大小 样本之分, 不在于样本大小 \(n\) 多大(这无清楚界线), 而全看其是 否使用有关变量的极限分布. 拿本例而言, 若用检验 (2.63), 无论 \(n\) 多小, 总是大样本方法; 若用检验 (2.45) 而 \(C_{1}, C_{2}\) 由 (2.46) 㹟 定,则无论 \(n\) 多大, 仍是小样本方法.

3.4. 8 贝叶斯方法

贝叶斯方法的一般原则已经在 4.2 节 4.2.4 段中阐述过, 并 已曾用于点估计和区间估计问题.贝叶斯方法用于检验问题至为 简单: 如已经选定了先验分布, 则在有了样本 \(X_{1}, \cdots, X_{n}\) 后,分别 算出原假设 \(H_{0}\) 的条件概率 \(P\left(H_{0} \mid X_{1}, \cdots, X_{n}\right)\) 和对立假设 \(H_{1}\) 的 条件概率 \(P\left(H_{1} \mid X_{1}, \cdots, X_{n}\right)\). 若前者大于后者, 则接受原假设 \(H_{0}\); 若后者大于前者，则否定原假设 \(H_{0}\) ，如果二者相等(都等于 \(1 /\) 2 ), 则可让其悬而不决 (留待进一步考察), 或随机地取其一, 举例 说明之.

例 2.7 考虑第四章例 2.14 , 但此处我们讨论有关 \(\theta\) 的检验 问题.

\(1^{\circ}\) 设原假设 \(H_{0}: \theta \leqslant 0\), 对立假设 \(H_{1}: \theta>0\), 就该例给的先验 分布 \(N\left(\mu, \sigma^{2}\right)\), 已求出后验分布为正态 \(N\left(t, \eta^{2}\right)\), 其中 \(t, \eta^{2}\) 分别 见第四章 (2.17) 和(2.18) 式.

当 \(\theta \sim N\left(t, \eta^{2}\right)\) 时, \(\theta \leqslant 0\) 的概率易算出, 此处我们只关心它 是否小于 \(1 / 2\). 显然, 若 \(t>0\), 此概率小于 \(1 / 2\), 若 \(t<0\), 则大于 \(1 /\) 2 . 当 \(t=0\) 时则恰为 \(1 / 2\). 因此, 得出在所给先验分布之下的贝叶 斯检验为:

\[ \left\{\begin{array}{l} \text { 当 } t<0 \text { 即 } \bar{X}<-\mu /\left(n \sigma^{2}\right) \text { 时接受 } H_{0}: \theta \leqslant 0 \\ \text { 当 } t>0 \text { 即 } \bar{X}>-\mu /\left(n \sigma^{2}\right) \text { 时否定 } H_{0} \\ \text { 当 } t=0 \text { 即 } \bar{X}=-\mu /\left(n \sigma^{2}\right) \text { 时,悬而不决 } \end{array}\right. \]

从其中看出先验信息的影响. 设 \(\mu>0\), 则先验信息较有利于 \(H_{1}\) : \(\theta>0\). 所产生的后果是: \(\bar{X}\) 必须小于一个比 0 更小的数 \(-\mu /\) \(\left(n \sigma^{2}\right)\), 才能接受 \(\theta \leqslant 0\),若无这一先验信息的“先人之见”,则公平 的看法是 : 当 \(\bar{X}<0\) 时认为 \(\theta \leqslant 0\) 的可能性较大,因而接受它. 先验 信息的存在使我们要求更强的证据.从其影响上看, 与选择检验水 平 \(\alpha\) 有其相通之处: 我们愈是相信原假设, 就愈是倾向于选择较 低的 \(\alpha\), 而使检验更有利于原假设. 当然,这只是一个比喻. 在贝叶 斯方法中没有“检验水平” 的概念, 其方法的精神与奈曼一皮尔逊理 论根本不同.

\(2^{\circ}\) 若取原假设为 \(H_{0}: \theta_{1} \leqslant \theta \leqslant \theta_{2}\left(\theta_{1}, \theta_{2}\right.\) 给定), 则原则上完 全一样: 在 \(\theta-N\left(t, \eta^{2}\right)\) 时, 算出 \(\theta_{1} \leqslant \theta \leqslant \theta_{2}\) 的概率为

\[ P\left(\theta_{1} \leqslant \theta \leqslant \theta_{2} \mid X_{1}, \cdots, X_{n}\right)=\Phi\left(\frac{\theta_{2}-t}{\eta}\right)-\Phi\left(\frac{\theta_{1}-t}{\eta}\right) \]

我们留给读者去证明: 这函数作为 \(t\) 的函数, 当 \(t\) 由 \(-\infty\) 升至 \(\infty\) 时,先增后减. 由此可知, 使此表达式大于 \(1 / 2\) 的 \(t\) 是落在某区间 \((a, b)\) 内 (可以是空集). 相应地, \(\bar{X}\) 落在某区间 \((A, B)\) 内, 即贝叶 斯检验为:

\[ \left\{\begin{array}{l} \text { 当 } A<\bar{X}<B \text { 时, 接受原假设 } H_{0}: \theta_{1} \leqslant \theta \leqslant \theta_{2} \\ \text { 当 } \bar{X}<A \text { 或 } \bar{X}>B \text { 时,否定 } H_{0} \\ \text { 当 } \bar{X}=A \text { 或 } B \text { 时, 悬而不决 } \end{array}\right. \]

用非贝叶斯方法, 即奈曼一皮尔逊的方法, 也可以得到形式一 样的检验, 但临界值不同, 这留作为一个三题.

\(3^{\circ}\) 最后考虑检验问题 \(H_{0}: \theta=0, H_{1}: \theta \neq 0\). 因为后验分布为正态, \(\theta\) 取一个值 0 的后验概率为 \(0: P\left(H_{0}\right.\) \(\left.\mid X_{1}, \cdots, X_{n}\right)\) 总为 0 . 故依贝叶斯检验, 不论样本如何, 总要否定 \(H_{0}\).

这样的解看来很不吸引人. 这里面就有些思想得弄清楚.

首先, 就贝叶斯方法而言, 它只看后验概率的大小. 0 这个值 的先验概率为 0 , 即根本不可能之事, 就是说, 先天地已知道 “ \(\theta=\) 0 ”不可能, 还有什么值得去检验的。

问题就出在这个“绝对”上. 如果你要检验某个物件的重量“绝 对地”等于 2.567959 克, 我说你不必检验, 世间找不出其重量与 2.567959 克一丝不差的物体. 在这个意义上,你可以不经检验否 定 \(\theta=\theta_{0}\) 这种假设, 可是在实用中, 人们并不这么绝对的看问题. 当人们检验 \(\theta=\theta_{0}\) 这假设时,他是理解为: 所检验的其实是: \(\theta\) 在 \(\theta_{0}\) 附近一个可允许的限度内, 且只要样本中包含的证据不与这一 点相去太远, 就可考虑接受. 这是我们日常处理这种问题的看法. 我们以前讲过的, 以奈曼一皮尔逊思想为基础的检验法, 很好地体 现了这一点.

在此,如一定要用贝旪斯方法来检验 \(\theta=0\) 这个假设,就必须 给 0 这个点以一正的先验概率 \(p_{0}\). 剩下的 \(1-p_{0}\) 的概率以某种方 式分布在 \(\theta \neq 0\) 的范围内, 例如按正态分布. 此处不涉及细节, 有 兴趣的读者可参看陈希擩、倪国熙合著的《数理统计学教程》p. 204 例 5.8. 大家可能觉得: \(p_{0}\) 这个值毫无定准, 如何给法? 在并无确 实的先验信息可依时, 只好凭考虑两类错误的后果去选择: 如果你 认为错误地否定 \(\theta=0\) 后果较严重, 你可以选择一个略大的 \(p_{0}\), 以 使“ \(\theta=0\) ”难于被否定一些. 这与在奈曼一皮尔逊方法中选择检验 水平 \(\alpha\) 有同一效应一须知, 水平 \(\alpha\) 的选定也并无理论依据, 而 是基于实际考虑. 此处 \(p_{0}\) 的选择,不妨也作如是观.

贝叶斯方法的最大的好处是: 一经选定了先验分布, 则剩下的 只是计算问题, 而没有找检验统计量的问题, 特别是没有找检验统 计量的精确分布的问题,看一个例子. 例 2.8 设 \(X_{1}, \cdots, X_{n}\) 为抽自正态总体 \(N\left(\theta, \sigma^{2}\right)\) 的样本, \(\theta\) 和 \(\sigma\) 都末知, 考虑检验问题

\[ H_{0}: a \leqslant \theta \leqslant b, H_{1}: \theta<a \text { 或 } \theta>b . \]

其中 \(a, b\) 都是给定的有限常数, \(a<b\).

在本节 (5.2.1) 段中, 我们曾讨论过 \(\theta \leqslant \theta_{0}, \theta \geqslant \theta_{0}\) 和 \(\theta=\theta_{0}\) 等 原假设的检验问题,但就是没有提到过 (2.66), 其实这个问题在应 用上也有其重要性. 原因就在于: 用非贝叶斯的方法, 这个检验所 涉及的分布问题不易解决.

现用贝叶斯法, 给 \(\theta\) 以广义先验密度 1 , 给 \(\sigma\) 以广义先验密度 \(\sigma^{-1}\), 并设二者独立. 这等于说给 \((\theta, \sigma)\) 以广义先验密度 \(\sigma^{-1}\), 当 \(-\infty<\theta<\infty, \sigma>0\). 由第四章 (2.10) 和 (2.11) 式, 得知在有了样 本 \(X_{1}, \cdots, X_{n}\) 时 \((\theta, \sigma)\) 的后验密度为

\[ C_{n} \sigma^{-(n+1)} \exp \left[-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-\theta\right)^{2}\right](-\infty<\theta<\infty, \sigma>0) \]

这里

\[ C_{n}=\left(\int_{0}^{\infty} \int_{-\infty}^{\infty} \sigma^{-(n+1)} \exp \left[-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-\theta\right)^{2}\right] \mathrm{d} \theta \mathrm{d} \sigma\right)^{-1} \]

\(C_{n}\) 是一个与 \(\theta, \sigma\) 无关但与样本有关的常数, 以下的常数 \(D_{n}, E_{n}\) 等也如此, 它们没有必要去计算. 将 (2.67) 对 \(\sigma\) 从 0 到 \(\infty\) 积分, 得 到 \(\theta\) 的边缘后验密度, 为

\[ \begin{aligned} & C_{n} \int_{0}^{\infty} \sigma^{-(n+1)} \exp \left[-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(X_{i}-\theta\right)^{2}\right] \mathrm{d} \sigma \\ & \quad=D_{n}\left(\sum_{i=1}^{n}\left(X_{i}-\theta\right)^{2}\right)^{-n / 2}=D_{n}\left(S_{0}^{2}+n(\bar{X}-\theta)^{2}\right)^{-n / 2} \\ & \quad=D_{n} S_{0}^{-n}\left[1+n(\bar{X}-\theta)^{2} / S_{0}^{2}\right]^{-n / 2} \\ & \quad=E_{n}\left[1+n(\bar{X}-\theta)^{2} /(n-1) S^{2}\right]^{-n / 2} \end{aligned} \]

其中 \(S_{0}^{2}\) 为 \(\sum_{i=1}^{n}(X-\bar{X})^{2}\), 即 \((n-1) S^{2}, S^{2}\) 为样本方差. \(S_{0}, S\) 都 与 \(\sigma, \theta\) 无关. 令

\[ \theta^{*}=\sqrt{n}(\theta-\bar{X}) / S \]

它是 \(\theta\) 的线性函数. 由 \(\theta\) 有密度 (2.68), 易算出 \(\theta^{*}\) 有密度函数

\[ F_{n}\left(1+\frac{\theta^{* 2}}{n-1}\right)^{-n / 2},-\infty<\theta^{*}<\infty \]

把这个表达式和第二章 (4.31) 式比较, 即知它是自由度为 \(n-1\) 的 \(t\) 分布密度, 因而常数 \(F_{n}\) 就必然是 \(\Gamma\left(\frac{n}{2}\right) /\left(\sqrt{2 \pi} \Gamma\left(\frac{n-1}{2}\right)\right)\). 以 \(T_{n-1}\) 记自由度 \(n-1\) 的 \(t\) 分布函数,用 (2.69), (2.70), 即得

\[ \begin{aligned} & P\left(H_{0} \mid X_{1}, \cdots, X_{n}\right)=P\left(a \leqslant \theta \leqslant b \mid X_{1}, \cdots, X_{n}\right) \\ = & P\left(\sqrt{n}(a-\bar{X}) / S \leqslant \theta^{*} \leqslant \sqrt{n}(b-\bar{X}) / S \mid X_{1}, \cdots, X_{n}\right) \\ = & T_{n-1}\left(\frac{\sqrt{n}(b-\bar{X})}{S}\right)-T_{n-1}\left(\frac{\sqrt{n}(a-\bar{X})}{S}\right) \end{aligned} \]

看它是否大于 \(1 / 2\), 即决定是否接受原假设 \(H_{0}\).

例如, 取原假设为 \(-1 \leqslant \theta \leqslant 1\), 样本大小 \(n=16\), 且设由样本算 出 \(\bar{X}=0.8, S=2\). 则

\[ \begin{aligned} & \sqrt{n}(b-\bar{X}) / S=4(1-0.8) / 2=0.4 \\ & \sqrt{n}(a-\bar{X}) / S=4(-1-0.8) / 2=-3.6 \end{aligned} \]

因而

\[ P\left(-1 \leqslant \theta \leqslant 1 \mid X_{1}, \cdots, X_{n}\right)=T_{15}(0.4)-T_{15}(-3.6) \]

查 \(t\) 分布表知上式右边为 \(0.621119-0.086245=0.537874>\) \(1 / 2\). 故应当接受原假设.

有意思的是看 (2.69) 式的 \(\theta^{*}\), 若回到非贝叶斯的看法, 即把 \(\bar{X}, S\) 看作是随机的而 \(\theta\) 为末知常数,则如第二章 (4.34) 所示, \(\theta^{*}\) 的分布为自由度 \(n-1\) 的 \(t\) 分布 \(t_{n-1}\). 刚才我们又证明了: 在所给 的 (广义) 先验密度之下, \(\theta^{*}\) 的后验分布是 \(t_{n-1}\), 殊途而同归,但解 释截然不同. 在非贝叶斯意义下得到的 \(\theta^{*} \sim t_{n-1}\) 无助于解决此处 的检验问题, 而在贝叶斯方法之下, 由 \(\theta^{*}\) 的后验分布为 \(t_{n-1}\) 立即 导致检验问题的解.

顺便交代一下: 30 年代初, R. A. 费歇尔从非贝叶斯的结果

\[ \sqrt{n}(\bar{X}-\theta) / S-t_{n-1} \]

出发, 用如下的推理: 在上式中把 \(\bar{X}, S\) 看作已知常数而将 \(\theta\) 看成 是随机的, 则 (2.71) 式可看作决定了 \(\theta\) 的一个分布, 他称之为 \(\theta\) 的 信仰分布 (fiducial distribution). 其解释如下: 在抽样前, 我们对 \(\theta\) 茫然无所知. 有了样本后, 仍不能确切地定出 \(\theta\). 但根据样本所提 供的信息,我们对 \(\theta\) 取各种值的“信仰程度”有了不同: 例如,我们 相信 \(\theta\) 取 \(\bar{X}\) 附近值的程度, 比相信 \(\theta\) 取远离 \(\bar{X}\) 的值的程度要大 些. 信仰分布从数量上刻画了这个相信程度. 若以 \(F\) 记 \(\theta\) 的信仰 分布, 则 \(F(b)-F(a)\) 就是我们对 “ \(\theta\) 落在区间 \((a, b)\) 内” 的信仰 概率 (fiducial probability). 利用这个就可以进行统计推断——作 区间估计, 检验等, 这个方法在数理统计学中称为信仰推断法 (fiducial inference).

费歇尔的思想与贝叶斯学派的基本思想有共同之处, 即都是 把末知参数视为随机变量, 可以谈论其概率分布. 二者不同之处在 于贝叶斯学派要求先验分布而费歇尔不要求. 贝叶斯方法中的后 验分布与费歇尔的信仰分布可以作等量观, 但是, 在贝叶斯方法 中, 由先验分布到后验分布有一定的规则遵循, 即求条件分布的规 则. 因此, 一旦先验分布指定了, 后验分布并无岐义. 费歇尔的信仰 分布则不然, 它虽不依赖什么先验分布, 但不仅无一定的法则可遵 循, 且在较复杂的场合, 简直不知从何着手. 正是由于这个原因, 信 仰推断的方法没有能推开来, 与频率学派和贝叶斯学派鼎足而三. 但是，这方法在有些情况下有其应用，特别是在我们多次提到过的 贝伦斯一费歇尔问题中, 此方法颇为成功 (参看前引陈希孺、倪国 熙书 p. 182-183), 目前仍有些学者对它进行研究.

再回过头说说贝叶斯检验. 上面提到的那个准则, 即在 \(P\left(H_{0}\right.\) \(\left(X_{1}, \cdots, X_{n}\right)>1 / 2\) 时接受原假设, 并非一成不变的. 在实际问题 中, 不论接受或是否定 \(H_{0}\), 往往都意味着一种可能带来经济上或 其他方面后果的行动. 由于后果的严重性不同及当事者的承受力 不同, 他在作出决定时所采用的 “临界概率” 就不一定是 \(1 / 2\), 可以 大一些或小一些. 举例言之: 接受 \(H_{0}\) 表示兴办某一商业活动. 这 活动一旦成功, 大有利可图, 但也很可能失败而招致一定的经济损 失.一个有实力能承担这样的风险且又富于冒险精神的实业家, 可 能决定只要在 \(30 \%\) 的成功机会就准备一试, 这时他把接受 \(H_{0}\) 的 标准定为 \(P\left(H_{0} \mid X_{1}, \cdots, X_{n}\right) \geqslant 0.3\). 反之, 一个实力不强且较稳健 的人, 也许会要求有八成把提才干. 这已不单纯是统计推断问题, 而是一种统计决策问题, 其特点是不仅要考虑到样本提供的信息, 还须考虑到种种决定可能带来的后果 *

评论

登录github的账号后，可以直接在下方评论框中输入。

如果想进行更详细的讨论(如排版、上传图片等)，选择一个反应后并点击上方的文字，进入论坛页面。