答案⚓︎

\(1.1^{\circ} \beta(\theta)=1-\left[\Phi\left(\frac{C_{2}-\theta}{\sigma}\right)-\Phi\left(\frac{C_{1}-\theta}{\sigma}\right)\right] . \Phi\) 为标准正态 \(N(0,1)\) 的分布函数.

\(2^{\circ}\) 这归结为方程组

\[ \begin{aligned} & \Phi\left(\frac{C_{2}-a}{\sigma}\right)-\Phi\left(\frac{C_{1}-a}{\sigma}\right)=1-\alpha \\ & \Phi\left(\frac{C_{2}-b}{\sigma}\right)-\Phi\left(\frac{C_{1}-b}{\sigma}\right)=1-\alpha \end{aligned} \]

这方程组可以用如下的叠代方式, 借助于正态分布表求解: 指定 \(C_{1}\) 的一个初始值 \(C_{1}^{0}\). 由 (1),(2) 分别决定出 \(C_{1}\) 的各一个值, 若二者差距不在容许范围内, 其算术平均取为 \(C_{2}^{0}\) 以 \(C_{2}^{0}\) 代人 \((1),(2)\), 分别解出两个 \(C_{1}\) 值. 若二者差距不在容许范围内, 其算术平均取为 \(C_{1}\) 的下一个值 \(C_{1}^{1}\). 然后以 \(C_{1}^{1}\) 代入 \((1),(2)\) 中之 \(C_{1}\), 定出 \(C_{2}\) 之下一个值 \(C_{2}^{\prime}\). 这样继续到某肷定出的两个值差距在容许范围内为止.

\[ 3^{\circ} \text { 记 } \Phi^{\prime}(x)=\varphi(x)=\frac{1}{\sqrt{2 \pi}} \mathrm{e}^{-x^{2} / 2} \text {, 易见 } \beta(\theta) \text { 的导数为 } \]

388 •

\[ \beta^{\prime}(\theta)=\frac{1}{\sigma}\left[\varphi\left(\frac{C_{2}-\theta}{\sigma}\right)-\varphi\left(\frac{C_{1}-\theta}{\sigma}\right)\right] \]

由 \(\varphi(x)\) 的形式易看出: \(\theta<\frac{C_{1}+C_{2}}{2}\) 时 \(\beta^{\prime}(\theta)<0\), 当 \(\theta>\frac{C_{1}+C_{2}}{2}\) 时 \(\beta^{\prime}(\theta)>\) 0 , 故 \(\beta(\theta)\) 当 \(\theta\) 由 \(-\infty\) 变到 \(\infty\) 时, 先下降到 \(\left(C_{1}+C_{2}\right) / 2\) 点处达到最小值, 然后上升 (见图 7). 由于 \(\beta(a)=\beta(b)\), 看出 \(a<\left(c_{1}+c_{2}\right) / 2<b\), 而在 \([a, b]\) 区

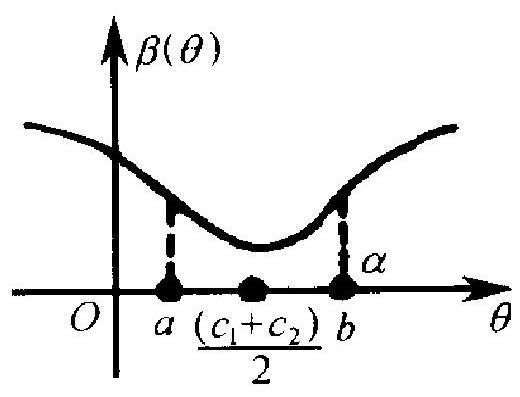间内, \(\beta(\theta)\) 之值不大于 \(a\).

注: 显然, \(\beta(\theta)\) 的图形关于点 \(\left(c_{1}+c_{2}\right) / 2\) 对称, 由此可知, \(a\), \(b\) 与 \(\left(c_{1}+c_{2}\right) / 2\) 有等距离, 这说明必有 \(c_{1}+c_{2}=a+b\). 这个事实提供了解方程组 (1), (2) 的一种 “try and error” 的方法: 取 \(c_{1}\) 的初始值 \(c_{1}^{0}<(a+b) / 2\). 由 \(c_{2}^{0}=(a+b)-c_{1}^{0}\) 定出 \(c_{2}\) 的初始值 \(c_{2}^{0}\). 以这两值代人(1), (2), 若右边小于 \(1-\alpha\), 说明 \(c_{1}^{0}\) 选得太大, 否则就选得太小, 经几步纠正达到接近相等为止.

\(4^{\circ}\) 此由 \(\lim _{x \rightarrow-\infty} \Phi(x)=0\) 及 \(\lim _{x \rightarrow \infty} \Phi(x)=1\) 立即得出. 表示当 \(\theta\) 之真值与原假设距离愈来愈远时, 本检验以愈来愈确定的把握否定之。

依直观考虑, 检验取为“当 \(c_{1} \leqslant \bar{X} \leqslant c_{2}\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\) ”. 利用 \(2 n \lambda \bar{X} \sim \chi^{2} n\), 一切与第一题相似, 在求解 \(c_{1}, c_{2}\) 时要用到精细的卡方分布表才行.
令 \(T=\sqrt{\frac{m n}{m+n}}(\bar{X}-\bar{Y}) / \sigma\). 证明: 当原假设成立时有 \(T \sim N(0,1)\). 由此作出检验: 当 \(|T| \leqslant u_{a / 2}\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\).

算出其功效函数为

\[ \beta(a, b)=1-\left[\Phi\left(u_{a / 2}-\sqrt{\frac{m n}{m+n}} \frac{d}{\sigma}\right)\right. \]

\[ \left.-\Phi\left(-u_{a / 2}-\sqrt{\frac{m n}{m+n}} \frac{d}{\sigma}\right)\right] \]

其中 \(d=a-b\). 令上式右端为 \(1-d_{2}\), 解出 \(d\) 之值 (有两个: \(\pm d_{1}\) ) 其正解即所求之 \(d_{1}\).

\(\bar{X}-c \bar{Y}-N\left(a-c b, \frac{m+n c^{2}}{m n} \sigma^{2}\right)\) 仿照两样本 \(t\) 检验的得出过程, 作统计量

\[ \begin{aligned} & T= \sqrt{\frac{m n(m+n-2)}{m+n c^{2}}(\bar{X}-c \bar{Y})} \\ & \sqrt{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}+\sum_{j=1}^{m}\left(Y_{j}-\bar{Y}\right)^{2}} \end{aligned} \]

而得出当 \(H_{0}\) 成立时 \(T \sim t_{m+n-2}\). 由此得出检验: 当 \(|T| \leqslant\) \(t_{m+n-2}(\alpha / 2)\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\).

作变换 \(X_{i}^{\prime}=c X_{i}, \cdots, i=1, n\). 考虑两组样本

\[ X_{1}^{\prime}, \cdots, X_{n}^{\prime} \text { 和 } Y_{1}, \cdots, Y_{m} \]

它们都有正态分布, 等方差 \(\sigma_{2}^{2}\), 但 \(X_{i}^{\prime}\) 之均值为 \(a^{\prime}=c a, Y_{j}\) 之均值为 \(b\). 故就样本 (3) 而言, 原来的假设 \(H_{0}\) 转化为 \(a^{\prime}=c b\). 因而转化为第 4 题.

利用 \(\lambda_{1} \bar{X} /\left(\lambda_{2} \bar{Y}\right) \sim F_{2 n, 2 m}\) 这个事实.
记 \(T=\max \left(X_{1}, \cdots, X_{n}\right)\). 从直观上看, \(\theta\) 愈大, \(T\) 也愈倾向于取大值. 故一个合理的检验为: 当 \(T \leqslant C\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\). 为定 \(C\), 计算其功效函数 (这用到 \(T\) 的分布, 参考第二章 22 题)

\[ \beta(\theta)=P(T>C)=1-(C / \theta)^{n} \]

它是 \(\theta\) 的增函数, 故为使 \(\beta(\theta) \leqslant \alpha\) 当 \(\theta \leqslant \theta_{0}\), 只须使 \(\beta\left(\theta_{0}\right)=\alpha\) 即可. 这定出 \(C=(1-\alpha)^{1 / n} \theta_{0}\).

注: 有人可能这样想: \(\theta\) 愈大, \(T_{1}=\min \left(X_{1}, \cdots, X_{n}\right)\) 也倾向于取大值. 为何不用基于 \(T_{1}\) 的检验? 理由在于: \(T_{1}\) 中所含 \(\theta\) 的信息不如 \(T\) 多,这一点可参考第四章 10 题. 进一步可以证明: 基于 \(T\) 的上述检验, 是 \(H_{0}\) 的一致最优检验. 这一点用附录 \(A\) 的方法不难证明。

从 \(f(x, \theta)\) 的图形 (见图 8) 看出: 观察值 \(X_{1}, \cdots, X_{n}\) 落在 \(\theta\) 附近的可能性大, 所以 \(T=\min \left(X_{1}, \cdots, X_{n}\right)\) 接近 \(\theta\) 且包含了 \(\theta\) 较多的信息. 显然, 当 \(\theta\) 大时, \(T\) 倾向于大. 故 \(H_{0}\) 的一个直观上合理的检验是: 当 \(T \leqslant C\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\). 为要根据水平 \(\alpha\) 决定 \(C\), 要算出 \(T\) 的分布. 这可按第二章第 22 题

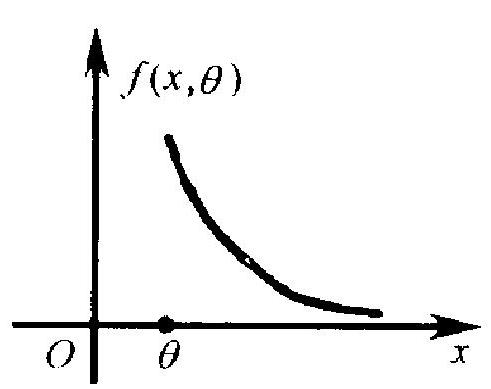
图 8 解决, 但下述观察简化了问题: 令 \(X_{i}=X_{i}-\theta, i=1, \cdots, n\). 则易见 \(X_{i}^{\prime}\) 有指数密度 \(\mathrm{e}^{-x}\) 当 \((x>0 . x \leqslant 0\) 时为 0\()\). 从此出发用第二章 22 题, 易得 \(T^{\prime}=\min \left(X_{1}^{\prime}, \cdots, X_{n}^{\prime}\right)\) 的密度函数为 \(n \mathrm{e}^{-n x}\) (当 \(x>0 . x \leqslant\) 0 时为 0\()\). 由于 \(T=T^{\prime}+\theta\), 得出 \(T\) 的密度函数 \(g(x, \theta)\) 为

\[ g(x, \theta)=\left\{\begin{array}{cl} n \mathrm{e}^{-n(x-\theta)}, & x>\theta \\ 0, & x \leqslant \theta \end{array}\right. \]

因此上述检验的功效函数为

\[ \beta(\theta)=P_{\theta}(T>C)=\int_{\max (c, \theta)}^{\infty} n \mathrm{e}^{-n(x-\theta)} \mathrm{d} x=\mathrm{e}^{-n(\max (c, \theta)-\theta)} \]

此为 \(\theta\) 的增函数 (何故?) 故为使 \(\beta(\theta) \leqslant \alpha\) 当 \(\theta \leqslant \theta_{0}\), 只须使 \(\beta\left(\theta_{0}\right)\) \(=\alpha\). 这定出 \(C=\theta_{0}+\frac{1}{n} \log \left(\frac{1}{\alpha}\right)\).

从直观上易理解应取接受域为 \(X>C, C\) 为整数. 因为 \(p\) 愈小, 为出现 \(r\) 次事件 \(A\) 所需的总试验次数就倾向于大, 上述检验的功效函数为

\[ \beta(p)=\sum_{k=0}^{c}\left(\begin{array}{c} r+k-1 \\ r-1 \end{array}\right) p^{r}(1-p)^{k} \]

需要证明它是 \(p\) 的非降函数. 这用概率方法证最容易. 如第二章习题 7 \((b)\) 的做法, 设想一个试验有三个互斥的结果 \(A_{1}, A_{2}, A_{3}\), 其概率分别为 \(p_{1}, p_{2}-p_{1}\) 和 \(1-p_{2}\). 此处 \(0 \leqslant p_{1}<p_{2} \leqslant 1\). 令 \(A=\) \(A_{1}+A_{2}\), 其概率 \(p_{2}\). 以 \(X_{1}\) 记到事件 \(A_{1}\) 出现 \(r\) 次时的试验总次数, 以 \(X_{2}\) 记到事件 \(A\) 出现 \(r\) 次时的试验总次数, 则 \(\beta\left(p_{1}\right)=\) \(P\left(X_{1}-r \leqslant C\right), \beta\left(p_{2}\right)=P\left(X_{2}-r \leqslant C\right)\). 由于总有 \(X_{1} \geqslant X_{2}\), 如 \(\left\{X_{1}-r \leqslant C\right\} \subset\left\{X_{2}-r \leqslant C\right\}\) 因而 \(\beta\left(p_{1}\right) \leqslant \beta\left(p_{2}\right)\). 这证明了 \(\beta(p)\) 的非降性. 故为使 \(\beta(p) \leqslant \alpha\) 当 \(p \leqslant p_{0}\), 只须找 \(C\), 使

\[ \beta\left(p_{0}\right)=\sum_{k=0}^{c}\left(\begin{array}{c} r+k-1 \\ r-1 \end{array}\right) p_{0}^{r}\left(1-p_{0}\right)^{k}=\alpha \]

若不存在这样的整数 \(C\), 则找 \(C\), 使

\[ \begin{gathered} \sum_{k=0}^{c}\left(\begin{array}{c} r+k-1 \\ r \end{array}\right) p_{0}^{r}\left(1-p_{0}\right)^{k}<\alpha \\ <\sum_{k=0}^{C+1}\left(\begin{array}{c} r+k-1 \\ r \end{array}\right) p_{0}^{r}\left(1-p_{0}\right)^{k} \end{gathered} \]

把上式左右两边分别记为 \(A, B\). 则准确达到水平 \(\alpha\) 的随机化检验为: 若 \(X \leqslant C\), 否定 \(H_{0}\); 若 \(X \geqslant C+2\), 接受 \(H_{0}\). 若 \(X=C+1\), 则以概率

\[ \begin{aligned} & \left(\alpha-\sum_{k=0}^{c}\left(\begin{array}{c} r+k-1 \\ r \end{array}\right) p_{0}^{r}\left(1-p_{0}\right)^{k}\right) /(B-A) \\ & =\left(\alpha-\sum_{k=0}^{c}\left(\begin{array}{c} r+k-1 \\ r \end{array}\right) p_{0}^{r}\left(1-p_{0}\right)^{k}\right) \\ & /\left[\left(\begin{array}{c} r+c \\ r \end{array}\right) p_{0}^{r}\left(1-p_{0}\right)^{c+1}\right] \end{aligned} \]

接受 \(H_{0}\).

在得到观察值 \(X\) 时, 在所述先验分布之下, \(p\) 有后验密度

\[ h(p \mid X)=\frac{1}{\beta(r+1, x+1)} p^{r}(1-p)^{x} \]

要计算积分 \(\int_{0}^{p_{0}} p^{r}(1-p)^{X} \mathrm{~d} p / \beta(r+1, X+1)\), 看是否超过 \(1 / 2\). 此积分称为“不完全 \(\beta\) 积分”, 有表可查.

因为样本 \(\left(X_{1}, \cdots, X_{n}\right)\) 的密度函数为

\[ f\left(X_{1}, \cdots, X_{n} ; \theta\right)=\theta^{-n} \text {, 当 } \max \left(X_{1}, \cdots, X_{n}\right) \equiv T \leqslant \theta \]

1. \(=0\),其他情况⚓︎

故得在所述先验分布之下, \(\left(X_{1}, \cdots, X_{n}\right)\) 的边缘密度函数为

\[ h\left(X_{1}, \cdots, X_{n}\right)=\frac{1}{a} \int_{T}^{a} \theta^{-n} \mathrm{~d} \theta=\frac{1}{(n-1) a}\left[T^{-(n-1)}-a^{-(n-1)}\right] \]

(当 \(0 \leqslant T \leqslant a\). 其他处为 0 ). 由此得 \(\theta\) 的后验密度为

\[ \begin{aligned} & h\left(\theta \mid X_{1}, \cdots, X_{n}\right) \\ & =\left\{\begin{array}{cl} (n-1) \theta^{-n} /\left(T^{-(n-1)}-a^{-(n-1)},\right. & T \leqslant \theta \leqslant a \\ 0 & , \text {, 其他处 } \end{array}\right. \end{aligned} \]

然后计算

\[ \begin{aligned} & \int_{0}^{\theta_{0}} h\left(\theta \mid X_{1}, \cdots, X_{n}\right) \mathrm{d} \theta \\ & =\left\{\begin{array}{rr} \left(T^{-(n-1)}-\theta_{0}^{-(n-1)}\right) /\left(T^{-(n-1)}-a^{-(n-1)}, \theta_{0}>T\right. \\ 0, & \theta_{0} \leqslant T \end{array}\right. \end{aligned} \]

视其值是否大于 \(1 / 2\) 而决定是否接受 \(H_{0}\).

按甲的做法, 否定域为 \(X \leqslant C, X\) 为第 9 次出现 \(A\) 时, \(\bar{A}\) 出现的次数, 其功效函数

\[ \beta_{1}(p)=P_{p}(X \leqslant C)=\sum_{k-0}^{C}\left(\begin{array}{c} 8+k \\ k \end{array}\right) p^{9}(1-p)^{k} \]

为 \(p\) 的非降函数 (第 9 题). 为定 \(C\), 应使

\[ \sum_{k=0}^{c}\left(\begin{array}{c} 8+k \\ k \end{array}\right)\left(\frac{1}{2}\right)^{9+k}=\beta_{1}(1 / 2)=0.05 \]

当 \(C=2\) 时上式为 \(0.033, C=3\) 时为 0.073 . 故如严格要求水平为 \(5 \%\), 则按第 9 题, 当 \(C=3\) (即甲的试验结果) 时, 应以概率 (0.05\(0.033) /(0.073-0.033)=0.425\) 否定 \(H_{0}\). 所以，按甲的结果, 是否接受 \(H_{0}\) 还不一定.

按乙的做法, 否定域为 \(Y>C, Y\) 为第 3 次 \(\bar{A}\) 出现时, \(A\) 出现的次数. 其功效函数为

\[ \beta_{2}(p)=P_{p}(Y>C)=1-\sum_{k=0}^{c}\left(\begin{array}{c} 2+k \\ k \end{array}\right)(1-p)^{3} p^{k} \]

此为 \(p\) 的非降函数 (何故?), 为定 \(C\), 应使

\[ 1-\sum_{k=0}^{c}\left(\begin{array}{c} 2+k \\ k \end{array}\right)\left(\frac{1}{2}\right)^{3+k}=\beta_{2}(1 / 2)=0.05 \]

当 \(C=8\) 时, 此式之值为 0.0327 . 因此, 否定域 \(\{Y>C\}\) 中的 \(C\) 值不能大于 8 . 所以, 凡是大于 8 的 \(Y\) 值, 都要否定 \(H_{0}\). 现乙的试验结果为 \(Y=9\), 故 \(H_{0}\) 必被否定.

本例有趣之处在于: 表面上甲、乙二人试验结果完全一样,都是在 12 次试验中, \(A\) 出现 9 次, \(\bar{A}\) 出现 3 次. 但由于出发点不同而导致模型有所不同, 影响了检验结果. 也有人把这类例子看成是现行统计方法的缺陷的证明, 因为他们认为: 同样的数据应导致同样的结果.

当 \(n_{1}, n_{2}\) 充分大时有 \(\left(X-n_{1} p_{1}\right) / \sqrt{n_{1} p_{1}\left(1-p_{1}\right)}-\) \(N(0,1),\left(Y-n_{2} p_{2}\right) / \sqrt{n_{2} p_{2}\left(1-p_{2}\right)} \sim N(0,1)\). 故近似地有

\[ \begin{aligned} & X / n_{1} \sim N\left(p_{1}, p_{1}\left(1-p_{1}\right) / n_{1}\right), \\ & Y / n_{2} \sim N\left(p_{2}, p_{2}\left(1-p_{2}\right) / n_{2}\right), \end{aligned} \]

因而近似地也有

\[ Z \equiv X / n_{1}-Y / n_{2}-N\left(p_{1}-p_{2}, \sigma^{2}\right) \]

其中 \(\sigma^{2}=p_{1}\left(1-p_{1}\right) / n_{1}+p_{2}\left(1-p_{2}\right) / n_{2}\). 如 \(\sigma^{2}\) 已知, 则检验 \(p_{1}-p_{2}=0\) 相当于检验正态变量 \(Z\) 之均值为 0 , 其否定域应取为 \(|Z|>\sigma u_{a / 2}\). 现 \(\sigma^{2}\) 末知, 可以用

\[ \hat{\sigma}^{2}=\hat{p}_{1}\left(1-\hat{p}_{1}\right) / n_{1}+\hat{p}_{2}\left(1-\hat{p}_{2}\right) / n_{2} \]

去估计之, \(\hat{p}_{1}=X / n_{1}, \hat{p}_{2}=Y / n_{2}\). 最后得出 \(H_{0}: p_{1}=p_{2}\) 的大样本检验的否定域为

\[ \begin{aligned} & \left|X / n_{1}-Y / n_{2}\right|>u_{a / 2}\left[\left(X / n_{1}\right)\left(1-X / n_{1}\right)\right. \\ & \left.\quad+\left(Y / n_{2}\right)\left(1-Y / n_{2}\right)\right]^{1 / 2} \end{aligned} \]

(a) 先设 \(\lambda=n, n\) 为自然数. 这时 \(X \sim P(n)\) 可表为 \(X=\) \(X_{1}+\cdots+X_{n}, X_{1}, \cdots, X_{n}\) 独立且各服从波哇松分布 \(P(1)\). 因 \(X_{i}\) 的方差为 1 , 按中心极限定理有 \(\left(X_{1}+\cdots+X_{n}-n\right) / \sqrt{n} \rightarrow N(0,1)\) 即 \((X-n) / \sqrt{n} \rightarrow N(0,1)\). 当 \(\lambda\) 不为自然数时, 设 \(n<\lambda<n+1\). 则按上面的表达式, 有 \(X_{1}+\cdots+X_{n} \leqslant X \leqslant X_{1}+\cdots+X_{n+1}\). 有

\[ \frac{X_{1}+\cdots+X_{n}-n-1}{\sqrt{\lambda}} \leqslant \frac{X-\lambda}{\sqrt{\lambda}} \leqslant \frac{X_{1}+\cdots+X_{n+1}-n}{\sqrt{\lambda}} \]

但

\[ \frac{X_{1}+\cdots+X_{n}-n-1}{\sqrt{\lambda}}=\sqrt{\frac{n}{\lambda}} \frac{X_{1}+\cdots+X_{n}-n}{\sqrt{n}}-\frac{1}{\sqrt{\lambda}} \]

因为已证 \(\left(X_{1}+\cdots+X_{n}-n\right) / \sqrt{n} \rightarrow N(0,1)\), 又 \(\sqrt{n / \lambda} \rightarrow 1\), 而 \(1 / \sqrt{\lambda} \rightarrow 0\), 知 \(\left(X_{1}+\cdots+X_{n}-n-1\right) / \sqrt{\lambda} \rightarrow N(0,1)\). 同理证明 \(\left(X_{1}+\cdots+X_{n+1}-n\right) / \sqrt{\lambda} \rightarrow N(0,1)\). 由此及 (4) 式, 即证明了 \((X-\lambda) / \sqrt{\lambda} \rightarrow N(0,1)\) 当 \(\lambda \rightarrow \infty\). (b) 否定域可取为 \(\left|X-\lambda_{0}\right| / \sqrt{\lambda_{0}}\) \(>u_{a / 2}\).

记题中之公共比值为 \(\theta\), 则易见

\[ P(X=i)=\theta^{i-1} /\left(1+\theta+\theta^{2}+\theta^{3}\right), i=1,2,3,4 \]

于是得似然函数

\[ L(\theta)=\prod_{i=1}^{4}[P(X=i)]^{n_{i}}=\theta^{n_{2}+2 n_{3}+3 n_{+}}\left(1+\theta+\theta^{2}+\theta^{3}\right)^{-n} \]

由此得到决定 \(\theta\) 值的方程 \(\mathrm{d}(\log L(\theta)) / \mathrm{d} \theta=0\), 即

\[ \left(n_{2}+2 n_{3}+3 n_{4}\right) / \theta-n\left(1+2 \theta+3 \theta^{2}\right) /\left(1+\theta+\theta^{2}+\theta^{3}\right)=0 \]

遍乘 \(\theta\left(1+\theta+\theta^{2}+\theta^{3}\right)\), 得到 \(\theta\) 的一个 3 次方程, 它有公式求解. 如有多于一个实根, 还须逐一代入 \(L(\theta)\) 中, 看哪一个达到最大, 这一个就取为 \(\theta\) 的估计值 \(\hat{\theta}\). 因只有一个参数 \(\theta\), 自由度应为 4-1 \(-1=2\).

按指数分布, 落人区间 \(I_{i}\) 内的概率为

\[ \begin{aligned} & p_{i}(\lambda)=\int_{(i-1) a}^{i a} \lambda \mathrm{e}^{-\lambda x} \mathrm{~d} x=\mathrm{e}^{-\lambda(i-1) a}\left(1-\mathrm{e}^{-\lambda a}\right), i=1, \cdots, k \\ & p_{k+1}(\lambda)=\int_{k a}^{\infty} \lambda \mathrm{e}^{-\lambda x} \mathrm{~d} x=\mathrm{e}^{-\lambda k a} \end{aligned} \]

暂记 \(\theta=\mathrm{e}^{-\lambda a}\), 得到似然函数

\[ L(\theta)=\prod_{i-1}^{k+1}\left[p_{i}(\lambda)\right]^{n_{i}}=(1-\theta)^{n-n_{k+1}} \theta^{n_{2}+2 n_{3}+\cdots+k n_{k+1}} \]

使 \(L(\theta)\) 达到最大的 \(\theta\) 为

\[ \hat{\theta}=\left(n_{2}+2 n_{3}+\cdots+k n_{k+1}\right) /\left(n_{1}+2 n_{2}+\cdots+k n_{k}+k n_{k+1}\right) \]

相应地得出 \(\lambda\) 的估计

\[ \hat{\lambda}=a^{-1} \log (1 / \hat{\theta}) \]

拟合优度统计量的自由度为 \((k+1)-1-1=k-1\).

\(1^{\circ}\) 只需注意 \(Z\) 的表达式 (3.2) 中, 当原假设成立时, 有 \(\nu_{i} \sim B\left(n, p_{i}\right)\). 故 \(E\left(n p_{i}-\nu_{i}\right)^{2}\) 就是二项分布 \(B\left(n, p_{i}\right)\) 的方差, 即 \(n p_{i}\left(1-p_{i}\right)\). 故

\[ \begin{aligned} E(Z) & =\sum_{i=1}^{k} E\left(n p_{i}-\nu_{i}\right)^{2} / n p_{i}=\sum_{i=1}^{k} n p_{i}\left(1-p_{i}\right) / n p_{i} \\ & =\sum_{i=1}^{k}\left(1-p_{i}\right)=k-\sum_{i=1}^{k} p_{i}=k-1 . \end{aligned} \]

\(2^{\circ}\) 要算 \(\operatorname{Var}(Z)\), 须计算 \(E\left(Z^{2}\right)\). 这涉及到以下两种类型的量的计算: \(E\left(n p_{1}-\nu_{1}\right)^{4}, E\left(n p_{1}-\nu_{1}\right)^{2}\left(n p_{2}-\nu_{2}\right)^{2}\). 前者较易, 它归结到 \(E\left(X^{i}\right)\) 的计算, \(X \sim B(n, p)\). 这可以利用

\[ E[X(X-1) \cdots(X-i+1) / n(n-1) \cdots(n-i+1)]=p^{i} \text { 而 } \]

得到 (第四章习题 9), 第二种类型的量归结为形如

\[ \begin{gathered} E\left[X_{1}\left(X_{1}-1\right) X_{2}\left(X_{2}-1\right)\right], E\left[X_{1}\left(X_{1}-1\right) X_{2}\right], \\ E\left(X_{1} X_{2}\right), E\left(X_{1}\right) \end{gathered} \]

等的计算, 其中 \(\left(X_{1}, X_{2}, X_{3}\right)\) 服从多项式分布 \(M\left(n ; p_{1}, p_{2}, p_{3}\right)\) (第二章例 2.2), 这可以仿照第二章例 4.1 那种方式去处理, 例如

\[ \begin{gathered} E\left[X_{1}\left(X_{1}-1\right) X_{2}\left(X_{2}-1\right)\right]=\sum^{*} \frac{n !}{i_{1} ! i_{2} !\left(n-i_{1}-i_{2}\right) !} \\ \cdot i_{1}\left(i_{1}-1\right) i_{2}\left(i_{2}-1\right) p_{1}^{i_{1}} p_{2}^{i_{2}}\left(1-p_{1}-p_{2}\right)^{n-i_{1}-i_{2}} \end{gathered} \]

\(\sum^{*}\) 表示求和范围为: \(i_{1}, i_{2}\) 为非负整数, \(i_{1}+i_{2} \leqslant n\). 上式可写为 (记 \(\left.i_{1}^{\prime}=i_{1}-2, i_{2}^{\prime}=i_{2}-2\right) \quad n(n-1)(n-2)(n-3) \times\) \(\sum^{\prime} \frac{(n-4) !}{i_{1}^{\prime} ! i_{2}^{\prime} !\left(n-4-\overline{i_{1}^{\prime}}-i_{2}^{\prime}\right) !} p_{1}^{i_{1}^{\prime}} p_{2}^{i_{2}^{\prime}}\left(1-p_{1}-p_{2}\right)^{n-4-i_{1}^{\prime}-i_{2}^{\prime}}\). \(p_{1}^{2} p_{2}^{2}, \nu^{\prime}\) 表示求和范围为: \(i_{1}^{\prime}, i_{2}^{\prime}\) 为非负整数, \(i_{1}^{\prime}+i_{2}^{\prime} \leqslant n-4\). 上式中之和为 1 . 故得

\[ E\left[X_{1}\left(X_{1}-1\right) X_{2}\left(X_{2}-1\right)\right]=n(n-1)(n-2)(n-3) p_{1}^{2} p_{2}^{2} \]

其他量类似计算,最后经过整理得到 \(Z\) 的方差(在原假设成立下) 表达式为

\[ \operatorname{Var}(Z)=2(k-1)-\left(k^{2}+2 k-2+\sum_{i=1}^{k} 1 / p_{i}\right) / n \]

其极限 (当 \(n \rightarrow \infty)\) 为 \(2(k-1)\), 即 \(\chi_{k-1}^{2}\) 的方差.

方法与附录 \(A\) 中讲的完全一样, 考虑 \(1^{\circ}\) 取定 \(p_{1}>p_{0}\), 考虑简单假设检验问题:

\[ H_{0}: p=p_{0} ; H_{1}: p=p_{1} \]

证明: (2.38)式定义的检验 \(\varphi\) 是此问题的一致最优检验. 证明这一点的方法, 按附录 \(A\), 只是归结为验证: 对否定域中的任一点 \(k\) 和接受域中的任一点 \(l\), 必有

\[ \frac{\left(\begin{array}{l} n \\ k \end{array}\right) p_{1}^{k}\left(1-p_{1}\right)^{n-k}}{\left(\begin{array}{l} n \\ k \end{array}\right) p_{0}^{k}\left(1-p_{0}\right)^{n-k}} \geqslant \frac{\left(\begin{array}{l} n \\ l \end{array}\right) p_{1}^{l}\left(1-p_{1}\right)^{n-l}}{\left(\begin{array}{l} n \\ l \end{array}\right) p_{0}^{l}\left(1-p_{0}\right)^{n-l}} \]

然后注意到检验 \(\varphi\) 与 \(p_{1}\) 无关, 且 \(\varphi\) 作为 \(p \leqslant p_{0}\) 的检验也有水平 \(\alpha\) 即可.

答案⚓︎

1. \(=0\),其他情况⚓︎

评论