练习⚓︎

设 \(X\) 为抽自正态总体 \(N\left(\theta, \sigma^{2}\right)\) 中的样本(样本大小为 1 ). \(\sigma\) 已知, \(a\), \(b\) 都是给定常数, \(a<b\). 要找原假设 \(H_{0}: a \leqslant \theta \leqslant b\) 的水平 \(\alpha\) 检验. 完成以下的步骤:

\(1^{\circ}\) 从直观考虑, \(H_{0}\) 的接受域应取为 \(C_{1} \leqslant X \leqslant C_{2}\), 即当 \(C_{1} \leqslant X \leqslant C_{2}\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\). 写出这个检验的功率函数 \(\beta(\theta)\).

\(2^{\circ}\) 找出常数 \(C_{1}, C_{2}\) 使 \(1^{\circ}\) 中找出 \(\beta(\theta)\) 满足

\[ \beta(a)=\beta(b)=\alpha \]

\(3^{\circ}\) 证明由 \(1^{\circ}, 2^{\circ}\) 决定的检验确是 \(H_{0}\) 的水平 \(\alpha\) 检验, 即 \(\beta(\theta) \leqslant \alpha\) 当 \(a \leqslant \theta\) \(\leqslant b\).

\(4^{\circ}\) 证明这样决定的检验满足

\[ \beta(\theta) \rightarrow 1 \text {, 当 }|\theta| \rightarrow \infty \]

解释这个结果的意义.

\(5^{\circ}\) 如果 \(X_{1}, \cdots, X_{n}\) 为抽自 \(N\left(\theta, \sigma^{2}\right)\) 的样本, \(\sigma\) 已知, 利用上面的结果作出 \(H_{0}\) 的检验.

设 \(X_{1}, \cdots, X_{n}\) 是抽自指数分布总体的样本, \(0<a<b, a, b\) 为已知常数. 要检验原假设 \(H_{0}: a \leqslant \lambda \leqslant b\). 描述一下 (不须详细推导) 用解第 1 题的思想来解这个问题的过程.
设 \(X_{1}, \cdots, X_{n}\) 和 \(Y_{1}, \cdots, Y_{m}\) 分别是抽自正态总体 \(N\left(a, \sigma_{1}^{2}\right)\) 和 \(N(b\), \(\left.\sigma_{2}^{2}\right)\) 的样本, \(a, b\) 末知而 \(\sigma_{1}^{2}, \sigma_{2}^{2}\) 已知. 试作出原假设 \(H_{0}: a=b\) 的水平 \(\alpha\) 检验. 给定 \(d_{1}>0, d_{2}>0\), 令 \(m=n\), 决定 \(n\), 使当 \(|a-b| \geqslant d_{1}\) 时, 功效函数不小于 \(1-d_{2}\).
设 \(X_{1}, \cdots, X_{n}\) 和 \(Y_{1}, \cdots, Y_{m}\) 分别是抽自正态总体 \(N\left(a, \sigma^{2}\right)\) 和 \(N(b\), \(\left.\sigma^{2}\right)\) 的样本, \(a, b, \sigma^{2}\) 都末知. 试仿照两样本 \(t\) 检验的做法, 构造出原假设 \(H_{0}\) : \(a=c b\) 的一个水平 \(\alpha\) 检验. 这里 \(c \neq 0\) 为已知常数.
利用上题的结果解决如下的检验问题: 设 \(X_{1}, \cdots, X_{n}\) 和 \(Y_{1}, \cdots, Y_{m}\) 分别是抽自正态总体 \(N\left(a, \sigma_{1}^{2}\right)\) 和 \(N\left(b, \sigma_{2}^{2}\right)\) 的样本, \(a, b, \sigma_{1}^{2}, \sigma_{2}^{2}\) 都末知, 但比值 \(\sigma_{2}^{2} / \sigma_{1}^{2}=c^{2}\) 已知, 要检验原假设 \(H_{0}: a=b\).
设 \(X_{1}, \cdots, X_{n}\) 为抽自具参数为 \(\lambda_{1}\) 的指数分布的样本, \(Y_{1}, \cdots, Y_{n}\) 为抽自具参数为 \(\lambda_{2}\) 的指数分布的样本. 作出原假设 \(H_{0}: \lambda_{1} \leqslant \lambda_{2}\) 的水平 \(\alpha\) 的检验.
设 \(X_{1}, \cdots, X_{n}\) 是抽自均匀分布 \(R(0, \theta)\) 的样本,给定 \(\theta_{0}>0\). 作出原假设 \(H_{0}: \theta \leqslant \theta_{0}\) 的水平 \(\alpha\) 检验.
设 \(X_{1}, \cdots, X_{n}\) 是从有下述密度函数的总体中抽出的样本;

\[ f(x, \theta)=\left\{\begin{array}{ll} \mathrm{e}^{x-\theta}, & x \leqslant \theta \\ 0, & x>\theta \end{array}-\infty<\theta<\infty\right. \]

给定常数 \(\theta_{0}\). 作出原假设 \(H_{0}: \theta \leqslant \theta_{0}\) 的水平 \(\alpha\) 检验.

注: 第 7,8 题都需要先由直观出发定出检验统计量, 再根据水平 \(\alpha\) 定临界值.

设 \(X\) 为自负二项分布

\[ P_{\theta}(X=k)=\left(\begin{array}{l} r+k-1 \\ r-1 \end{array}\right) p^{r}(1-p)^{k}, \]

\[ k=0,1,2, \cdots ; 0<\theta<1 \]

中抽出的样本. 给定 \(\theta_{0}, 0<\theta_{0}<1\). 找原假设 \(H_{0}: \theta \leqslant \theta_{0}\) 的水平 \(\alpha\) 检验. 如要求水平严格地为 \(\alpha\), 如何实行随机化?

10 . 在上题中, 如果设 \(\theta\) 有先验分布 \(R(0,1)\), 求该题中原假设 \(H_{0}\) 的贝叶斯检验.

在第 7 题中, 如果设 \(\theta\) 有先验分布 \(R(0, a)\) ( \(a\) 已知且 \(\left.a>\theta_{0}\right)\). 试求该题中原假设 \(H_{0}\) 的贝叶斯检验.
事件 \(A\) 在一试验中发生的概率记为 \(p\), 为检验原假设 \(H_{0}: p \leqslant 1 / 2\) 是否成立, 甲、乙二人分别采用下述做法: 甲重复试验到 \(A\) 第 9 次出现时停止, 乙重复试验到 \(\bar{A}\) 第 3 次出现时停止，两人都在做完第 12 次试验时, 结束试验. 取检验水平 \(\alpha=0.05\). 问: 甲乙两人分别从其试验结果中作出何种结论? 你从本题结果得到什么启发?
设样本 \(X \sim B\left(n_{1}, p_{1}\right), Y \sim B\left(n_{2}, p_{2}\right)\). 要检验假设 \(H_{0}: p_{1}=p_{2}\). 设 \(n_{1}\) 和 \(n_{2}\) 都充分大, 试作出 \(H_{0}\) 的水平 \(\alpha\) 的大样本检验.
设样本 \(X\) 服从波晆松分布 \(P(\lambda)\). (a) 试用中心极限定理证明: 当 \(\lambda\) \(\rightarrow \infty\) 时有

\[ (X-\lambda) / \sqrt{\lambda} \rightarrow N(0,1) \]

(b) 设 \(\lambda_{0}\) 充分大. 用 (a) 的结果, 作出原假设 \(H_{0}: \lambda=\lambda_{0}\) 的水平 \(\alpha\) 大样本检验.

在 5.2 节 5.2 .4 段“定数截尾”检验中, 我们定义了检验统计量 \(T\) (见(2.34)式), 并曾指出 \(2 \lambda T \sim \chi_{2}^{2} r\). 这个结果直接证明较繁, 但用下面的归纳法容易证明,试完成以下步骤。

\(1^{\circ}\) 当 \(r=1\) 时,这结果成立. 为此注意到当 \(r=1\) 时, \(T\) 就是 \(n Y_{1}\) 而 \(Y_{1}=\) \(\min \left(X_{1}, \cdots, X_{n}\right)\). 用第二章 22 题及 \(f(x)=\lambda \mathrm{e}^{-\lambda x}, x>0\), 当 \(x \leqslant 0\) 时 \(f(x)=\) 0 , 易求出 \(Y_{1}\) 之分布, 因陑求出 \(T\) 的分布. 由此算出 \(2 \lambda T\) 有密度函数 \(\frac{1}{2} \mathrm{e}^{-x / 2}\) (当 \(x>0\),下同), 此即 \(\chi^{\frac{2}{2}}\) 的密度.

\(2^{\circ}\) 设 \(r=k\) 时结果成立 (归纳假设), 要证明当 \(r=k+1\) 时结果也成立. 为此, 分别用 \(T_{k}\) 和 \(T_{k+1}\) 记当 \(r=k\) 和 \(r=k+1\) 时的 \(T\) 值, 而分析一下二者的关系, 如右图 5.6, 分别显示出 \(n\) 个元件依次失效时的寿命 \(Y_{1}, \cdots, Y_{n}\). 并为方便计,把 \(Y_{k}\) 和 \(Y_{k+1}\) 分别记为 \(a\) 和 \(b\). 从图上明显看出:

\[ T_{k+1}=T_{k}+(n-k)(b-a) \]

\(b-a\) 是什么? 就是从时刻 \(a\) 起算, 当时尚末失效的 \(n-k\) 个元件中最早失效的那个元件的失效时间 (以 \(a\) 为 0 点的时间!). 这样一来 \((n-\) \(k)(b-a)\) 不是别的,正是 \(n-k\) 个指数分布变量的最小值乘以个数 \(n-k\) (这里用了指数分布的无后效性: 当一个元件在时刻 \(a\) 尚末失效时, 其以 \(a\) 为起点以后的寿命, 仍服从原来的指数

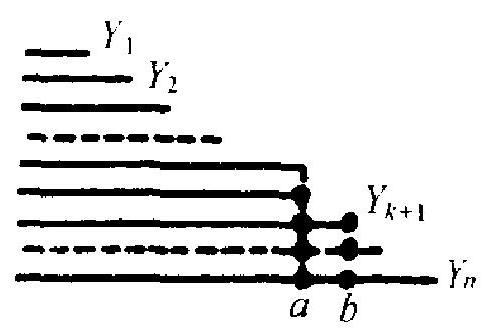
图 5.6 分布.见第二章例 1.7\()\). 根据 \(1^{\circ}\) 中已证的, \(2 \lambda(n\) \(-k)(a-b) \sim \chi_{2}^{2}\). 另外, (1) 式右边两项有独立性. 这也是根据指数分布无后效性的考惫, 而根据归纳假设, \(2 \lambda T_{k} \sim \chi_{2 k}^{2}\). 故由卡方分布性质, 知 \(2 \lambda T_{h 11}-\) \(\chi^{\frac{2}{2}}(h+1)\). 这完成了归纳证明.

这也是一种概率方法——不是单凭分析计算, 且利用概率的考虑. 它不仅简化了证明,也使我们明白了为什么有这个结果的道理所在.

设变量 \(X\) 取 \(1,2,3,4\) 等值. 有一种理论认为, \(X\) 取这 4 个值的概率呈等比级数, 即

\[ P(X=2) / P(X=1)=P(X=3) / P(X=2) \]

\[ =P(X=4) / P(X=3) \]

为验证此理论是否正确, 对 \(X\) 进行 \(n\) 次观察, 发现 \(\bar{X}\) 取 \(1,2,3,4\) 为值分别有 \(n_{1}, n_{2}, n_{3}, n_{4}\) 次. 试作拟合优度检验, 描述步骤即可以,不必去解方程.

为检验变量 \(X\) 的分布是否为指数分布 (参数 \(\lambda\) 末知), 选择适当常数 \(a>0\) 及自然数 \(k\),把区间 \([0, \infty)\) 分成 \(k+1\) 份: \(I_{1}=[0, a), I_{2}=[a, 2 a)\), \(\cdots, I_{k}=[(k-1) a, k a), I_{k+1}=[k a, \infty)\). 用 5.3 节 5.3 .4 段的方法作拟合优度检验，包括该处所介绍的估计末知参数的方法去估计 \(\lambda\). 以 \(n\) 记观察次数， \(n_{1}, n_{2}, \cdots, n_{k+1}\) 分别记这 \(n\) 个观察值中落人 \(I_{1}, I_{2}, \cdots, I_{k+1}\) 中的个数.
证明四格表的公式(3.16).
对由本章 (3.2) 式定义的拟合优度统计量 \(Z\), 我们有定理 3.1 : 在原假设下 \(Z \rightarrow \chi_{k-1}^{2}\) 当 \(n \rightarrow \infty\). 此定理末予证明,但我们可以得出若干侧证:

\(1^{\circ}\) 在原假设成立时 \(E(Z)=k-1\), 与 \(\chi_{k-1}^{2}\) 的均值一致;

\(2^{\circ}\) 在原假设成立时, \(\operatorname{Var}(Z)\) 也可以算出来, 从其表达式易看出: \(\operatorname{Var}(Z)\) \(\rightarrow 2(k-1)\) 当 \(n \rightarrow \infty\), 即收敛于 \(\chi_{k-1}^{2}\) 之方差.

\(1^{\circ}\) 很容易, 请读者证明. \(2^{\circ}\) 很繁但不难. 请读者指出计算 \(\operatorname{Var}(Z)\) 的详细步骤,如能坚持算出结果当然很好.

(此题用到附录 \(A\) 的方法)

\(1^{\circ}\) 考虑 5.2 节 5.2 .5 段的检验问题 \(1^{\circ}\). 证明: 由 (2.38) 定义的检验 \(\varphi\) (选择其中的 \(C\) 使检验水平为 \(\alpha\) ) 是水平 \(\alpha\) 的一致最优检验.

\(2^{\circ}\) 考虑 5.2 节 5.2 .6 段的检验问题 \(1^{\circ}\). 证明: 由 (2.47) 定义的检验 \(\varphi\) (选择其中的 \(C\) 使检验水平为 \(\alpha\) ) 是水平 \(\alpha\) 的一致最优检验.

练习⚓︎

评论