6.3 多元线性回归

6.3 多元线性回归

本节我们考虑有 \(p\) 个自变量 \(X_{1}, \cdots, X_{p}\) 的情形, 因变量纫记 为 \(Y\). 模型为

\[ Y=b_{0}+b_{1} X_{1}+\cdots+b_{p} X_{p}+e \]

其解释与 (2.1) 相同. 这里也有自变量为随机或非随机的区别, 今 后我们一律把自变量视为非随机的. 在 (3.1)式中, \(b_{0}\) 为常数项或 截距, \(b_{k}\) 称为 \(Y\) 对 \(X_{k}\) 的回归系数, 或称偏回归系数 \({ }^{*} . e\) 仍为随机 误差.

现设对 \(X_{1}, \cdots, X_{p}\) 和 \(Y\) 进行观察, 第 \(i\) 次观察时它们的取值 分别记为 \(X_{1 i}, \cdots, X_{p i}\) 和 \(Y_{i}\), 随机误差为 \(e_{i}\) (注意 \(e_{i}\) 不可观察), 则 得到方程

\[ Y_{i}=b_{0}+b_{1} X_{1 i}+\cdots+b_{p} X_{p i}+e_{i}, i=1, \cdots, n \]

这里假定

\[ e_{1}, \cdots, e_{n} \text { 独立同分布, } E\left(e_{i}\right)=0,0<\operatorname{Var}\left(e_{i}\right)=\sigma^{2}<\infty \]

误差方差 \(\sigma^{2}\) 末知.

统计问题仍和一元回归时一样: 要根据所得数据

\[ \left(X_{1 i}, \cdots, X_{p i}, Y_{i}\right), i=1, \cdots, n \]

对 \(b_{0}, \cdots, b_{p}\) 和误差方差 \(\sigma^{2}\) 进行估计, 对回归函数 \(b_{0}+b_{1} x_{1}+\cdots\) \(b_{p} x_{p}\) 进行估计,在自变量的给定之值 \(\left(x_{1}^{0}, \cdots, x_{p}^{0}\right)\) 处对因变量 \(Y\) 的取值进行预测, 及有关的假设检验问题等. 在上节中对一元情况 引进的不少方法和概念仍适用于此处多元的情况，但在计算和理 论方面,都较一元的情况复杂. 就本课程而言, 我们不能对这些进 行仔细的论述,只能把一些重要的结果和公式不加证明地写出来.

在讨论一元的情况时我们曾实行“中心化”, 即用 (2.6) 代替 (2.4), 这一变换对多元的情况很有用,方法也一样: 算出每个自变 量 \(X_{k}\) 在 \(n\) 次观察中取值的算术平均 \(\bar{X}_{k}=\left(X_{k 1}+\cdots+X_{k n}\right) / n\), 而 后令

\[ X_{k i}^{*}=X_{k i}-\bar{X}_{k}, i=1, \cdots, n ; k=1, \cdots, p \]

即可将 (3.2)写为

\[ Y_{i}=\beta_{0}+\beta_{1} X_{1 i}^{*}+\cdots+\beta_{p} X_{p i}^{*}+e_{i}, i=1, \cdots, n \]

• 这“偏”字的意思, 约略与微积分中偏导数中的“偏”字相当, 其真实含义是: 若只 取…自变量 \(X_{k}\) 而考虑 \(Y\) 与 \(X_{k}\) 之问的一元回归, 则回归系数 \(b_{k}^{*}\) 将与 (3.1)中的 \(b_{k}\) 不同. \(\beta_{k}\) 等与 \(b_{k}\) 等的关系是:

\[ \beta_{k}=b_{k}, k=1, \cdots, p ; \beta_{0}=b_{0}+b_{1} \bar{X}_{1}+\cdots+b_{p} \bar{X}_{p} \]

如在模型 (3.6) 之下对 \(\beta_{k}\) 等作了估计, 则可用 (3.7) 将其转化为对 \(b_{k}\) 等的估计. 在 \((3.6)\) 中有

\[ X_{k 1}^{*}+\cdots+X_{k n}^{*}=0, k=1, \cdots, p \]

以后我们只讨论 (3.6), 且为书写方便计, 略去 \(X_{k i}^{*}\) 中的“*”号, 即 仍记为 \(X_{k i}\) :

\[ Y_{i}=\beta_{0}+\beta_{1} X_{1 i}+\cdots+\beta_{p} X_{p i}+e_{i}, i=1, \cdots, n \]

记住(3.8) 中的 \(X_{k i}\) 已是经过中心化的, 与 (3.2) 中的 \(X_{k i}\) 不同.

在讨论多元线性回归时, 采用矩阵和向量的记号很方便. \(m\) 行 \(n\) 列的矩阵常用一个大字字 (如 \(X, A\) 等) 去记, 有时也记为 \(\left(a_{i j}\right), a_{i j}\) 为该矩阵的 \((i, j)\) 元, 即第 \(i\) 行第 \(j\) 列之元. 当 \(m=n\) 时 称为 \(n\) 阶方阵. \(n\) 阶方阵 \(A=\left(a_{i j}\right)\), 苻 \(a_{i j}=1\), 当 \(i=j, a_{i j}=0\) 当 \(i \neq j\), 则称为 \(n\) 阶单位阵并记为 \(I\) 或 \(I_{n}\). 方阵 \(A\) 的逆方阵 (如存 在) 记为 \(A^{-1}\). 矩阵 \(A\) 的转置矩阵将记为 \(A^{\prime}\).

向量 \(a\) 一般理解为列向量, 如

\[ a=\left(\begin{array}{c} a_{1} \\ \vdots \\ a_{k} \end{array}\right) \]

为 \(k\) 维列㣌量, \(a_{i}\) 为其第 \(i\) 个分量. \(a\) 则是行向量 \(\left(a_{1}, \cdots, a_{k}\right)\). 在 矩阵或向量运算中, 0 表示各元皆为零的矩阵或向量,有相应的维 数.

若 \(A\) 为 \(m \times n\) 预阵, \(a\) 为 \(n\) 维向量, 则按矩阵乘法定义, \(A a\) 为 \(m\) 维向量, 当 \(A\) 为 \(n\) 阶方阵, 而 \(a\) 为 \(n\) 维向量时, \(a^{\prime} A a\) 是一个 数,这形式称为二次型。一般在讨论一次型时总假定 \(A\) 为对称方 阵, 即其 \((i, j)\) 元等于其 \((j, i)\) 元, 或 \(A=A\).

0.1. 1 最小二乘估计

与一元的情形一样, 令

\[ Q\left(\alpha_{0}, \alpha_{1}, \cdots, \alpha_{p}\right)=\sum_{i=1}^{n}\left(Y_{i}-\alpha_{0}-X_{1 i} \alpha_{1}-\cdots-X_{p i} \alpha_{p}\right)^{2} \]

然后找 \(\alpha_{0}, \cdots, \alpha_{p}\) 之值, 记为 \(\hat{\beta}_{0}, \cdots, \hat{\beta}_{p}\), 使上式达到最小. \(\hat{\beta}_{i}\) 等就 是 \(\beta_{i}\) 等的最小二乘估计. 作方程

\[ \partial Q / \partial \alpha_{0}=0, \partial Q / \partial \alpha_{1}=0, \cdots, \partial Q / \partial \alpha_{p}=0 \]

升加以简单的整理, 即得

\[ \begin{gathered} n \alpha_{0}=\sum_{i=1}^{n} Y_{i}, \text { 解为 } \hat{\beta}_{0}=\bar{Y} \\ l_{11} \alpha_{1}+l_{12} \alpha_{2}+\cdots+l_{1 p} \alpha_{p}=\sum_{i=1}^{n} X_{1 i} Y_{i} \\ \cdots \cdots \cdots \cdots \\ l_{p 1} \alpha_{1}+l_{p 2} \alpha_{2}+\cdots+l_{p p} \alpha_{p}=\sum_{i=1}^{n} X_{p i} Y_{i} \end{gathered} \]

此处 \(l_{u i i^{\prime}}=\sum_{i=1}^{n} X_{u i} X_{u i}\). 若引进以下的矩阵和们量 \({ }^{*}\)

\[ \begin{gathered} X=\left(\begin{array}{cccc} X_{11} & X_{12} & \cdots & X_{1 n} \\ X_{21} & X_{22} & \cdots & X_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ X_{p 1} & X_{p 2} & \cdots & X_{p n} \end{array}\right), L=\left(\begin{array}{cccc} l_{11} & l_{12} & \cdots & l_{1 p} \\ l_{21} & l_{22} & \cdots & l_{2 p} \\ \cdots & \cdots & \cdots & \cdots \\ l_{p 1} & l_{p 2} & \cdots & l_{p p} \end{array}\right) \\ Y_{(n)}=\left(\begin{array}{c} Y_{1} \\ \vdots \\ Y_{n} \end{array}\right), \beta=\left(\begin{array}{c} \beta_{1} \\ \vdots \\ \beta_{p} \end{array}\right), \hat{\beta}=\left(\begin{array}{c} \hat{\beta}_{1} \\ \vdots \\ \hat{\beta}_{p} \end{array}\right), \alpha=\left(\begin{array}{c} \alpha_{1} \\ \vdots \\ \alpha_{p} \end{array}\right) \end{gathered} \]

则 \(L=X X^{\prime}\), 方程组 (3.10) 右边各元分别是向量 \(X Y_{(n)}\) 的相应元. 于是方程组 (3.10) 可简写为

\[ L \alpha=X Y_{(n)} \]

方程组 (3.10), 即 (3.12), 称为正则方程. 其解, 即 \(\beta\) 的最小二乘

*知阵 \(\mathrm{X}\) 称为设计矩阵, 但一般设计箍阵是指末经过中心化的, 由原来的 \(\mathrm{X}_{i j}\) 所构 成的矩阵. 估计,可表为

\[ \hat{\beta}=L^{-1} X Y_{(n)} \]

一元情况中最小二乘估计的性质, 在此也对 \({ }^{*}\) :

1. \(\hat{\beta}_{0}, \hat{\beta}\) 分别是 \(\beta_{0}\) 和 \(\beta\) 的无偏估计.

\(2 . \operatorname{Cov}\left(\hat{\beta}_{0}, \hat{\beta}_{j}\right)=0, j=1, \cdots, p\), 即 \(\hat{\beta}_{0}\) 与每个 \(\hat{\beta}_{j}\) 都不相关.

\(3 \cdot \operatorname{Var}\left(\hat{\beta}_{0}\right)=\sigma^{2} / n\); 若记

\[ C=\left(c_{i j}\right)=L^{-1} \]

则 \(\operatorname{Var}\left(\hat{\beta}_{j}\right)=c_{j j} \sigma^{2}, \operatorname{Cov}\left(\hat{\beta}_{j}, \hat{\beta}_{k}\right)=c_{j k} \sigma^{2}\). 由于这个性质, 方阵 \(L^{-1}\) 在 回归分析中有很大的重要性, 一般都需要算出来. 不然的话, 解方 程 (3.10) 可用通常的消元法更简便，而无须用(3.13).

0.2. 2 误差方差 \(\sigma^{2}\) 的估计

仍如-一元回归一样,定义残差

\[ \delta_{i}=Y_{i}-\left(\hat{\beta}_{0}+X_{1 i} \hat{\beta}_{1}+\cdots+X_{p i} \hat{\beta}_{p}\right), i=1, \cdots, n \]

及残差平方和 \(\delta_{1}^{2}+\cdots+\delta_{n}^{2}\). 可证明

\[ \hat{\sigma}^{2}=\left(\delta_{1}^{2}+\cdots+\delta_{n}^{2}\right) /(n-p-1) \]

是 \(\sigma^{2}\) 的一个无偏估计.

当随机误差服从正态分布时, 可证明 \(\sum_{i=1}^{n} \delta_{i}^{2} / \sigma^{2}\) 服从自由度 \(n-p-1\) 的 \(\chi^{2}\) 分布. 这里有 \(p+1\) 个参数 \(\beta_{01}, \beta_{1}, \cdots, \beta_{p}\) 要估计, 故 自由度减少了 \(p+1\).

对此处多元的情况,类似于 (2.23)式的结果也成立:

\[ \sum_{i=1}^{n} \delta_{i}^{2}=\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}-\left(\hat{\beta}_{1} \sum_{i=1}^{n} X_{1 i} Y_{i}+\cdots+\hat{\beta}_{p} \sum_{i=1}^{n} X_{p i} Y_{i}\right) \]

× 证明见三题 7 . 此式的方便之处在于:(3.17) 右边括号内的各项, 在列出正则方程 组 (3.10) 时已算出了, 而在估计 \(\sigma^{2}\) 时, 一般先估计 \(\beta_{j}\), 故 \(\hat{\beta}_{1}, \cdots\), \(\hat{\beta}_{p}\) 等也已算出了.

0.3. 3 区间估计与预测

在作区间估计和预测时, 要假定随机误差服从正态分布, 即要 把(3.3)加强为

\[ e_{1}, \cdots, e_{n} \text { 独立同分布, } e_{i}-N\left(0, \sigma^{2}\right), i=1, \cdots, n(3.18) \]

这时, 因 \(\hat{\beta}_{0}, \cdots, \hat{\beta}_{p}\) 都是 \(Y_{1}, \cdots, Y_{n}\) 的线性函数, 它们都服从正态 分布.

1. 回归系数 \(\beta_{j}\) 的区间估计

已知 \(E\left(\hat{\beta}_{j}\right)=\beta_{j}, \operatorname{Var}\left(\hat{\beta}_{j}\right)=c_{j j} \sigma^{2}\), 故有 \(\left(\hat{\beta}_{j}-\beta_{j}\right) /\left(\sqrt{c_{j j}} \sigma\right) \sim\) \(N(0,1)\). 以 \(\sigma\) 的估计 \(\hat{\sigma}\) 代替上式中的 \(\sigma\), 则可以证明

\[ \left(\hat{\beta}_{j}-\beta_{j}\right) /\left(\hat{\sigma} \sqrt{c_{j j}}\right) \sim t_{n-p-1} \]

与一元情况相似, 由此就可以作出 \(\beta_{j}\) 的区间估计

\[ \hat{\beta}_{j}-\hat{\sigma} \sqrt{c_{j j}} t_{n-p-1}(\alpha / 2) \leqslant \beta_{j} \leqslant \hat{\beta}_{j}+\hat{\sigma} \sqrt{c_{j j}} t_{n-p-1}(\alpha / 2) \]

置信系数为 \(1-\alpha\). 类似地作出 \(\beta_{j}\) 的置信上、下界.

1. 回归函数的区间估计

仍记问归函数为

\[ m(x)=\beta_{0}+\beta_{1}\left(x_{1}-\bar{X}_{1}\right)+\cdots+\beta_{p}\left(x_{p}-\bar{X}_{p}\right) \]

\(\bar{X}_{j}\) 的意义前已指出, 为 \(\bar{X}_{j}=\left(X_{j 1}+\cdots+X_{j n}\right) / n, x=\left(x_{1}, \cdots\right.\), \(\left.x_{p}\right)^{\prime}\).

\(m(x)\) 的点估计为

\[ \hat{m}(x)=\hat{\beta}_{0}+\hat{\beta}_{1}\left(x_{1}-\bar{X}_{1}\right)+\cdots+\hat{\beta}_{p}\left(x_{p}-\bar{X}_{p}\right) \]

其期望值为 \(m(x)\). 其方差可根据 \(\hat{\beta}_{0}, \cdots, \hat{\beta}_{p}\) 的方差与协方差算 出, 结果为

\[ \lambda^{2}(x) \sigma^{2}=\left(\frac{1}{n}+\sum_{j, k=1}^{p}\left(x_{j}-\bar{X}_{j}\right)\left(x_{k}-\bar{X}_{k}\right) c_{j k}\right) \sigma^{2} \]

于是得到 \((\hat{m}(x)-m(x)) /(\lambda(x) \sigma) \sim N(0,1)\). 以 \(\hat{\sigma}\) 代替 \(\sigma\), 得到

\[ (\hat{m}(x)-m(x)) /(\lambda(x) \hat{\sigma}) \sim t_{n-p-1} \]

由此就可作出 \(m(x)\) 的区间估计为

\[ \begin{aligned} & \hat{m}(x)-\hat{\sigma} \lambda(x) \dot{t}_{n-p-1}(\alpha / 2) \\ & \quad \leqslant m(x) \leqslant \hat{m}(x)+\hat{\sigma} \lambda(x) t_{n-p-1}(\alpha / 2) \end{aligned} \]

置信系数为 \(1-\alpha\).

在 (3.22) 式中令 \(x_{1}=\cdots=x_{p}=0\), 得到原模型 (3.2) 中的常数 项 \(b_{0}\) 的区间估计.

1. 在自变量的值 \(x_{0}=\left(x_{10}, \cdots, x_{p 0}\right)\) 处预测因变量 \(Y\) 之取值 \(y_{0}\)

作为点预测, 就用 \(\hat{m}\left(x_{0}\right)\). 其区间预测与回归函数区间估计 的差别, 就在于方差多了一个 \(\sigma^{2}\), 故只须把 (3.22) 式中的 \(\lambda(x)\) 改 为 \(\sqrt{1+\lambda^{2}\left(x_{0}\right)}\) 即可:

\[ \begin{aligned} & \hat{m}\left(x_{0}\right)-\hat{\sigma} \sqrt{1+\lambda^{2}\left(x_{0}\right)} t_{n-p-1}(\alpha / 2) \\ \leqslant & y_{0} \leqslant \hat{m}\left(x_{0}\right)+\hat{\sigma} \sqrt{1+\lambda^{2}\left(x_{0}\right)} t_{n-p-1}(\alpha / 2) \end{aligned} \]

其置信系数为 \(1-\alpha\).

0.4. 4 假设检验问题

在多元回归中, 因包含了多个回归系数, 可以考虑的假设检验 问题，比一元情况要多些. 本段仍要假设随机误差服从正态分布.

1. 单个回归系数 \(\beta_{j}\) 的检验

考虑原假设 \(H_{0}: \beta_{j}=c, c\) 为给定常数,利用 (3.19), 仿照一元 情况的处理方式, 得 \(t\) 检验:

当 \(\left|\hat{\beta}_{j}-c\right| \leqslant \hat{\sigma} \sqrt{c_{j j}} t_{n-p-1}(\alpha / 2)\) 时接受 \(H_{0}\), 不然就否定 \(H_{0}\) 类似地可考虑单边假设 \(\beta_{j} \leqslant c\) 或 \(\beta_{j} \geqslant c\) 的检验问题.

在应用上, 主要考虑的一种情况是 \(c=0\). 如果假设 \(\beta_{j}=0\) 被 接受, 则可能解释为: 自变量 \(X_{j}\) 对 \(Y\) 无影响, 因而可以从回归函 数中删去. 但这种解释要慎重. 一则是样本可能太少, 二则还有其 他原因, 见 6.3.5.

1. 全体回归系数皆为 0 的检验

即原假设为

\[ H_{0}: \beta_{1}=\beta_{2}=\cdots=\beta_{p}=0 \]

这个假设的检验常称为 “回归显著性检验”, 其意思如下: 若 (3.25) 通过了, 则有可能, 所选的自变量 \(X_{1}, \cdots, X_{p}\) 其实对因变量 \(Y\) 无 影响或影响很小. 这样, 配出的经验回归方程也就没有多大意义. 任实用上, 这有两种情况: - - 是确实 \(\beta_{1}, \cdots, \beta_{p}\) 都为 0 或很小, 这时 我们选错了自变量; 一是样本太少, 随机误差的干扰太大, 以致各 自变量的作用显示不出来. 到底是哪种情况, 当然须得对具体问题 作具体分析. 但无论如何, 如果假设 \(H_{0}\) 被接受, 则总是显示, 由数 据配出的经验回归方程不理想, 不宜迳直用于实际.

反之,若 \(H_{0}\) 被否定,则这说明了: 所选定的自变量 \(X_{1}, \cdots\), \(X_{p}\), 对因变量 \(Y\) 确有一定的影响, 并非无的放矢. 通常把这说成 回归达到了显著性, 并进而引伸解释为: 所配的回归方程成立, 可 以有效地使用了. 这样的解释还需慎重, 因为检验的结果只是告诉 我们: 所选自变量中, 至少有一部分是重要的, 但也可能尚留有并 非重要的; 尤其是, 并不能排斥遗漏了其他重要因素的可能性. 这 一切要看前期工作做得如何, 不能都委之于这个检验. 我们认为, 这个检验的基本意义是事后验证性的: 研究者在事前根据专业知 识及经验, 认为已把较重要的自变量选人了, 且在一定的误差限度 内, 认为回归函数可取为线性的. 经过试验得出数据后, 他可以通 过这个检验验证一下, 原来的考虑是否有毛病. 这时, 若 \(H_{0}\) 被否 定, 他可以合理地解释为: 数据与他事前 (试验前) 的设想并不矛 盾. 反之, 若 \(H_{0}\) 被接受, 则提醒他, 也许他事前的考虑有欠周到之 处, 值得再研究-..下. 这里所谈的实质上涉及一个选择回归自变量的问题. 在一项 大型的研究中,看来与因变量 \(Y\) 有关的因素往往很多,而在回归 方程中却只宜选进一部分关系最密切的, 选多了反而不好, 前面我 们强调专业知识和经验在处理这个问题中的作用,但这并不排斥 统计分析的作用. 实际上, 回归自变量的选择问题是回归分析中很 受重视的一个课题, 近 30 年来出现了大量的工作. 这些在本书中 无法细述了, 有兴趣的读者, 可参看陈希擩和王松桂所著《近代回 归分析》的第三章.

现在我们回到假设 (3.25) 的检验问题. 我们只能解释一下导 出检验的思想,而不能仔细证明其中所涉及的分布问题.

前面我们在原模型 (3.8)之下算出了残差平方和 (3.17), 其值 暂记为 \(R_{1}\). 现如假设 (3.25) 成立, 则无异乎说我们采纳新模型

\[ Y_{i}=\beta_{0}+e_{i}, i=1, \cdots, n \]

在此模型下也计算其残差平方和 \(R_{2}\), 结果为

\[ R_{2}=\min _{\beta_{0}} \sum_{i=1}^{n}\left(Y_{i}-\beta_{0}\right)^{2}=\sum_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2} \]

对任一模型, 残差平方和愈小, 则说明数据对它的拟合愈好. 容易 看出: 数据对模型 (3.26) 的拟合程度, 快不能优于其对 (3.8) 的拟 合程度, 因为 (3.8) 中可供选择的余地比 (3.26) 大. 但拟合程度相 差多少, 则取决于模型 (3.26) 是否正确, 即假设 (3.25) 是否成立. 若 (3.26) 正确, 则差距要小些, 否则就大些 * . 这样, \(R_{2}\) 和 \(R_{1}\) 之差 \(R_{2}-R_{1}\) 可作为假设 \(H_{0}\) 正确性的一种度量: \(R_{2}-R_{1}\) 愈小, \(H_{0}\) 愈 像是成立. 理论上可以证明: 当 \(H_{0}\) 成立时有

\[ \frac{1}{\sigma^{2}}\left(R_{2}-R_{1}\right)-\chi_{p}^{2}, R_{2}-R_{1} \text { 与 } \hat{\sigma}^{2} \text { 独立 } \]

这样,再注意当随机误差服从正态分布时有

入这是一种直观的想法, 其根据在丁: 与数据拟合最好的模型, 是在真模型附近而 不是远离它一一如果远离它(这并非不叮能), 则表示经验问盺方程 趾很人,整个分析就没有多大意义广。

\[ (n-p-1) \hat{\sigma}^{2} / \sigma^{2}-\chi^{2} \cdot p-1 \]

平是, 由 \(F\) 分布的定义, 知当原假设 \(H_{0}\) 成立时有

\[ \frac{1}{p}\left(R_{2}-R_{1}\right) / \hat{\sigma}^{2} \sim F_{p, n-p-1} \]

按 (3.27) 和 (3.17), 得

\[ R_{2}-R_{1}=\hat{\beta}_{1} \sum_{i=1}^{n} X_{1 i} Y_{i}+\cdots+\hat{\beta}_{p} \sum_{i=1}^{n} X_{p i} Y_{i} \]

于是得到 (3.25) 的 \(H_{0}\) 的下述检验法:

\[ \begin{gathered} \text { 当 } \frac{1}{p} \sum_{j=1}^{p} \hat{\beta}_{j} \sum_{i-1}^{n} X_{j i} Y_{i} / \hat{\sigma}^{2} \leqslant F_{p, n-p-1}(\alpha) \text { 时接受 } H_{0} \text {, } \\ \text { 不然就否定 } H_{0} \end{gathered} \]

检验水平为 \(\alpha\). 这个检验称为 \(H_{0}\) 的 \(F\) 检验.

1. 一部分回归系数为 0 , 即

\[ H_{0}: \beta_{1}=\cdots=\beta_{r}=0 \quad(1 \leqslant r \leqslant p) \]

检验的背景是:全体自变量按其性质分成一些组，而 \(X_{1}, \cdots\), \(X_{r}\) 是反映某方面性质的因子.(3.31) 的意义是: 这方面的因子其 实不影响因变量 \(Y\) 之值.

检验方法与(3.25) 同: 以 \(R_{3}\) 记当 (3.31) 成立时的残差平方 和, 即

\[ R_{3}=\min _{\alpha_{0}, a_{r+1}, \cdots, \alpha_{p}} \sum_{i=1}^{n}\left(Y_{i}-\alpha_{0}-X_{r+1, i} \alpha_{r+1}-\cdots-X_{p i} \alpha_{p}\right)^{2} \]

然后, 可以证明: 当随机误差服从正态分布而 \(H_{0}\) 成立时, 有

\[ \frac{1}{r}\left(R_{3}-R_{1}\right) / \hat{\sigma}^{2} \sim F_{r, n-p-1} \]

于是得到(3.31) 的下述检验法:

\[ \text { 当 } \frac{1}{r}\left(R_{3}-R_{1}\right) / \hat{\sigma}^{2} \leqslant F_{r, n-p-1}(\alpha) \text { 时接受 } H_{0} \text {, 不然就否定 } H_{0} \]

检验水平为 \(\alpha\). 这个检验通称为假设 (3.31) 的 \(F\) 检验. 称呼的来 由显然是,所用的检验统计量有 \(F\) 分布. 直接计算 \(R_{3}\) 需要在新模型

\[ Y_{i}=\beta_{0}+\beta_{r+1} X_{r+1, i}+\cdots+\beta_{p} X_{p i}+e_{i}, i=1, \cdots, n \]

之下算出 \(\beta_{0}, \beta_{r+1}, \cdots, \beta_{p}\) 的最小二乘估计 \(\beta_{0}^{*}, \beta_{r+1}^{*}, \cdots, \beta_{p}^{*} \cdot \beta_{0}^{*}\) 仍为 \(\bar{Y}\), 但 \(\beta_{r+1}^{*}, \cdots, \beta_{p}^{*}\) 已与在原模型 (3.8) 之下求出的 \(\beta_{r+1}, \cdots\), \(\beta_{p}\) 的最小二乘估计 \(\hat{\beta}_{r+1}, \cdots, \hat{\beta}_{p}\) 不同，因此涉及较多计算. 下面的 公式则只须用到原模型 (3.8) 下有关的量, 不须涉及新模型 (3.33), 因此较为简单. 为引进这公式, 把(3.11) 式却义的方阵 \(L\) 分块为

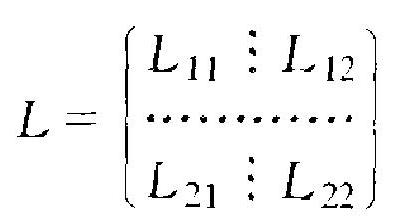
其中 \(L_{11}\) 为 \(r\) 阶方阵, 记方阵

\[ D=\left(d_{i j}\right)=L_{11}-L_{12} L_{22}^{-1} L_{21} \]

则

\[ R_{3}-R_{1}=\sum_{i, j=1}^{r} d_{i j} \hat{\beta}_{i} \hat{\beta}_{j} \]

(3.34)中, \(\hat{\beta}_{i}\) 等是在原模型 (3.8) 之下已求得的.

线性回归是统计学应用中碰得最多的. 本节方法中涉及的运 算, 早已编人各种统计软件包, 如有这种设备, 则只须输入数据即 可，这类简化公式也就没有多大实际意义了.

例 3.1 本例引述自张启锐著《实用回归分析》p. 60 . 其目的 纯粹是为了显示, 本节提出的那些抽象公式是怎样使用的.

本例共有三个自变量 \(X_{1}, X_{2}, X_{3}\), 因变量 \(Y\). 对这些变量进行 了 \(n=48\) 次观测, 原始数据 \(\left(X_{1 i}, X_{2 i}, X_{3 i}, Y_{i}\right), i=1, \cdots, 48\), 没有 写出, 但与本节公式的应用有关的量的计算结果为

\[ \begin{aligned} & \bar{X}_{1}=18.98, \bar{X}_{2}=2.55, \bar{X}_{3}=3.125, \bar{Y}=3.843 \\ & L=\left(\begin{array}{rrr} 2052.98 & 49.15 & 782.12 \\ 49.15 & 12.46 & 13.50 \\ 782.12 & 13.50 & 577.25 \end{array}\right), \sum_{i=1}^{+8}\left(Y_{i}-\bar{Y}\right)^{2}=74.15 \end{aligned} \]

\[ \begin{gathered} \sum_{i=1}^{48}\left(X_{1 i}-\bar{X}_{1}\right) Y_{i}=-257.59, \sum_{i=1}^{48}\left(X_{2 i}-\bar{X}_{2}\right) Y_{i}=-11.72, \\ \sum_{i=1}^{48}\left(X_{3 i}-\bar{X}_{3}\right) Y_{i}=-141.37 \end{gathered} \]

1. 常数项 \(\beta_{0}\) 的最小二乘估计为 \(\bar{Y}=3.843\), 而回归系数 \(\beta_{1}\), \(\beta_{2}, \beta_{3}\) 的最小二乘估计则是下述方程组的解:

\[ \begin{gathered} 2052.98 \alpha_{1}+49.15 \alpha_{2}+782.12 \alpha_{3}=-257.59 \\ 49.15 \alpha_{1}+12.46 \alpha_{2}+13.50 \alpha_{3}=-11.72 \\ 782.12 \alpha_{1}+13.50 \alpha_{2}+577.25 \alpha_{3}=-141.37 \end{gathered} \]

解 \(\alpha_{1}, \alpha_{2}, \alpha_{3}\), 即 \(\beta_{1}, \beta_{2}, \beta_{3}\) 的最小二乘估计 \(\hat{\beta}_{1}, \hat{\beta}_{2}, \hat{\beta}_{3}\), 结果为 \(\hat{\beta}_{1}\) \(=-0.0488, \hat{\beta}_{2}=-0.5688, \hat{\beta}_{3}=-0.1655\). 而经验回归方程为 \(y=3.843-0.0488\left(x_{1}-18.98\right)-0.5688\left(x_{2}-2.55\right)\)

\[ \begin{aligned} & -0.1655\left(x_{3}-3.125\right) \\ = & 6.737-0.0488 x_{1}-0.5688 x_{2}-0.1655 x_{3} \end{aligned} \]

为计算 \(\hat{\beta}_{0}, \cdots, \hat{\beta}_{3}\) 的方差协方差, 要算出 \(L\) 的逆方阵 \(C=L^{-1}\), 结 果为

\[ C=L^{-1}=10^{-3}\left(\begin{array}{rrr} 1.0931 & -2.7775 & -1.4160 \\ -2.7775 & 89.4009 & 1.6725 \\ -1.4160 & 1.6725 & 3.6119 \end{array}\right) \]

于是得到

\[ \begin{aligned} & \operatorname{Var}\left(\hat{\beta}_{0}\right)=\sigma^{2} / 48=0.0208 \sigma^{2}, \operatorname{Cov}\left(\hat{\beta}_{0}, \hat{\beta}_{j}\right)=0, j=1,2,3 \\ & \operatorname{Var}\left(\hat{\beta}_{1}\right)=10^{-3} \times 1.0931 \sigma^{2}, \operatorname{Var}\left(\hat{\beta}_{2}\right)=10^{-3} \times 89.4009 \sigma^{2} \\ & \operatorname{Var}\left(\hat{\beta}_{3}\right)=10^{-3} \times 3.6119 \sigma^{2} \\ & \operatorname{Cov}\left(\hat{\beta}_{1}, \hat{\beta}_{2}\right)=10^{-3} \times(-2.7775) \sigma^{2} \\ & \operatorname{Cov}\left(\hat{\beta}_{1}, \hat{\beta}_{3}\right)=10^{-3} \times(-1.4160) \sigma^{2} \end{aligned} \]

\(\operatorname{Cov}\left(\hat{\beta}_{2}, \hat{\beta}_{3}\right)=10^{-3} \times 3.6119 \sigma^{2}\)

1. 残差平方和按公式 (3.17) 计算, 结果为

\[ \begin{aligned} \sum_{i=1}^{18} \delta_{i}^{2}= & 74.15-(-0.0488)(-257.59) \\ & -(-0.5688)(-11.72) \\ & -(-0.1655)(-141.37) \\ = & 31.5165 \end{aligned} \]

自由度为 \(n-p-1=48-3-1=44\), 而得到误差方差 \(\sigma^{2}\) 的无偏 估计 \(\hat{\sigma}^{2}\) 为: \(\hat{\sigma}^{2}=31.5216 / 44=0.7163\).

1. 各回归系数的区间估计, 取置信系数 \(1-\alpha=0.95\), 查 \(t\) 分 布表, \(t_{4+}(0.025)=2.02108\). 于是按 \((3.20), \beta_{j}\) 的区间估计有 \(\hat{\beta}_{j} \pm\) \(\sqrt{0.7163} \times \sqrt{c_{j j}} \times 2.02108\) 的形式. 以(3.36)中的 \(c_{j j}\) 具体值代人, 算出结果为:

\[ \begin{aligned} & \beta_{1}:-0.0488 \pm 0.0564 ; \beta_{2}:-0.5688 \pm 0.5100 ; \\ & \beta_{3}:-0.1655 \pm 0.1026 \end{aligned} \]

1. 回归函数

\[ m(x)=\beta_{0}+\beta_{1}\left(x_{1}-18.98\right)+\beta_{2}\left(x_{2}-2.55\right)+\beta_{3}\left(x_{3}-\right. \]

\(3.125)\) 的区间估计, 按公式 (3.22), 应为 \(\hat{m}(x) \pm \sqrt{0.7164} \times\) \(\lambda(x) \times 2.02108\). 其中 \(\hat{m}(x)\) 即为方程 \((3.35)\) 的右边的表达式, 而

\[ \begin{aligned} \lambda^{2}(x)= & 1 / 48+\left\{1.0931\left(x_{1}-18.98\right)^{2}+89.4009\left(x_{2}-2.55\right)^{2}\right. \\ & +3.6119\left(x_{3}-3.125\right)^{2} \\ & -2 \times 2.7775\left(x_{1}-18.98\right)\left(x_{2}-2.55\right) \\ & -2 \times 1.416\left(x_{1}-18.98\right)\left(x_{3}-3.125\right) \\ & \left.+2 \times 1.6725\left(x_{2}-2.55\right)\left(x_{3}-3.125\right)\right\} \times 10^{-3} \end{aligned} \]

例如,对点 \(x=(18,2.7,3)^{\prime}\), 上式计算结果为

\[ \lambda^{2}(x)=0.02443, \hat{m}(x)=3.8263 \]

而得到其置信系数 0.95 的区间估计为

\[ \begin{gathered} 3.8263 \pm \sqrt{0.7164} \times \sqrt{0.02443} \times 2.02108 \\ =3.8163 \pm 0.2674 \end{gathered} \]

在 \(x\) 点处 \(Y\) 的预测值 \(y_{0}\) 的 0.95 置信区间为 \(\hat{m}(x) \pm \sqrt{0.7164}\) \(\left(1+\lambda^{2}(x)\right)^{12} \times 2.02108\). 在点 \(x=(18,2.7,3)^{\prime}\) 处, 结果为

\[ \begin{gathered} 3.8263 \pm \sqrt{0.7164} \times \sqrt{1.02443} \times 2.02108 \\ =3.8263 \pm 1.7314 \end{gathered} \]

看出预测的精度比回归函数估计的精度差得多.

1. 5. 假设检验

一个问归系数为 0 的检验结果 (取水平 \(\alpha=0.05\) ), 从各回归 系数的区间估计即得出: 凡是 \(\beta_{j}\) 的置信区间包含 0 者, 原假设 \(\beta_{j}\) \(=0\) 就被接受,不然就被否定. 因此, 从 (3.37) 看出, \(\beta_{1}=0\) 被接受, 而 \(\beta_{2}=0\) 及 \(\beta_{3}=0\) 都被否定.

\(\beta_{1}=0\) 虽然被接受, 但这许不等于说一定可以把自变量 \(X_{1}\) 去 掉. 这个问题还要根据具体情况全面地去考虑, 不能单华这个检验 就作出决定.

其次看原假设 \(H_{0}: \beta_{1}=0, \beta_{2}=0\). 用检验 (3.32), 要按 (3.34) 式算出 \(R_{3}-R_{1}\). 有

\[ \begin{aligned} & L_{11}=\left(\begin{array}{rr} 2052.98 & 49.15 \\ 49.15 & 12.46 \end{array}\right), L_{12}=\left(\begin{array}{r} 782.12 \\ 13.50 \end{array}\right) \\ & L_{21}=(782.12,13.50), L_{22}=(577.25) \end{aligned} \]

于是

\[ \begin{aligned} D & =L_{11}-L_{12} L_{22}^{-1} L_{21}=\left(\begin{array}{rr} 2052.98 & 49.15 \\ 49.15 & 12.46 \end{array}\right) \\ & -\left(\begin{array}{rr} 782.12 \\ 13.50 \end{array}\right)\left(\frac{1}{577.25}\right)(782.12,13.50) \\ & =\left(\begin{array}{cc} 2052.98 & 49.15 \\ 49.15 & 12.46 \end{array}\right)-\left(\begin{array}{rr} 1059.70 & 18.29 \\ 18.29 & 0.32 \end{array}\right) \\ & =\left(\begin{array}{cc} 993.18 & 30.86 \\ 30.86 & 12.14 \end{array}\right) \end{aligned} \]

f: 是, 据 \(\hat{\beta}_{1}=-0.0488, \hat{\beta}_{2}=-0.5688\), 用 \((3.34)\), 得

\[ \begin{aligned} R_{3}-R_{1}= & 993.18(0.0488)^{2}+12.14(0.5688)^{2} \\ & +2(30.86)(0.0488)(0.5688)=8.006 \end{aligned} \]

\(r=2, \hat{\sigma}^{2}=0.7164\). 故

\[ \frac{1}{r}\left(R_{3}-R_{1}\right) / \hat{\sigma}^{2}=\frac{1}{2} \times 8.006 / 0.7164=5.588 \]

查 \(F\) 分布表, 知 \(F_{r, n-p-1}(\alpha)=F_{2 .+4}(0.05) \approx 3.21\). 故 \(H_{0}\) 被否 定.

最后考虑检验问题 \(H_{0}: \beta_{1}=\beta_{2}=\beta_{3}=0\). 用检验 (3.30), 其检 验统计量之分子为

\[ \begin{gathered} \frac{1}{3}((-0.0488)(-257.59)+(-0.5688)(-11.72) \\ -(-0.1655)(-141.347))=14.211 \end{gathered} \]

故 (3.30) 中的检验统计量之值为 \(14.211 / 0.7164=19.837\).

因为 \(F_{p, n \cdots p-1}(\alpha)=F_{3,44}(0.05) \approx 2.82\), 故 \(H_{0}\) 被否定.

1.1. 5 应用上值得注意的几个问题

在一-元回归应用上所曾提出过的那些值得注意之点, 在此仍 然有效. 多元回归情况更加复杂, 在其结果的解释上更应慎重.

1. 设 \(Y\) 对自变量 \(X_{j}\) 的回归系数估计值为 \(\hat{\beta}_{j}\), 通常把它解释 为: 当 \(X_{j}\) 增减 1 单位时,平均说来因变量 \(Y\) 增减 \(\hat{\beta}_{j}\) 单位. 如果 \(X_{j}\) 的取值能由人控制, 其范围在建立经验回归方程时所用数据的范 围内, 且在尔后的使用时, 其条件与建立回归方程时的条件相当, 则这个解释可以认为是合理的.

如果 \(X_{j}\) 本身也是随机的,则情况复杂,不仅在一元情况下所 茾的那些问题此处都存在，而且还有一个各白变量之间的相关问 题. 如果自变量为随机的, 它们一般不见得独立, 即一个变量, 例如 \(\mathrm{X}_{i}\), 其值的变动往往会带动其他变量的值作变动. 这时, 各回归系 数的值, 都是在全体自变量值的联合变动的格局内起作用, 㧓立. 地 抽…个去考察就不一定很现实了. 在这种情况下, 尤其不能人为地 去设法变动其中一个 (例如 \(\left.X_{j}\right)\) 之值而强行压住其他自变量值保 持不变. 在这样人为干预下所作的预测往往与实际相去甚远.

在使用线性回归时我们必须军记一个基本点: 真实的回归函 数,特别在较大的范围内, 很少是线性的. 线性是一种近似. 它包含 了一种从实际角度看往往不…企合理的假定: 它认为各变量的作 用与其他变量取什么值无关, 月各变量的作用可以叠加. 因为, 若 \(y=b_{0}+b_{1} x_{1}+\cdots+b_{p} x_{p}\), 则不论你把 \(x_{2}, \cdots, x_{p}\) 之值固定在何 处,当 \(x_{1}\) 增减 1 单位时: \(y\) 总是增减 \(b_{1}\) 单位. 事实常不如此. 例 如, 以 \(Y\) 记某种农作物的亩产量, \(X_{1}, X_{2}, X_{3}\) 记每亩播种量, 施肥 量与耕作深度, 则 \(X_{1}\) 起的作用如何, 与 \(X_{2}, X_{3}\) 之值有关, 其他亦 然. 这种现象称为各因素之间的“交互作肘”, 如果专业知识或经验 告诉我们, 至少有一部分自变量之间有显著的交互作用存在, 则在 自变量值较大的范围内采用线性回归就不会有很好的效果. 且在 这种情况下, 单个回归系数意义的解释, 也应是基于其他变量的平 均而雷。

1. 在实际应用中, 一个回归模型内可包含为数甚多的自变 量, 其中难免有些是密切相关的. 例如, 若 \(X_{1}\) 和 \(X_{2}\) 高度线性相 关, 则 \(X_{1}\) 起的作用, 基本上可由 \(X_{2}\) 挑起来. 反之亦然. 这样, 如果 你从方程中删除自变量 \(X_{1}, X_{2}\) 中的一个, 而对剩下的 \(p-1\) 个自 变量再配出方程, 实际效果与原来的相当. 这就造成下述在假设检 验上看来矛盾的现象: “ \(\beta_{1}=0\) ” 或 “ \(\beta_{2}=0\) ” 都可以被接受,而 “ \(\beta_{1}=\) \(\beta_{2}=0\) ”则被否定.

所以, 如果自变量是随机的, 则对它们之间的相关性的了解很 重要. 这有助丁删去那些不需要的白变量, 使配出的回归方程有更. 好的稳定性, 并简化对回归方程的解释.

1. 为得出回归系数的估计值, 要解线性方程组 (3.10), 如果 系数方阵 \(L\) 的行列式 \(|L|=0\), 则方程组 (3.10) 无解. 在应用上可 能碰到这样的情况: \(|L|\) 不为 0 但很接近于 0 . 这时, 诸系数 \(l_{l i v}\) 在 计算上-..点点误差也可能导致方程组 (3.10) 的解的重大改变, 因 涧回归系数的估计值就失掉了其稳全性和可信性。

这种情况在统计上称为“复共线性”, 意指若干个自变量之间 存在着高度的线性关系，在作多元线性回归分析时，复共线性是一 个很有破坏性的东西. 凡是可能, 应极力予以避免. 如果各自变量 取值叮人为控制，自可通过适当的设计达到这一点. 如果自变量是 随机的. 通过分析其相关性并脜去若干不必要的(可由其他自变量 代替的)自变量,可能达到这一点. 如这些都不成,则不宜强行使用 最小二乘法, 可考虑用其他更富稳定性的方法取代之. 这个问题涉 及太宽,不能在此细述. 关于复共线性, 张启锐的《实用回归分析》 第六章可以参考. 关于回归系数的种种估计方法 (最小二乘法以外 的方法), 可参看陈希擩及王松桂的《近代回归分析》第四章, 及上 引张启锐的书第九章.

1.2. 6 可转化为线性回归的模型

有时,回归函数并非自变量的线性函数,但通过取用新自变 量, 可以转化为线性回归去处理. 举几个例子说明这一点.

例 3.2 设有一... 个自变量 \(X\) 和因变量 \(Y\). 如从某种理论考虑 或数据的启示, 认为回归模型有指数形式

\[ Y=b_{0}+b_{1} \mathrm{e}^{\mathrm{cX}}+e \]

其中常数 \(c\) 已知, \(b_{0}, b_{1}\) 末知, \(e\) 为随机误差. 则通过取新自变量 \(Z\) \(=\mathrm{e}^{\mathrm{c}}\) 将其转化为一元线性回归:

\[ Y=b_{0}+b_{1} Z+e \]

若在原模型下对 \((X, Y)\) 有了观测数据 \(\left(X_{1}, Y_{1}\right), \cdots,\left(X_{n}, Y_{n}\right)\), 则 等于在新模型下有了观测数据 \(\left(Z_{1}, Y_{1}\right), \cdots,\left(Z_{n}, Y_{n}\right)\), 其中 \(Z_{i}=\) \(\mathrm{e}^{\mathrm{c}}, i=1, \cdots, n\). 若 \(c\) 也末知,则这一做法失效.

例 3.3 仍设有一个自变量 \(X\) 和因变量 \(Y\), 并认为回归函数 为 \(X\) 的多项式:

\[ Y=b_{0}+b_{1} X+b_{2} X^{2}+\cdots+b_{p} X^{p}+e \]

引进 \(p\) 个新自变量 \(X_{1}, \cdots, X_{p}\), 其中 \(X_{j}=X^{j}, j=1, \cdots, p\), 则模型 (3.39)转化为有 \(p\) 个自变量 \(X_{1}, \cdots, X_{p}\) 的多元线性回归

\[ Y=b_{0}+b_{1} X_{1}+\cdots+b_{p} X_{p}+e \]

若在原模型下对 \((X, Y)\) 有了观测数据 \(\left(X_{1}, Y_{1}\right), \cdots,\left(X_{n}, Y_{n}\right)\), 则 等于在新模型 \((3.40)\) 下有了观测数据

\[ \left(X_{1 i}, \cdots, X_{p i}, Y_{i}\right), i=1, \cdots, n \]

其中 \(X_{j i}=X_{i}^{j}, j=1, \cdots, p, i=1, \cdots, n\).

(3.39)称为“多项式回归”, 是一个应用较多的回归模型. 经过 转化后的回归模型 (3.40) 成为多元的. 变换以后的自变量 \(X_{1}, \cdots\), \(X_{p}\) 之间有严格的函数关系, 这没有关系. 因为在前面讨论线性回 归时, 并没有对自变量之间可能有的关系作过任何限制.

在模型 (3.39) 之下, 假设“ \(b_{p}=0\) ”有特殊的意义, 比方说,一开 始我们较有把握认为取 2 阶多项式已够了, 但还不太放心, 希望检 验一下. 于是我们取模型 (3.39) 而令 \(p=3\). 若假设 “ \(b_{3}=0\) ” 通过 了, 则数据不与我们原先的想法 (回归取为 2 阶多项式已足) 矛盾. 否则就须调整原来的想法.

多个变元的多项式回归也一样变换. 例如, 包含两个自变量 \(X_{1}, X_{2}\) 的二次多项式回归模型

\[ Y=b_{0}+b_{1} X_{1}+b_{2} X_{2}+b_{3} X_{1}^{2}+b_{4} X_{2}^{2}+b_{5} X_{1} X_{2}+e \]

可通过采用新自变量

\[ Z_{1}=X_{1}, Z_{2}=X_{2}, Z_{3}=X_{1}^{2}, Z_{4}=X_{2}^{2}, Z_{5}=X_{1} X_{2} \]

化为多元线性模型

\[ Y=b_{0}+b_{1} Z_{1}+\cdots+b_{5} Z_{5}+e \]

在有些情况下, 不仅自变量可施行变换, 对因变量也这样做. 例如 \(X, Y\) 有回归方程 \(y=b_{0} \mathrm{e}^{b_{1} \cdot x}, b_{0}, b_{1}\) 末知, 这不是线性的, 也 不能通过自变量的变换化为线性的. 但若令 \(Z=\log Y\), 则 \(Z=\) \(\log b_{0}+b_{1} X=\beta_{0}+\beta_{1} X\left(\beta_{0}=\log b_{0}, \beta_{1}=b_{1}\right)\), 而化为线性的.

不过对因变量所作的变换, 较之对自变量所作的变换, 存在一 个理论上的问题. 即自变量的变换不改变模型中的随机误差 \(e\) 这 一项. 因此, 有关 \(e\) 的假设 (如均值为 0 , 方差非 0 有限, 或 \(e\) 服从 正态分布之类)全都保持有效, 对因变量之变换则不然. 拿本例来 说, 原模型为

\[ Y=b_{0} \mathrm{e}^{b_{1} X}+e \]

把 \(Y\) 换成 \(Z=\log Y\), 得 \(Z=\log \left(b_{0} \mathrm{e}^{b_{1} X}+e\right)\). 形式上可写为

\[ Z=b_{0}+b_{1} X+\varepsilon, \dot{\varepsilon}=\log \left(1+e b_{0}^{-1} \mathrm{e}^{-b_{1} X}\right) \]

\(\varepsilon\) 已不能满足 \(e\) 原有的条件, 其至还和 \(X\) 有关.

因此,在对因变量作变换时,我们不是拘泥于从 (3.41) 到 (3.42) 这种形式运算. 而是从头开始: 我们觉得并认定, 若取 \(Z=\) \(\log Y\) 为因变量, 则 \(X, Z\) 的回归很近似线性, 不妨就认为它有 (3.42) 的形式而 \(\varepsilon\) 满足以往对 \(e\) 施加的条件. 这有其道理可讲: 因 为反正原模型 (3.41) 中 \(e\) 的性质, 也无非是一种假定而已, 并非先 天绝对无误. 转化成 (3.42) 后, 我们末䟫不可对 \(\varepsilon\) 作出类似的假 定, 并无先天的理由认为: 对 \(\varepsilon\) 的假定一定不如对 \(e\) 的假定那样符 合事实.

更进一步, 为达到线性回归, 有时对自变量和因变量都要施加 变换, 其方法和道理与上同, 例如, 若回归方程为 \(y=b_{0} \mathrm{e}^{b_{1} / x}\), 则通 过变换 \(u=1 / x, v=\log y\), 转化为线性型 \(v=\log b_{0}+b_{1} u\).

评论

登录github的账号后，可以直接在下方评论框中输入。

如果想进行更详细的讨论(如排版、上传图片等)，选择一个反应后并点击上方的文字，进入论坛页面。