6.5 方差分析⚓︎
6.5 方差分析⚓︎
方差分析是我们多次提到过的英国大统计学家费歇尔在本世 纪 20 年代创立的. 那时他在英国一个农业试验站工作,需要进行 许多田间试验, 为分析这种试验的结果. 他发明了方差分析法. 尔 后这个方法被用于其他的领域, 尤其是工业试验数据的分析中, 取 得了很大的成功.
这里已经点明: 方差分析所针对的数据，是经过一定的“设计” 的试验的数据, 并非任何杂乱无章的数据都适于使用方差分析法 的. 说清楚一些, 为了能有效地使用方差分析法,试验在安排上必 须满足一定的要求. 在数理统计学中有一个专门分支, 叫 “试验的 设计与分析”, 就是专为讨论这个问题. 其中的“分析”, 主要是指方 差分析, 但也不限于此.
本书以其性质所限, 不可能深人地从理论上阐述这些问题,或 涉及过多细节. 这一节的目的, 只在于结合几种最简单的情况, 介 绍一下方差分析的基本思想和做法, 也顺便解释一下试验设计的 某些重要概念.
0.1. 1 单因素完全随机化设计⚓︎
假定某个农业地区原来不曾种植小麦，现在打算种植这种作 物. 各地已有过一些优良品种, 但因本地区并无种植小麦的经验, 不知道哪一个品种最适合本地区 (有最高的产量), 甚至也不知道 这些品种对本地区是否有差别. 为此进行一个田间试验. 取一大块 地将其分成形状大小都相同的 \(n\) 小块. 设供选择的品种有 \(k\) 个, 我们打算其中的 \(n_{1}\) 小块种植品种 \(1, n_{2}\) 小块种植品种 2 , 等等, \(n_{1}+n_{2}+\cdots n_{k}=n \cdot n_{1}, n_{2}, \cdots, n_{k}\) 的选取并无严格限制. 例如, 让 \(n_{1}=n_{2}=\cdots=n_{k}\) (如 \(n / k\) 为整数), 就是一种常用的选择. 当然, 也可能有某种原因使得另外的选择更好.这没有关系, 不妨碍试验 数据的分析.
分配数目定了,接着就要定出哪些小块分给哪些品种. 而这是 用随机化的方法来定, 做法如下: 取 \(n\) 张纸片, 上面分别写上数字 \(1,2, \cdots, n\). 把它混乱并放人一个盒子里, 然后一张一张地依次抽 出来. 最先抽出的 \(n_{1}\) 个号码给品种 1 , 其次抽出的 \(n_{2}\) 个号码给品 种 2 , 以此类推一一当然, 事先已把上述 \(n\) 小块地从 1 到 \(n\) 标了 号. 例如, \(n_{1}=3\). 若最先抽出的 3 张纸条上面的数字依次是 10 , 12,3 , 则品种 1 种植在标号为 3,10 和 12 这 3 小块地上.
以上就是这个简单的品种试验的设计过程. 不要看它简单, 它 却包含了由费歇尔指出的“试验设计三原则”中的两条 (另一条将 在 6.5.4 小节中解释):
- 重复. 即上述 \(n_{1}, n_{2}, \cdots, n_{k}\) 都大于 \(1:\) 每个品种不是只种 植在一个小块, 而是多个小块, 即有重复. 这样做的原因就是因为 有随机误差存在, 而只有通过重复才能对这种误差的影响作出估 计. 在本例中, 随机误差的来源, 有各小块地在条件上的差别, 有在 进行田间操作和管理上的不均匀性 (如施肥时各小块受肥总会略 有差别), 及其他可以设想和末曾注意到的种种原因.
随机误差的存在干扰了我们发现品种间差别的工作. 两品种 间如果虽有些差别，但相对于随机误差来说没有大到一定的程度， 就可能被随机误差所掩盖. 品种间由数据上显示的差别, 究竟是实 质性的还是表面的, 只有拿随机误差这把尺子去衡量才有定准. 由 此可见随机误差的影响的估计的重要性, 而重复的目的正在于此.
- 随机化. 在本试验中共有 \(n\) 个小地块. 虽然在选择哪一大 块地时我们可能已力求其各部分条件尽量均匀, 但在划分为 \(n\) 小 块后, 各块的条件总会有些差别. 如果某个品种正好分到了条件好 的那些小块, 则它可能显示出较高产量, 而这并非由于该品种优于 其他品种。
为了使小块的分配不致因为人为的因素而偏于某一或某些品 种, 我们采用前面所描述的那种随机化分配方式, 即哪些小块分配 于哪些品种完全凭机会. 这种设计之所以称为“完全随机化”, 是指 在分配小块时, 除了随机化这一原则外, 别无其他条件限制. 这是 相对于有些试验而言, 在那些试验中, 除随机化以外, 还有别的条 件限制小块的分配一只是部分地随机化.
现在可以说, 随机化这个原则在统计学中算是确立了. 在其提 出的早期, 部分地以至于今, 并非没有反对的意思. 支持随机化原 则的主要理由有二: 一是人为的选择并不能保证有好的效果, 人们 对各试验单元 (在此为各小块) 的情况往往并无充分了解, 甚至有 时了解的情况是错误的; 二是用随机化设计所取得的试验数据, 往 往有便于进行分析的统计模型.
在本例中, 影响我们感兴趣的指标一亩产量的因素只有一 个, 即种子品种. 所考志的不同的种子品种有 \(k\) 个. 每一个具体的 品种,都称为品种这个因素的一个 “水平”, 故品种这个因素一共有 \(k\) 个水平. 以此之故, 本试验称为单因素 \(k\) 水平的试验. \(n_{i}\) 称为水 平 \(i\) 的“重复度”。
如果要考虑几种不同的配方对一种工业产品质量的影响, 则 是一个以“配方”为因素的单因素试验, 有几个配方参与试验, 就有 几个水平. 如要比较几种降压药对治疗高血压的作用,则是一个以 “药品”为因素的单因素试验, 水平数就是参与试验的药品数, 等 等. 在实际问题中, 往往有若干个因素参与试验, 这时就有多因素 试验, 见本节 6.5 .3 和 6.5.5.
0.2. 2 单因素完全随机化试验的方差分析⚓︎
设问题中涉及一个因素 \(A\), 有 \(k\) 个水平, 如上例的 \(k\) 个种子 品种. 以 \(Y_{i j}\) 记第 \(i\) 个水平的第 \(j\) 个观察值. 如上例, \(Y_{i j}\) 是种植品种 \(i\) 的第 \(j\) 小块地上的亩产量. 模型为
\(a_{i}\) 表示水平 \(i\) 的理论平均值,称为水平 \(i\) 的效应. 拿上例来说, \(a_{i}\) 就是品种 \(i\) 的平均亩产量, \(e_{i j}\) 为随机误差. 假定:
因素 \(A\) 的各水平的高低优劣, 取决于其理论平均 \(a_{i}\) 的大小. 故对模型 (5.1), 我们头一个关心的事情, 就是诸 \(a_{i}\) 是否全相同. 如果是, 则表示因素 \(A\) 对所考察的指标 \(Y\) 其实无影响. 这时我们 就说因素 \(A\) 的效应不显著, 否则就说它显著. 当然, 在实际应用 中,所谓“显著”, 是指诸 \(a_{i}\) 之间的差异要大到一定的程度. 这个 “一定的程度”, 是从其实用上的意义着眼, 而“统计显著性”, 则是 与随机误差相比而言.这一点在下文的讨论中会有所体现. 我们把 所要检验的假设写为
为检验这个假设,我们作如下的分析: (5.1) 中全部 \(n=n_{1}+\) \(\cdots+n_{k}\) 个观察值各不相同. 为什么各 \(Y_{i j}\) 的值会有差异? 从模型 (5.1) 看, 不外乎两个原因:一是各 \(a_{i}\) 可能有差异. 例如, 若 \(a_{1}>a_{2}\), 这就使 \(Y_{1 j}\) 倾向于大于 \(Y_{2 j}\).二是随机误差的存在. 这一分 析启发了如下的想法:找一个衡量全部 \(Y_{i j}\) 的变异的量, 它自然地 取为 \(\left(n=n_{1}+\cdots+n_{k}\right)\)
\(S S\) 愈大, 表示 \(Y_{i j}\) 之间的差异愈大. 然后, 设法把 \(S S\) 分解为两部 分,一部分表示随机误差的影响, 记为 \(S S_{e}\); 一部分表示因素 \(A\) 的 各水平理论平均值 \(a_{1}, \cdots, a_{k}\) 之不同带 来的影响, 记为 \(S S_{A}\).
\(S S_{e}\) 这一部分可如下分析: 固定一个 \(i\), 考虑其一切观察值 \(Y_{i 1}, Y_{i 2}, \cdots, Y_{i n}\). 它们之间的差异与诸 \(a_{i}\) 之不等无关, 而可以完 全委之于随机误差. 反映 \(Y_{i 1}, \cdots, Y_{i n}\) 的差异程度的量是 \(\sum_{j=1}^{n_{i}}\left(Y_{i j}\right.\) \(\left.-\bar{Y}_{i}\right)^{2}\), 其中
\(\bar{Y}_{i}\) 是水平 \(i\) 观察值的算术平均, 它可以作为 \(a_{i}\) 的估计. 把上述平 方和对 \(i\) 相加, 得
\(S S_{A}\) 就是 \(S S\) 与 \(S S_{e}\) 之差. 可以证明
为证此式,只须把分解式
两边平方, 先固定 \(i\) 对 \(j\) 求和, 注意
然后对 \(i=1, \cdots, k\) 求和即可. 细察 \(S S_{A}\) 的表达式,这确可以用于 衡量诸 \(a_{i}\) 之间的差异程度. 因 \(\bar{Y}_{i}\) 是 \(a_{i}\) 的估计, \(a_{i}\) 之间差异愈大, \(\bar{Y}_{i}\) 之间的差异也就倾向于大, 而由 (5.7)式看出, \(S S_{A}\) 之值也会倾 向于大.
在统计学上通常把上文的 \(S S\) 称为“总平方和”, \(S S_{A}\) 称为 “因 素 \(A\) 的平方和”, \(S S_{e}\) 称为 “误差平方和”, 而分解式 \(-S S=S S_{A}+\) \(S S_{e}\) 就称为 (本模型的) “方差分析”. 名称的来由显然: 像 \(S S\), \(S S_{A}, S_{e}\) 这种表达式,都是属于样本方差那一类的形状.
从上面的分析就得到假设 (5.3) 的一个检验法: 当比值 \(\mathrm{SS}_{\mathrm{A}} / \mathrm{SS}_{e}\) 大于某一给定界限时, 否定 \(H_{0}\), 不然就接受 \(H_{0}\). 为了根 据所给的检验水平 \(\alpha\) 确定这一界限, 要假定随机误差 \(e_{i j}\) 满足正态 分布 \(N\left(0, \sigma^{2}\right)\). 可以证明,若记
则在正态假定之下且当 \(H_{0}\) 成立时, 有
据 (5.9), 即得 (5.3) 的假设 \(H_{0}\) 的检验如下: 当 \(M S_{.1} / M S_{e} \leqslant F_{k-1, n-k}(\alpha)\) 时, 接受 \(H_{0}\), 不然就否定 \(H_{0}\)
这检验称为 (5.3)的 \(F\) 检验, 名称显然来由于 (4.31).
(5.8) 式中的 \(M S_{A}\) 和 \(M S_{e}\), 分别称为因素 \(A\) 和随机误差的 “平均平方和”. 被除数 \(k-1\) 和 \(n-k\), 分别称为这两个平方和的 当由度. \(M S\) 的自由度为 \(n-k\) 比较好理解, 因按以前多次指出 的:平方和 \(\sum_{j-1}^{n_{i}}\left(Y_{i j}-\bar{Y}_{i}\right)^{2}\) 的自由度为 \(n_{i}-1\), 故对 \(i\) 求和, 得自由 度 \(\left(n_{1}-1\right)+\cdots+\left(n_{k}-1\right)=n-k . M S_{A}\) 自由度为 \(k-1\), 初一看 好像难于理解, 因为一共有 \(k\) 个平均值 \(a_{1}, \cdots, a_{k}\). 但我们重视的 是它们之间大小的比较, 因此, 不同的有关量其实只有 \(a_{2}-a_{1}\), \(a_{3}-a_{1}, \cdots, a_{k}-a_{1}\) (以 \(a_{1}\) 为基准) 等 \(k-1\) 个, 故自由度只应为 \(k-1\). 一者自由度之和为 \((n-k)+(k-1)=n-1\), 恰好是总平方 和的自由度。
在统计应用上常把上述计算列成表格,称为方差分析表
表 6.1 单因素完全随机化试验的方差分析表
| 项 月 | \(S S\) | 自由度 | \(M S\) | \(F\) 比 | 显著性 |
|---|---|---|---|---|---|
| \(A\) (例如，品种 \()\) | \(S S_{A}\) | \(k-1\) | \(M S_{A}\) | \(M S_{A} / M S_{e}\) | \(*\) * * * , 或无 |
| 误 羞 | \(S S_{e}\) | \(n-k\) | \(M S_{e}\) | - | - |
| 总 和 | \(S S\) | \(n-1\) | - | - | - |
表 6.1 中的备栏, 除显著性一栏外, 都已解释过了. 显著性一 栏是这样的: 把算出的 \(F\) 比, 即 \(M S_{\Lambda} / M S_{k}\), 与 \(F_{k-1, n-k}(0.05)=\) \(c_{1}\) 和 \(F_{k-1,{ }^{\prime}-k}(0.01)=c_{2}\) 比较. 若 \(F\) 比> \(c_{2}\), 用双星“”, 表示 \(A\) 这个因素的效应 “高度显著”, 意思是, 即使指定 \(\alpha=0.01\) 这样 的检验水平, 原假设 \((5.3)\) 也要被否定. 如果 \(c_{1}<F\) 比 \(\leqslant c_{2}\), 则用 一个星“”表示 \(A\) 的效应“显著”, 意即在 \(\alpha=0.05\) 的水平上, 原 假设 (4.25) 要被否定. 如果 \(F\) 比 \(\leqslant c_{1}\), 则不加“”（显著性一栏空 着),表示因素 \(A\) 的效应“不显著”. 当然,这里用的 \(\alpha=0.05,0.01\) 是比较通用的习惯, 并非一定要如此不可. 应用者可根据特定的需 要改用其他值, 如 \((0.05,0.10),(0.10,0.20),(0.001,0.01)\) 等.
例 5.1 设上述品种试验中, 包含有 \(k=3\) 个品种, 分别重复 \(4 、 5\) 和 3 次, 数据为 (单位: 斤/亩)
品种 \(1: 390,410,372,385\).
品种 \(2: 375,348,354,364,362\).
品种 3: \(413,383,408\).
全部 12 个数的算术平均为 380.33 . 总平方和为
其自由度为 \(12-1=11\).
3 个品种各自数据的算术平均, 分别为 \(389.25,360.60\) 和 401.33. 因此算出误差平方和为
其自由度为 \(n-k=12-3=9\).
品种平方和 \(S S_{A}\) 可由 \(S S_{A}=S S-S S_{e}\) 算出. 但为了验算, 常 单独算出, 再验证式子 \(S S=S S_{A}+S S_{e}\) 是否成立 (由于计算中取 的位数有限, 不一定严格相同). 如果不成立, 就表示计算中有错 误, 必须从头查一查. 对此例按 (4.29) 有
自由度为 \(3-1=2\). 于是
因素 \(A\) 的 \(F\) 比为
查表得 \(F_{2,9}(0.05)=4.26, F_{2,9}(0.01)=8.02\). 因 \(9.00>8.02\), 故 品种效应是高度显著的. 以上计算结果列成彷差分析表如下:
| 项 j | 11 | \(S 5\) | 自林度 | \(M S\) | \(F\) 比 | 界苦州 |
|---|---|---|---|---|---|---|
| in | 利 | 3588.05 | 2 | 1794.68 | 9.00 | \(* *\) |
| 鉄 | \(Y_{i}\) | 1686.62 | 9 | 187.40 | - | |
| irs | 利 | 5274.67 | 11 | - | - |
检验的结果表明: 不同品种的产量之间的差异, 在统计上高度显 渚。
就本例而言, 如检验的结果不显著, 则一般就不再作进一步的 分析了. 因为, 既然假设 (5.3) 被接受, 各品种的效果视作同一, 也 就没有多少好说的了. 但在实际工作中, 最好还不这么简单地下结 论. 有两点还可以考察-下:
- 各水平理论平均值的点估计 \(\bar{Y}_{1}, \cdots, \bar{Y}_{k}\) 之间的差异如何. 若这个差异没有大到有实际意义的程度, 则加强了上述结论, 即各 品科间的差异, 即使存在, 其实际意义也很有限。
- 若 \(\bar{Y}_{1}, \cdots, \bar{Y}_{k}\) 的差异, 从应用观点看, 达到了比较重要的 程度, 则原假设 (5.3) 之被接受, 是由于随机误差的影响太大. 误差 方差 \(\sigma^{2}\) 的一个无偏估计量是 \(M S_{e}\). 可以考察一下 \(\sqrt{M S_{e}}\) 之值. 若 从应用的角度看这个值太大, 则看来本试验在精度上欠理想一 这不止是 (5.3) 的检验问题, 还有下文要谈到的区间估计问题. 这 时, 如条件允许, 应考虑增大试验规模, 以及改进试验以图尽量缩 小随机误差的影响.
如果检验的结果为显著, 则等于说有充分理由相信各理论平 均值 \(a_{1}, \cdots, a_{k}\) 并不全相问。但这新不是说它们中一定没有相同 的. 如 \(k=3\) 时, 可能 \(a_{1}\) 与 \(a_{2}\) 之间差别不显著, 而它们与 \(a_{3}\) 之间 的差别鼠著. 就指定的一对 \(a_{u}, a_{i x}\) 之间的比较, 可通过求 \(a_{u}-a_{i n}\) 的区间估计，方法如下: 按(5.2) 及 \(e_{i j}\) 服从证态分布的假定, 不难 知道
\(f\) 是
记 \(\hat{\sigma}^{2}=M S_{e}, \hat{\sigma}^{2}\) 为 \(\sigma^{2}\) 的无偏估计. 以 \(\hat{\sigma}\) 代替上式中的 \(\sigma\), 可以证明
由此出发, 就得出 \(a_{u}-a_{u}\) 的䈯信系数 \(1-\alpha\) 的置信区间是
取 \(\alpha=0.05\),算出本例中各 \(a_{u}-a_{v}\) 的区间估计为
第一和第三个区间不含 0 且全在 0 的在边, 这显示 \(a_{3}\) 和 \(a_{1}\) 都在 给定的水平 \(\alpha=0.05\) 上显著地大于 \(a_{2}\). 第二个区间包含 0 . 故虽然 从点估计上看 \(a_{3}\) 大于 \(a_{1}\), 但在 0.05 的水平上达不到显著性. 所 以, 单从统计分析的角度看, 如果要在品种 \(1,2,3\) 中挑一个最好 的, 则除品种 2 外, 品种 \(1 、 3\) 都可考虑. 因为毕竟 \(a_{3}\) 的点估计大于 \(a_{1}\) 的点估计, 若无其他的特殊理由, 我们就宁肯挑品种 3 .
读者想必已注意到: 区间估计 (5.12) 与第四章中所讲的两样 本 \(t\) 区间估计基本上一致,不同之处在于: 这里误差方差 \(\sigma^{2}\) 的估 计 \(\hat{\sigma}^{2}\) 用到了全部样本, 而不只是 \(Y_{u 1}, \cdots, Y_{u n_{u}}\) 及 \(Y_{\tau \cdot 1}, \cdots, Y_{\tau m_{v}}\). 如 果品种数很多, 则涉及的相互比较非常之多. 例如, 若有 5 个品种, 则总共将涉及 \(\left(\begin{array}{l}5 \\ 2\end{array}\right)=10\) 组比较, 即有 10 个区间估计要做. 这不仅 很不方便,而睡论上也有问题. 问题在于: 虽则对…对固定的 \(u\), \(v\),置信区间 (5.12) 成立的概率为 \(1-\alpha\), 但多个区间 (每个区间的 概率为 \(1-\alpha)\) )问时成立的概率就会小于 \(1-\alpha\). 区间数愈多, 差距 愈大. 例如, 取 5 个品种, 有 10 组 \(a_{u}-a_{v}\) 要作区间估计, 若每个区 间估计的置信系数为 0.95 , 则这 10 个区间估计同时都包含所要 估计的参数的概率, 将降至 0.6 左右. 为了克服这一困难, 统计学 中引进了一种叫做“多重比较法”的方法, 它考虑到了上面指出的 那个问题. 这个内容已超出本招范围之外, 不能在此介绍了.
0.3. 3 两因素完全试验的方差分析⚓︎
一般情况下, 在一个试验中要考虑好几个对指标可能有影响 的因素.例如在…项工业试验中,影响产品质量指标 \(Y\) 的因素可 能有反应温度、反应压力、反应时问和某种催化剂的添加量. 若反 应温度有 \(k_{1}\) 个不同的可能选择, 其他三个因素分别有 \(k_{2}, k_{3}\) 和 \(k_{4}\) 种不同的选择, 则可供选择的试验组合一共有 \(k_{1} \times k_{2} \times k_{3} \times k_{4}\) 种, 而这个试验也就称为一个 \(k_{1} \times k_{2} \times k_{3} \times k_{4}\) 试验, 如果每一可 能的组合都做一次试验, 则试验称为是 “完全” 的. 若只对一部分组 合做试验, 则称为“部分实施”. 在实际应用中部分实施很常见, 因 为完全试验往往规模太大, 为条件所不允许, 且有时并无必要. 要 作部分实施, 就有一个如何去选择那些实际进行试验的组合的问 题. 这里面有很多数学和统计问题, 它们构成“试验设计”这门学科 的主要内容之一. 本节的第 6.5 .5 小节与这个内容有关.
这种试验, 不论是完全试验或部分实施, 都有一个随机化的问 题(或分区组的问题), 见 6.5 .4 小节. 如在上述工业试验中,若全 部试验要由儿个人和几台设备去做, 则因人的技术和操作水平有 差异, 设备性能优劣有差异,需要用在前面描述过的随机化方法, 把要做的试验随机地分配给这几个人和几台设备.
为书写简便计, 这里我们讨论两因素完全试验的情况. 设有两 因素 \(A, B\), 分别有 \(k, l\) 个水平 (例如 \(A\) 为品种, 有 \(k\) 个; \(B\) 为播种 量, 考虑 \(l\) 种不同的数值, 如 20 斤 /亩, 25 斤 /亩, …). A 的水平
\(-i\) 与 \(B\) 的水平 \(j\) 的组合记为 \((i, j)\), 其试验结果记为 \(Y_{i j}, i=1, \cdots\), \(k, j=1, \cdots, l\). 统计模型定为
为解释这模型, 首先把右边分成两部分: \(e_{i j}\) 为随机误差, 它包含了 末加控制的因素 ( \(A, B\) 以外的因素)及大量随机因素的影响. 假定
另一部分 \(\mu+a_{i}+b_{j}\), 它显示水平组合 \((i, j)\) 的平均效应. 它又分 解为三部分: \(\mu\) 是总平均 (一切水平组合效应的平均), 是一个基 准. \(a_{i}\) 表示由 \(A\) 的水平 \(i\) 带来的增加部分. \(a_{i}\) 愈大, 表示因素 \(A\) 的水平 \(i\) 愈好 (设指标愈大愈好), 故 \(a_{i}\) 称为因素 \(A\) 的水平 \(i\) 的效 应. \(b_{j}\) 有类似的解释. 调整 \(\mu\) 之值, 我们可以补充要求:
事实上,如(5.15)不成立, 则分别以 \(\bar{a}\) 和 \(\bar{b}\) 记各 \(a_{i}\) 的平均值和 各 \(b_{j}\) 的平均值, 把 \(\mu\) 换为 \(\mu+\bar{a}+\bar{b}, a_{i}\) 换为 \(a_{i}-\bar{a}, b_{j}\) 换成 \(b_{j}-\) \(\bar{b}\), 则 (5.13)式不变, 而 (5.15)成立.
约束条件 (5.15)给了 \(a_{i}, b_{j}\) 的意义一种更清晰的解释: \(a_{i}>0\) 表示 \(A\) 的水平 \(i\) (的效应) 在 \(A\) 的全部水平的平均效应之上, \(a_{i}<\) 0 则相反. 另外, 这个约束条件也给了 \(\mu, a_{i}\) 和 \(b_{j}\) 的一个适当的估 计法: 把 \(Y_{i j}\) 对一切 \(i, j\) 相加. 注意到 (5.15), 有
因上式右边第二项有均值 0 , 即知
是 \(\mu\) 的一个无偏估计. 其次,有
于是,记
知 \(Y_{i}\). 为 \(\mu+a_{i}\) 的一个无偏估计. 于是得到 \(a_{i}\) 的一个无偏估计为
问法得到 \(b_{j}\) 的一个无偏估计为
它们适合约束条件: \(\hat{a}_{1}+\cdots+\hat{a}_{k}=0, \hat{b}_{1}+\cdots+\hat{b}_{l}=0\).
下面要进行方差分析, 即要设法把总平方和
分解为三个部分: \(S S_{A}, S S_{B}\) 和 \(S S_{e}\), 分别表示因素 \(A, B\) 和随机误 差的影响. 这种分解的主要目的是检验假设：
和
\(H_{0 A}\) 成立表示因素 \(A\) 对指标其实无影响. 在实际问题中, 绝对无影 响的场合少见, 但如影响甚小以致被随机误差所掩盖时, 这种影响 事实上等于没有. 因此,拿 \(S S_{A}\) 和 \(S S_{e}\) 的比作为检验统计量正符 合这一想法.
所要作的分解可如下得到: 把 \(Y_{i j}-Y\).. 写为
两边平方,对 \(i, j\) 求和. 注意到
即知所有交叉积之和皆为 0 , 而得到
第- - 个平方和可以作为因素 \(A\) 的影响的衡量, 从前述 \(Y_{i} .-Y\). 作为 \(a_{i}\) 的估计可以理解. 第二个平方和同样解释. 至于第三个平 方和可作为随机误差的影响这一点, 直接看不甚明显. 可以从两个 角度去理解: 在 \(S S\) 中去掉 \(S S_{A}\) 和 \(S S_{B}\) 后, 剩余下的再没有其他系 统性因素的影响, 故只能作为 \(S S_{\ell}\). 另外, 由模型 (5.13) 及约束条 件 (5.15), 易知
这里面已毫无 \(\mu, a_{i}, b_{j}\) 的影响, 而只含随机误差.
读者可能不很满足于上面的推导, 即怎么想到把 \(Y_{i j}-Y\). 拆 成 (5.22) 式而得出 (5.23)? 对此,我们的回答是:
- 并非在任何模型中总平方和 SS 都有适当的分解,这要看 设计如何. 比方说, 如在全部 \(k l\) 个组合中少做了1 个(即有一个 \(Y_{i j}\) 末观察), 则分解式作不出来.
- 在能进行分解时, 方差分析提供了进行分解的一般方法. 使用这个一般方法也能得到 (5.23). 但是, 由于在本模型下通过 （5.22）更易实现，我们就不用这一般方法.
得到分解式 (5.23) 后, 我们就可以像单因素情况那样, 写出下 面的方差分析表:
\(S S_{A}, S S_{B}\) 自由度分别为其水平数减去 1 , 这一点与单因素情 况相同. 总和自由度为全部观察值数目 \(k l\) 减去 1 . 剩下的就是误 差平方和自由度：
\(M S\) 就是 \(S S\) 除以其自由度. 显著性的意义也与单因素的情况相 同. 如果 \(A\) 那一行的显著性位置标上了一个星号, 即表示在水平 0.05 之下原假设 \(H_{0 A}\) 被否定. 双星则相当于水平 0.01 , 称为高度 显著. 如以前曾指出过的, 0.05 和 0.01 这两个数字只是一种习 惯，不…定拘泥。 表 6.2 两因素完全试验的方差分析表
| 项 | H | \(S S\) | 自由度: | MS | F比 | 鼠著性: |
|---|---|---|---|---|---|---|
| \(\frac{1}{3}\) | \(\begin{array}{l}S S_{H} \\ S S_{H}\end{array}\) | \(\begin{array}{l}k-1 \\ l-1\end{array}\) | \(\begin{array}{l}M S_{d} \\ M S_{R}\end{array}\) | \(\begin{array}{l}M S_{A} / M S_{r} \\ M S_{H} / M S_{e}\end{array}\) | \(\begin{array}{l}\text { 加“*”, } \\ \text { “* * 或正加 }\end{array}\) | |
| 谈 | \(y_{\mathrm{F}}\) | \(S S_{e}\) | \((k-1)(l-1)\) | \(M S\), | - | - |
| 总 | 和 | SS | \(k l-1\) | _- | - | _ |
例 5.2 在一个农业试验中, 考虑 4 种不同的种子品种 \((k=\) \(4)\) 和 3 种不同的施肥方法 \((l=3)\). 试验数据为 (单位: 斤/亩):
| 施肥 \(j\) 法 | 1 | 3 | |
|---|---|---|---|
| 1 | 292 | 316 | 325 |
| 2 | 310 | 318 | 317 |
| 3 | 320 | 318 | 310 |
| 4 | 370 | 365 | 330 |
算出
列出方差分析表如下:
| 项 目 | \(S S\) | 自由度 | \(M S\) | \(F\) 比 | 显著性 |
|---|---|---|---|---|---|
| \(A\) (品种) | 3824.25 | 3 | 1274.75 | 5.246 | \(*\) |
| \(B\) (施肥法) | 162.50 | 2 | 81.25 | 0.344 | |
| 误 差 | 1458.00 | 6 | 243.00 | - | |
| 总 和 | 5444.75 | 11 | - | - |
只有品种因素达到了显著性,而“施肥方法”这个因素末达到 鼠著性. 在 \(a=0.05\) 的水平上, 没有充分证据证明: 不同的施肥法 对产量有显著的影响.
任一因素两个不同水平的效应差的区间估计，与 (5.12)相似. 此处更简单一些: 如估计的是 \(a_{u}-a_{v}\), 则 \(n_{u}=n_{v}=l\); 如估计的是 \(b_{u}-b_{v}\), 则 \(n_{u}=n_{v}=k . \hat{\sigma}\) 仍是 \(\left(M S_{e}\right)^{1 / 2}\). 当 \(k\) 或 \(l\) 较大时, 涉及的 比较为数甚多,因而也存在单因素情况下曾指出的那种问题.
应用上的一个重要问题, 是选择一个水平组合 \((i, j)\), 使其平 均产量 \(\mu+a_{i}+b_{j}\) 达到最大. 选择的方法如下: 如在本例, 因素 \(A\) 的效应显著, 则选 \(i\), 使 \(a_{i}\) 在 \(a_{1}, \cdots, a_{k}\) 中达到最大. 从统计上说, 若 \(a_{i}\) 和 \(a_{r}\) 的差异不显著(即 \(a_{i}-a_{r}\) 的区间估计包含 0 ), 则选 \(a_{r}\) 也可以. 但若无特别理由, 总是选使 \(a_{1}, \cdots, a_{k}\) 达到最大的那个 \(i\). 因素 \(B\) 的效应不显著. 故从统计上说, 选择其任一水平 \(j\) 都可以. 但一般如无特殊原因,总是选 \(j\), 使 \(b_{j}\) 在 \(b_{1}, \cdots, b_{l}\) 中达到最大. 拿 本例来说, 应选取 \(i=4, j=2\). 注意在 \(Y_{41}, Y_{42}, Y_{43}\) 中, 最大的并 非 \(Y_{42}\) 而是 \(Y_{41}\).
还有一点要注意: 在采纳模型 (5.13) 时, 我们事实上引进了一 种假定, 即两因素 \(A, B\) 对指标的效应是可以叠加的. 换一种方式 说: 因素 \(A\) 的各水平的优少比较, 与因素 \(B\) 处在哪个水平无关, 反之亦然. 更一般的情况是: \(A, B\) 两因子有“交互作用”. 这时在模 型 (5.13)中, 还要加上表示交互作用的项 \(c_{i j}\). 这时不仅统计分析 复杂化了, 尤其是分析结果的解释也复杂化了. 本书不涉及这种情 况. 在一个特定的问题中, 交互作用是否需要考虑, 在很大程度上 取决于问题的实际背景和经验. 有时, 通过试验数据的分析也可以 看出一些问题. 例如, 若误差方差 \(\sigma^{2}\) 的估计 \(M S_{e}\) 反常地大, 则有 可能是由于交互作用所致. 因为可以证明: 若交互作用确实存在而 末加考虑, 则它的影响进入随机误差而增大了 \(M S_{e}\).
0.4. 4 单因素随机区组试验的方差分析⚓︎
在本节 (6.5.1)段中, 我们讲述了费歇尔的试验设计三原则中 的两个, 即重复和随机化. 第三个原则是“分区组”, 就是我们现在 要介绍的.
为解释“区组”这个概念, 看一个简单例子. 设有一个包含 3 个 品种的试验, 每个品种重复 5 次. 于是一共要准备 15 小块形状大 小一样的田地. 这些地可能散布在一个很大的范围内, 因而各小块 的条件会存在较大的差别, 以致使试验误差加大，固然我们可以通 过完全随机化的方法保证不发生人为的系统性偏差, 但这并不能 克服由于这 15 小块的内在不均匀性而带来的误差.
因此我们考虑如下的设计,选择 5 个村子, 每个村准备 3 小块 地,条件尽可能均匀,但不同村的地块在条件上可以有较大的差 别. 由于 3 这个数字较小, 准备 3 小块相当均勺的地块, 比之准备 15 小块均匀地块, 就更容易做到。
然后我们让每个品种在每个村子里的 3 小块中各占一块,哪 个品种占哪一块由随机化决定. 这样, 我们就有一种不完全的随机 化: 每个村子中的 3 块地必须种 3 个品种, 这一条不能变 (如用完 全随机化, 有可能某个品种在某个村子里占 2 或 3 块), 但在同一 村子里则用随机化.
同一村子里的 3 小块地, 就构成一个区组. 区组的大小, 在本 例中即小块地的数目, 为 3 . 它正好等于品种这个因素的水平数.
上述设计就叫做“随机区组设计”.“随机”的含义是在每个区 组内实行随机化. 这设计的优点, 从本例中看得很清楚: 由于每个 品种在 5 个村子里各占有一块, 即使各村子之间有较大差异, 也不 会使任一品种有利或不利,因此可以缩小误差.
一般地, 区组就是一组其条件尽可能均匀的试验单元. 区组大 小, 即所含试验单元个数,等于所考察的因素的水平数 \({ }^{*}\), 因而在 每…组内, 各水平都可以实现一次且仅一次. 在区组内实行随机 化.区组的数目则没有限制, 可多可少.
含试验单元数, 比因素水平数少. 这种风组称为“不完全区组”, 其设计问题很复杂。 区组的例子很多.例如, 要比较一种产品的 4 种不同的配方, 每配方重复 5 次,一共作 20 次. 如果由 5 个人操作, 则考虑到各人 操作水平不同而带来的误差, 可让每一个人对这 4 个配方都操作 一次, 抵消人的影响. 这时, 可以迳直把每个人看作一个区组 (严格 地说, 是每人所做的那 4 个配方构成一区组); 为要比较一种病的 几种治疗方法, 要对一些患者作临床试验. 病情不同, 病人年龄、身 体条件等的不同, 会带来误差. 因此要把病人分组: 条件尽可能相 似的病人分在一组, 病人个数即治疗方法个数, 在每一组内, 每个 治疗方法施加于…个病人 (用随机化) 时, 每…组病人就构成一个 区组, 等等.
随机区组试验的统计分析,与上段讲的两因素试验完全一样, 只消把其中的一个因素看作是区组就行，例如因素 \(A\) 有 \(k\) 个水 平, 每水平做 \(l\) 次试验, 分 \(l\) 个区组 (每区组大小为 \(k\) ). 以 \(Y_{i j}\) 记因 素 \(A\) 的水平 \(i\) 在第 \(j\) 个区组内的试验值(例如,第 \(i\) 个种子品种在 第 \(j\) 个村子里那小块上的亩产量), 则有模型 (5.13), 其中 \(\mu, a_{i}, e_{j}\) 的意义同前，而 \(b_{j}\) 则称为 (第 \(j\) 个区组的) “区组效应”, 意思是第 \(j\) 个区组优于和劣于全部区组的平均的量.拿上述品种试验来说,若 某个村一田地条件特别好, 则该村子 (区组) 的 \(b_{j}\) 值就高. 这样, 表 6.2 的方差分析表, 及其计算过程, 完全适用于此处. 所不同的是 现在因素 \(B\) 解释为区组, 而 \(S S_{B}\) 则是 “区组平方和”.
由于我们所关心的只有一个因素 \(A\), 故在方差分析表 6.2 中, 我们首先感兴趣的是因素 \(A\) 的效应是否达到显著. 但区组效 应是否达到显著也有一定的意义: 它表明区组的划分是否成功（即 是否真达到了如下的要求: 区组内各试验单元很均匀,而不同区组 内的试验单元则有较大差异). 如区组效应达到显著, 则表明区组 划分至少有一定的效果, 否则就难说, 甚或可能有反效果. 这个问 题我们略多说几句. 若在 (5.13) 中去掉标志区组的那一项 \(b_{j}\), 即 当成一个完全随机化的模型去分析, 则 \(S S\) 和 \(S S_{A}\) 仍不变, 而 \(S S_{e}\) 则将成为 (5.23) 式中的 \(S S_{B}\) 与 \(S S_{e}\) 之和. 由此看出: 如果 \(M S_{B}<\) \(M S_{e}\) (指表 6.2 中的 \(M S_{e}\) ), 则在完全随机化模型之下误差方差的 估计, 反而比在随机区组设计之下为低, 再加上自由度的损失 (完 全随机化设计之下, 误差方差估计的自由度为 \(k(l-1)\), 而在随机 区组设计之下只有 \((k-1)(l-1))\), 就使 \(A\) 和 \(F\) 比要达到显著性 更难, 即: 如果因素 \(A\) 确有效应, 则当区组划分不当时, 会降低发 现这种效应的机会。
由此可见,不是在任何场合下划分区组都好.若没有足够理由 显示不同区组间确有显著差异, 则宁肯不分. 如以前提过的那个比 较 4 种配方, 由 5 个人操作的例子. 不同的人在操作技术上总多少 会有差异, 但如没有根据认为他们之间有颇大差异, 则分区组不一 定有利. 在实际工作中, 这种界限不易掌握, 这里只能作为一条一 般性的原则谈一下.
例 5.3 重新考察例 5.2 , 把 “施肥方法” 这个因子理解为区 组. 即例 (5.2.4) 中的数据, 看作为 4 个品种在 3 个村子里种植的 结果.据该例分析,品种 \(A\) 的效应在 \(\alpha=0.05\) 的水平上达到显著 (但在 \(\alpha=0.01\) 的水平上则否), 区组效应达不到显著. 更有甚者, 区组的 \(M S(81.25)\) 还小于误差的 \(M S(243.00)\), 说明在本例中分 区组没有带来什么好处.
现如果把 (5.24) 当作为一个完全随机化试验的结果,则
\(S S_{e}\) 的自由度为 \(4(3-1)=8\), 而 \(M S_{e}=1620.50 / 8=202.56 . A\) 的 \(F\) 比为 \(M S_{A} / M S_{e}=6.29\), 也超过了 \(F_{3,8}(0.05)=4.07\), 即也得出 \(A\) 的效应为显著的结论.
0.5. 5 多因素正交表设计及方差分析⚓︎
例如,若一个试验中涉及 4 个因素 \(A, B, C, D\), 分别有 \(k, l\), \(p\) 和 \(q\) 个水平, 在效应叠加 (无交互作用) 的假定下, 模型为
其意义与 (5.13) 相似. 如做全面试验, 即对
范围内的 \((i, j, u, v)\) 都观察了 \(Y_{i j w v}\), 则方差分析与模型 \((5.13)\) 相 似. 但是, 这个作法需要做 \(k l p q\) 次试验, 这往往太多了. 如果因素 数目更多,则所需试验次数大得不现实.
因此,在实用中一般只做部分实施, 即对 (5.26) 范围内的部分 \((i, j, u, v)\) 做试验. 问题在于: 这一部分不能随心所欲地取, 其取 法必须保持某种平衡性, 以达到以下两个目的:
- 模型 (5.25) 中的有关参数 \(\mu, a_{i}, b_{j}, c_{u}, d_{v}\) 等仍能得到适 当的估计.
- 总平方和 SS 仍能进行分解, 以列出像表 6.2 那样的方差 分析表.
这个问题如何解决, 其细节已远超出本课程的范围. 在这里, 我们只介绍一种叫做“正交表”的工具,它简便易用,在实用中广为 流传。
看下面这张表
表 6.3 \(L_{8}\left(4 \times 2^{4}\right)\) 正交表
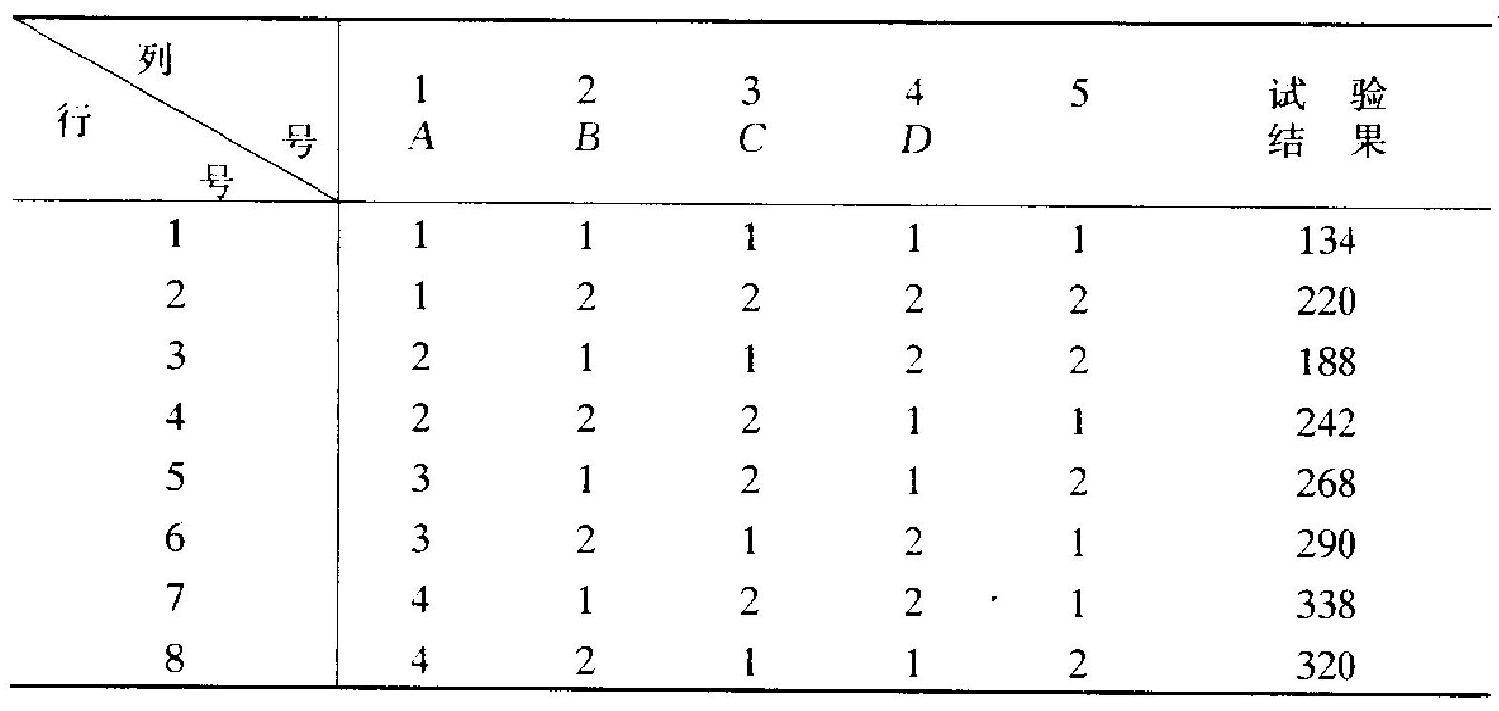
这个表一共有 8 行、5 列. 这两个数字 \((8,5)\) 有其意义: 8 表示 如用这个表安排试验, 则必须做 8 次试验, 不能多也不能少. 5 表 示最多能安排 5 个因素, 不能多, 可以少.
\(L\) 是正交表记号. \(L_{8}\) 表示表有 8 行. \(4 \times 2^{4}\) 表示: 表中有 1 列 (即第 1 列) 含有数字 \(1,2,3,4\), 有 4 列含数字 1 , 2 . 其所以称为正 交表, 是因为这表满足以下两个条件:
- 每列中含不同数字的个数一样. 例如, 第 1 列含不同数字 \(1,2,3,4\), 每种 2 个, 第 \(2-5\) 列都是含不同数字 1,2 , 每种 4 个.
- 任一列中同一数字那些位置, 在其他列中被该列所有不问 数字占据, 且个数相同. 例如, 第 3 列中数字 1 占据 \(1,3,6,8\) 行的 位置, 而在第 1 列中, 这 4 个位置恰被该列不同数字 \(1,2,3,4\) 各占 据 1 次. 在第 5 列中, 这 4 个位置则被该列不同数字 1,2 各上据 2 次。
凡是满足这两个条件的表就叫做正交表, 至于如何去构造出 这种表,那涉及许多深刻的数学问题. 实用上, 把已造出的有实用 价值的正交表汇集起来附于种种统计学著作中, 实用者按需要取 用即可.
下面来谈谈乍样利用证交表 \(L_{8}\left(4 \times 2^{-}\right)\)安排试验. 这所讲的 当然也适用于一般的正交表。归纳起来有以下几条:
- 因素的水平只能是 4 或 2 , 为 4 的至多只能有一个, 为 2 的 至多4个.
- 若试验要分区组 (例如在两台设备上做), 则区组大小只能 为 2 或 4 .
- 为确定计, 设试验中涉及 4 种配㡴 (因素 \(A\), 水平 4), 2 种 温度（因素 \(B\), 水平 2), 2 种压力 (因素 \(C\), 水平 2 ), 并分两个区组. 则配方这因子 \(A\) 必须标在第 1 列的头上, \(B 、 C\) 和区组都是 2 水 平, 可在 2-5 列中任选 3 列标上, 还有一个个空白列. 设选定表 6.3 的 1-4 列 ( \(I\) 表区组), 则设计的意义如下: 每一行读 \(A, B, C\) 所 在的三列. 例如, 第…行为 \((1,1,1)\). 这表示第 1 号试验是: \(A, B, C\) 都处在 1 水平. 第二行为 \((1,2,2)\), 表示第 2 号试验为: \(A\) 处在 1 水 平, \(B, C\) 都处在 2 水平. 第七行为 \((4,1,2)\), 表示 \(A\) 处在 4 水平, \(B\) 在 1 水平, \(C\) 在 2 水平, 等等. 区组划分则看 \(D\) 这一列. 同一数字 属于一个区组. 在这里, \(I\) 列的数字 1 在第 \(1,4,5,8\) 行, 故第 1,4 , 5,8 号试验划在一个区组内, 剩下的第 \(2,3,6,7\) 号试验划在一个 区组内。
这样…个设计必能达到表 6.3 前面提出的两条要求. 第 1 条 很容易证明, 第 2 条不能在此细证了. 考虑 (5.25), 其中 \(k=4, l=\) \(p=q=2\). 对 \(a_{i}, b_{i}, c_{u}, d_{w}\) 等也抇上约束条件(类似 (5.15)):
按 (5.25)导出上述 8 号试验的方程:
把这 8 个方程相加, 各 \(Y\) 之和记为 \(\sum Y\), 各 \(e\) 之和记为 \(\sum e\), 则 由 (5.27) 易见
由此可知 \(\bar{Y}=\sum Y / 8\) 为 \(\mu\) 的一个无偏估计.
把第 1 列为 1 处的那些 \(Y\) 相加, 得 (仍用(5.27))
由此知, \(\left(Y_{1111}+Y_{1222}\right) / 2-\bar{Y}\) 为 \(a_{1}\) 的无偏估计. 顺此以往, 对任 何 \(a_{i}, b_{j}, c_{u}, d_{\mathrm{i}}\), 都可求得其无偏估计. 例如, 要求 \(c_{2}\) 的无偏估计, 只须把 \(c\) 所在那列数字 2 对应的试验值相加, 用 (5.27), 得
于是得到 \(\left(Y_{1222}+Y_{2221}+Y_{3121}+Y_{4122}\right) / 4-\bar{Y}\) 是 \(c_{2}\) 的一个无偏 估计。
总之, 在任何一个正交裏中, 某因素水平 \(i\) 的效应 (例如本例 的 \(\left.a_{i}\right)\) 的估计, 等于该因素水平 \(i\) 的所有观察值的算术平均, 减去 全部观察值的算术平均.
接着就是计算各因素的平方和,例如 \(S S_{A}\). 如 \(A\) 有 \(k\) 个水平, 其各水平的效应 \(a_{i}\) 的估计记为 \(\hat{a}_{1}, \cdots, \hat{a}_{k}\) (其计算已如上述), 又 总试验次数为 \(n\), 则
误差平方和可以由总平方和 \(S S=\circlearrowright(Y-\bar{Y})^{2}\) 减去各因素的平. 方和求得. 其自由度等于 \(n-1\) 减去各因素的自由度一一每一因 素的自由度等于其水平数减去 1 .
例 5.4 设表 6.3 中各次试验的结果如该表右边一列所示, 我们来作出上述计算.
- 首先算出全部试验值的算术平均
及总平方和
- 估计各因素 \(A, B, C\) 各水平的效应及区组 \((D)\) 效应
这四者之和应为 0 , 这可以作为计算是否有错的一个验证. 又
- 按公式 (5.28)算出各效应及区组平方和
其自由度分别为 \(3,1,1,1\). 误差平方和为
其自由度为 \((8-1)-3-1-1-1=1\). 于是
列出方差分析表:
| 项 | H | SS | 自由度 | MS | \(F\) 比 | 显著性 |
|---|---|---|---|---|---|---|
| \(A(\) 配方) | 27272 | 3 | 9090.7 | 1136.33 | * \(\quad *\) | |
| \(B\) (滥度 \()\) | 2592 | 1 | 2592 | 324 | * | |
| \(C(\) 退力 \()\) | 2312 | 1 | 2312 | 289 | * | |
| \(D(\) 继 \()\) | 648 | 1 | 648 | 81 | ||
| 误 | 差 | 8 | 1 | 8 | - | |
| 总 | 和 | 32832 | 7 | - | - |
查 \(F\) 分布表,得
故配方这个因素的效应达到高度显著, 温度和压力这两个因素则 达到显著, 区组效应末达到显著.
某些正交表(不是所有的)也可以考虑因素间的交互作用. 这 时, 表头的安排就不能像无交互作用时那么自由, 而要受到某种规 则的限制, 具体规则由一个与该正交表配套的“交互作用表”给出. 这些都已超出本书范围, 不能在此多讲了.
评论
登录github的账号后，可以直接在下方评论框中输入。
如果想进行更详细的讨论(如排版、上传图片等)，选择一个反应后并点击上方的文字，进入论坛页面。