8.2.1 HHL 算法
线性方程是一个非常基础的概念,在人工智能和计算机科学的各个领域都会广泛应用[1]。线性方程的表达能力很强,能够用来建模刻
画并解决几乎所有的线性变化的问题,或者近似模拟很多复杂的大型系统。在回归分析中,最常使用的模型便是线性回归模型,即在对输入作初步处理后,用一个线性方程去解释现有数据,然后再对接下来出现的数据作预测。在计算机科学的其他领域中,比如数值分析,可以用线性方程求解算法来设计和分析新的算法[2]。在图论中,图上的随机游走亦可以写成一个线性约束,通过对该线性约束进行分析可以设计并且分析很多 NPC 问题的近似算法。另外,线性方程还可以用于建模计算机网络模型、天气模型、金融市场和生态模型等等。
在数学上,一个线性方程由若干个变量和关于这些变量的线性约束组成。通常,需要求解的变量用一个向量 x 表示。此时关于这些变量的线性约束就可以写成 Ax=b 的形式,其中 A 和一个矩阵,b 为另外一个向量。求解这个线性方程即求解一个 x 使得Ax=b 成立。在该问题中,输入为矩阵 A 和向量 b,输出为满足 Ax=b 的向量 x。可以看到线性方程的求解与线性代数关系密切。在经典计算机科学中,对线性代数算法的研究很多。我们知道求解一个含有 N 个变量的线性方程,至少需要的运算时间为也为 N:经典计算机至少需要逐个处理输入数据,并逐个输出解。
量子计算机在解决线性代数问题上有天然优势:得益于量子叠加态的存在,数个量子比特存在于一个指数维数的希尔伯特空间中。即一个由若干个量子比特组成的量子态就可以表示一个指数维度线性空间中的向量。同时,在该量子态上的所有量子操作亦可由线性变换表示。这使得量子态与线性空间有很简单自然的对应方式,因此,设计线性代数相关的算法也更容易。这个优势使得理论计算机科学家总是能在线性代数方向得到更优秀的算法,如矩阵求幂[3]。自然,我们也可以通过把矩阵和向量编码到量子态的方法,实现求解线性方程的更快的量子算法。然而,即使量子计算机有这个优点,仅仅依靠量子计算机从理论上并不能帮助我们更快地求出一个线性方程完整的解,
这是由于即使在量子计算机上得到一个解,这个解也是编码在一个量子态当中。由于量子态的不可复制性,对量子态进行层析得到量子态的完整信息依旧需要指数的时间复杂度。
在实际生活中,一般不会需要求解一个线性方程的整个的解,而是只需要得到解的一些性质或关于解的信息,譬如它的权重、平均值等等,这些信息往往只需要一个实数刻画。例如,在网络模型中我们不关心最终的网络流量的具体分布,只关心流量的大小,或者是在天气模型中,我们关心某种天气出现的概率等等。当不需要得到一个线性方程的完整的解此时,我们就可以利用上上述量子计算机的优点而规避其弱点而设计出更高效的算法。这是因为关于这个线性方程的解的所有信息已经在一个量子态当中,虽然无法把它完整地提取出来,但是通过对这个量子态的一次测量,我们可以得到这个量子态的部分信息。只需要根据计算目标调整最终的量子测量,用精心构造的测量就可以用很小的代价从量子态当中提取出需要的信息,而不必获得整个解,此时,由于若干个量子态可以表示指数维度的线性空间,所以可以得到指数加速。
基于以上想法,HHL 算法最早由 Harrow,Hassidim 和 Lloyd 在 2006 年提出,并以他们命名[4]。在某些条件下,该算法只需要对数时间就能将一个线性方程组的解编码到一个量子态中并进行测量以得到目标信息。设需要求解的线性方程为 Ax=b,则当 A 可逆时,解为 x=A-1b,故只需要求出 b 在 A 的逆矩阵下作用后的结果。
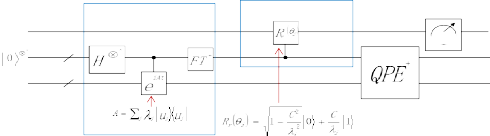
HHL 算法的基本流程为如图8-1 所示:
![]()
![]()
![]()
Phase estimation
Control rotation
![]()
![]()
![]()
图 8-1 HHL 算法的基本流程[5]
(1)首先,把 b 编码成一个量子态;
(2)应用相位估计算法,把 b 对应的量子态在A 的特征空间上作分解,并求出各特征向量对应的特征值,存储在辅助量子比特上;
(3)将各特征值求逆作用在 b 对应的量子态上;
(4)应用反向相位估计算法,清除辅助比特;
(5)此时计算的结果即是 b 在 A 的逆矩阵作用后的结果,以一个量子态的形式存在;
(6)最终通过对这个量子态作一个合适的测量,就可以得到需要的信息。
经过发展,众多改进版本的 HHL 算法被提出,表 8-1 给出了部分算法和它们的效率。
问题 | 算法 | 时间复杂度 |
LSP | CG[7] | 𝑂(𝑁𝑠𝜅 log(1/𝜖)) |
QLSP | HHL[4] | 𝑂(log(𝑁)𝑠2𝜅2/𝜖) |
QLSP | VTAA-HHL[8] | 𝑂(log(𝑁)𝑠2𝜅/𝜖) |
QLSP | Childs 等人[9] | 𝑂(𝑠𝜅𝑝𝑜𝑙𝑦𝑙𝑜𝑔(𝑠𝜅/𝜖)) |
QLSP | QLSA[10] | 𝑂(𝜅2𝑝𝑜𝑙𝑦𝑙𝑜𝑔(𝑛)‖𝐴‖𝐹/𝜖) |
表 8-1 HHL 算法及改进版本[6]
HHL 算法在量子机器学习领域有诸多应用。HHL 算法实际上实现了对数时空复杂度的矩阵求逆算法。而矩阵求逆在有监督的机器学习算法中,如支持向量机,线性回归,贝叶斯分类器等等算法中都起着决定性的作用。HHL 算法为用量子计算机加速有监督机器学习提供了算法基础[5, 11-19]。