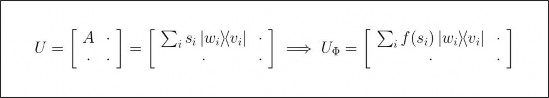
8.2.2 量子奇异值变换
量子奇异值变换(Quantum Singular Value Transformation,QVST)是近几年来量子算法领域一个突出的理论成果。该成果由 Low 和 Chuang 提出并在随后得到补充和完善[20,21]。量子奇异值变换可以视作一大类量子算法的底层逻辑,使这些算法的高效性得到理论保障,并为量子算法的设计提供了一套框架和思路。多年来许多有着广泛应用的量子算法,包括哈密顿量模拟[22]、线性系统求解器[4]、量子随机游走[23]、振幅放大算法[24]和 Grover 的搜索算法[25]等,其都可以适配到这套框架下。
大体上,量子奇异值变换主要从线性代数的角度对计算问题和量子算法进行考虑。很多具体的计算问题的输入都可以被抽象为一个矩阵,于是该计算问题就可以被描述为一个函数,该函数将矩阵映射到对应的问题输出。而量子算法的目的就是实现这一函数,或者近似地将其实现。
8.2.2.1 量子奇异值变换理论简介
接下来简单介绍量子奇异值变换的思想。前面提到问题输入可以写成矩阵的形式,假设将其记作矩阵 A。而一个量子电路可以写成一个酉方阵,假设酉方阵 U 对应了一个量子电路。如果矩阵 A 是酉方阵 U 左上角的一个子矩阵,即这一量子电路被设计来描述问题输入所包含的信息,那么就称酉方阵 U 块编码(block encode)了矩阵 A。利用块编码可以导出一些基本的算术操作。例如,假设有若干个矩阵分别被酉方阵所块编码,那么组合使用这些酉方阵对应的量子电路,
可以设计出新的量子电路对这些矩阵的凸组合进行块编码;再比如酉方阵 U 和 V 分别块编码了矩阵 A 和 B,那么可以设计出量子电路块编码矩阵 AB,即矩阵 A 和 B 的乘积。
我们知道任意矩阵都可以对其作奇异值分解。前面提到一个计算问题可以被描述为一个函数作用在问题输入对应的矩阵 A 上。如果该过程实质上能规约到将一个一元d 次多项式f 分别作用在矩阵A 的每个奇异值上。假设有量子电路即酉方阵 U,其块编码了矩阵 A。那么就可以设计出新的量子电路,其实现了上述过程,且仅使用了 d 层量子电路U。图 8-2 以公式的形式简要描述了量子奇异值变换理论的框架,其中新的量子电路如图8-3 所示。
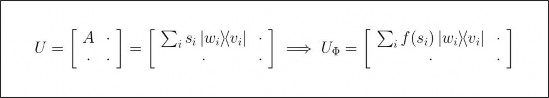
图 8-2 QVST 理论框架
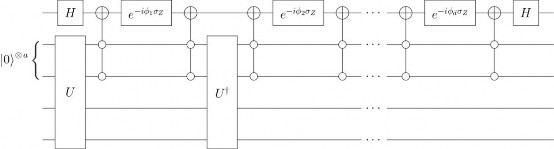
图 8-3 QVST 量子电路
举例来说,对于随机游走问题,输入矩阵即为马尔可夫链的转移矩阵P。假设有量子电路即酉方阵 U 块编码了矩阵P。为了块编码马尔可夫链上游走 t 步的转移矩阵,利用切比雪夫多项式,仅用 t 的平方根层的量子电路U 就可以近似地实现。再比如求解线性系统,问题
输入可以抽象为矩阵 A 和列向量b,问题目标是解出列向量 x,使其左乘矩阵 A 后等于列向量 b。该问题可以大致规约为求矩阵 A 的伪逆,即将倒数函数分别作用在矩阵 A 的每个奇异值上。利用多项式来近似倒数函数,就可以在量子奇异值变换的框架下,高效处理地该问题。
8.2.2.2 量子奇异值变换与量子机器学习
奇异值变换与机器学习的联系相当紧密,实现奇异值变换是一众主流机器学习算法的核心步骤之一,在量子领域同样如此。诸如量子支持向量机[11]、主成分分析[26, 27]、回归分析[4, 14, 28, 29]、慢特征分析[30]、吉布斯采样[31, 32]、玻尔兹曼机[33, 34]等,这些量子机器学习方法,都和量子奇异值变换相挂钩。许多用于解决基本的机器学习问题的量子算法,例如普通最小二乘法、加权最小二乘法、广义最小二乘法等,这些算法都可以转化到矩阵伪逆求解和矩阵乘法运算,从而能在量子奇异值变换的框架下得到高效的实现。
基于主成分分析,在量子奇异值变换的框架下,可以得到高效实现主成分回归的量子算法。主成分分析这套技术主要做的是通过剔除模型中的低相关度的特征来进行降维。该技术对数据集进行奇异值分解,或对数据集的协方差矩阵进行特征分解,由于协方差矩阵中较大的特征值对应的特征向量会指向方差较大的方向,故可以以此来判断哪些方向的特征与模型的相关度低。该技术在异常检测、量化金融等领域有着广泛应用。在对数据集做出适当假设、提供适当的黑盒运算的前提下,量子算法可以有效加速主成分分析的过程[26, 35]。
不同于主成分分析中简单地截取协方差矩阵中较小的特征值对应的部分,主成分回归会在数据集中较大的奇异值对应的数据子空间中重构目标向量。运用量子奇异值变换这一方法,可以在数据子空间中找到目标向量的最小二乘估计。相比一般的主成分分析,主成分回归运用起来更灵活也更有效。
另外,在慢特征分析的量子算法中,也有“将问题输入投影到小于特定阈值的奇异值对应的子空间”的操作,这同样可以适配到量子奇异值变换的框架中,比如将奇异值变换函数 f 设为阈值函数,或近似阈值函数的多项式。
总而言之,在机器学习方法中会用到大量矩阵分析的内容。而奇 异值分解作为矩阵分析中通用且有效的工具,被广泛应用于数据降维、矩阵压缩、图像处理和推荐系统等任务。另一方面,从线性代数的角 度对量子理论的研究由来已久,在矩阵问题的量子算法分析上也有着 广泛的理论基础。综合看来,量子奇异值变换的框架势必能在机器学 习中得到广泛的应用,亟待研究人员的发掘。