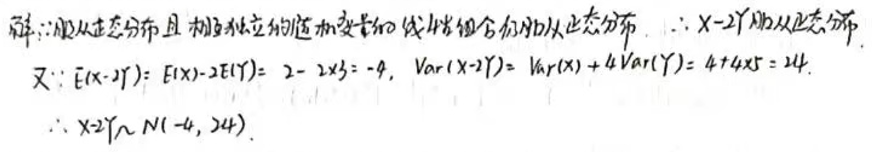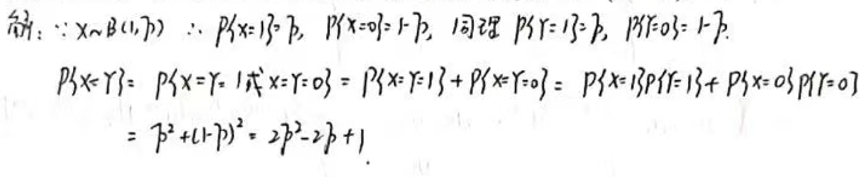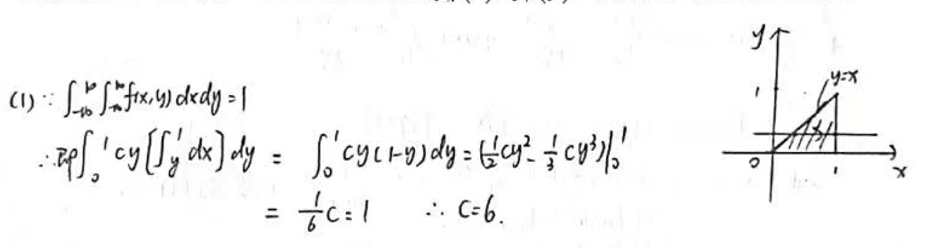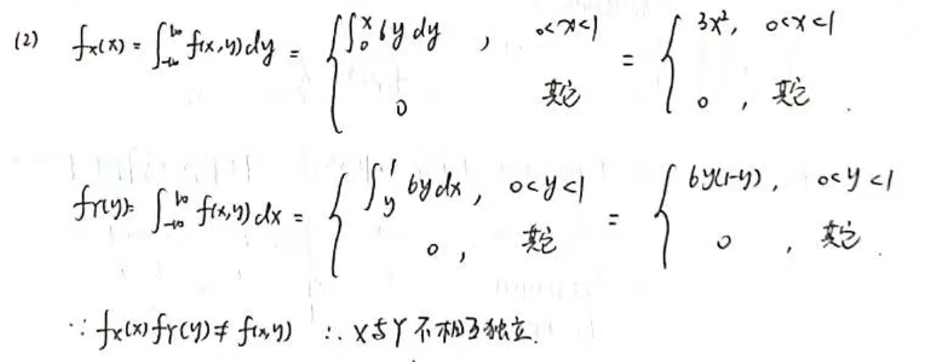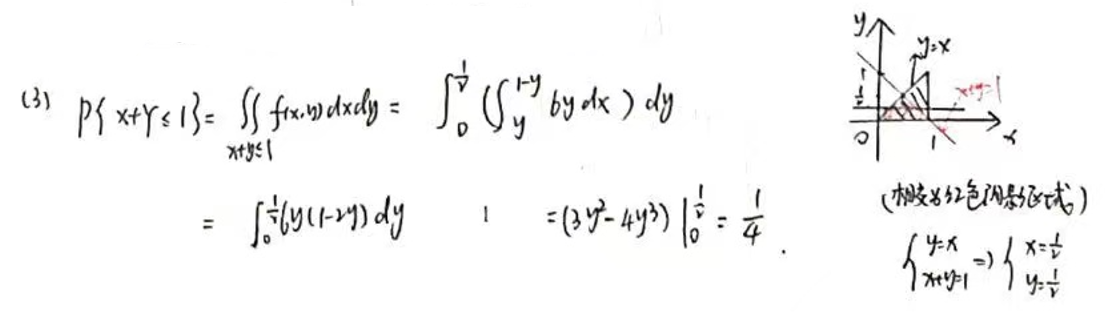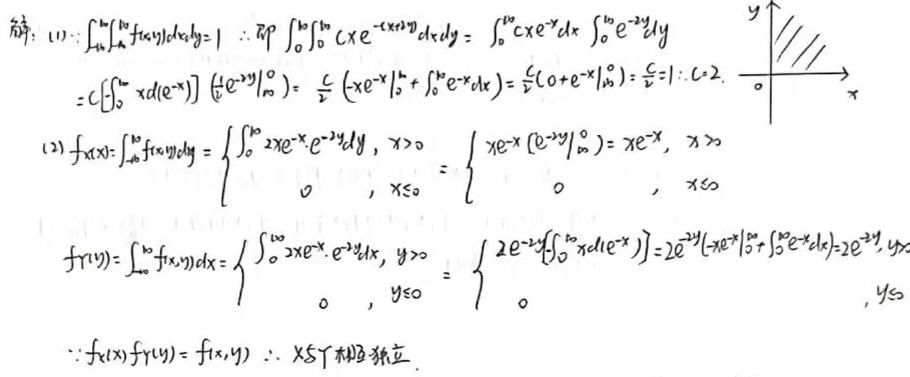1.概率论部分

1 §

设 $X$ 与 $Y$ 相互独立, 且 $X\sim N(2,4),Y\sim N(3,5)$, 求 $X-2Y$ 服从什么分布。

解：

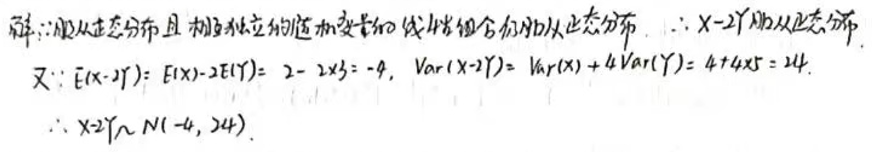
详细解析：

首先，我们已知 $X$ 与 $Y$ 相互独立，并且它们分别服从正态分布 $X\sim N(2,4)$ 和 $Y\sim N(3,5)$。现在我们要求 $X-2Y$ 的分布。

我们知道，如果 $a$ 和 $b$ 是常数，而 $X$ 和 $Y$ 是两个独立的随机变量，那么 $aX+bY$ 也是一个随机变量，并且其期望值和方差可以如下计算：

1. 期望值（均值）：$E(aX+bY)=aE(X)+bE(Y)$
2. 方差：$Var(aX+bY)=a^{2}Var(X)+b^{2}Var(Y)$（因为 $X$ 和 $Y$ 独立）

现在，我们将这些公式应用于 $X-2Y$：

1. 期望值（均值）：

$$E(X-2Y)=E(X)-2E(Y)$$

对于 $X$ 和 $Y$，我们已知 $E(X)=2$ 和 $E(Y)=3$，所以：

$$E(X-2Y)=2-2(3)=2-6=-4$$

2. 方差：

$$Var(X-2Y)=Var(X)+4Var(Y)$$

对于 $X$ 和 $Y$，我们已知 $Var(X)=4$ 和 $Var(Y)=5$，所以：

$$Var(X-2Y)=4+4(5)=4+20=24$$

现在我们已经计算出 $X-2Y$ 的期望值和方差：

$$E(X-2Y)=-4\text{和}Var(X-2Y)=24$$

因此，$X-2Y$ 服从正态分布 $N(-4,24)$，即 $X-2Y\sim N(-4,24)$。这就是 $X-2Y$ 的分布。

---

2 §

设随机变量 $X$ 与 $Y$ 相互独立, 它们的概率分布均为 $B(1,p)$, 求 $P\{X=Y\}$ 。

解：

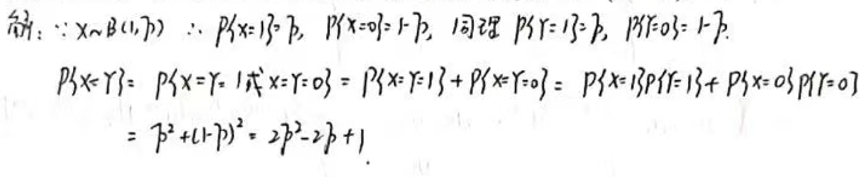
详细解析：

在这个问题中，我们要求两个相互独立的随机变量 $X$ 和 $Y$的相等概率 $P\{X=Y\}$。已知 $X$和 $Y$均服从伯努利分布 $B(1,p)$，即每个随机变量只能取 0 或 1，并且取 1 的概率为 $p$，取 0 的概率为 $1-p$。我们可以通过列出 $X$ 和 $Y$ 的所有可能值来解决此问题。

在伯努利分布中，随机变量的可能值为 0 或 1。因此，$X$ 和 $Y$的所有可能值组合如下：

1. $X=0,Y=0$
2. $X=0,Y=1$
3. $X=1,Y=0$
4. $X=1,Y=1$

我们可以看到，只有在情况 1 和情况 4 中，$X$ 和 $Y$的值相等。

现在我们来计算 $P\{X=Y\}$ 的值。

对于情况 1 $(X=0,Y=0)$，由于$X$ 和 $Y$是相互独立的，所以组合的概率为 $(1-p{)}^2$.

对于情况 4 $(X=1,Y=1)$，由于$X$ 和 $Y$是相互独立的，所以组合的概率为 $p^2$.

因此，$P\{X=Y\}$的值为：

$P\{X=Y\}=(1-p{)}^2+p^2$

现在我们可以化简这个表达式得到最终的答案：

$P\{X=Y\}=(1-p{)}^2+p^2=1-2p+p^2+p^2=2p^2-2p+1$

所以 $P\{X=Y\}=2p^2-2p+1$ 是两个相互独立的伯努利随机变量$X$ 和 $Y$相等的概率。

---

3 §

设随机变量 $(X,Y)$ 的概率密度为 $f(x,y)=\{\begin{array}{ll}cy,& 0<y<x<1,\\ 0,& \text{ 其它. }\end{array}$

(1) 求常数 $c$；

(2) 求 $X$ 与 $Y$ 的边缘密度函数 $f_X(x),f_Y(y)$, 并判断 $X$ 与 $Y$ 是否相互独立；

(3) 求 $P\{X+Y\le 1\}$ 。

（1） §

解：

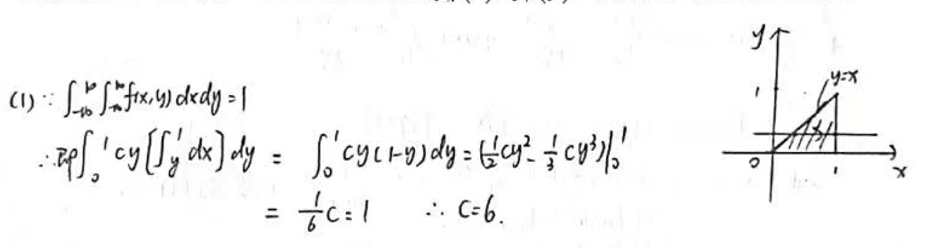
详细解析：

首先，我们按照问题的步骤来解决这个问题。

求常数 c：

概率密度函数必须满足积分等于1的条件。因此，我们需要计算对于给定的概率密度函数 $f(x,y)$ 在定义域内的二重积分，并将其等于1来求解常数 c。在这个情况下，定义域是 $0<y<x<1$。

$$\begin{array}{rl}1& ={\int }_0^1{\int }_0^{x}cydydx\\ & =c{\int }_0^1{\left[\frac{y^2}{2}\right]}_0^{x}dx\\ & =c{\int }_0^1\frac{x^2}{2}dx\\ & =\frac{c}{2}{\left[\frac{x^3}{3}\right]}_0^1\\ & =\frac{c}{2}\left(\frac{1}{3}-0\right)\\ & =\frac{c}{6}\end{array}$$

现在，解出常数 c：

$$\frac{c}{6}=1⟹c=6$$

所以，常数 c 的值为 6。

（2） §

求 $X$ 与 $Y$ 的边缘密度函数 $f_X(x),f_Y(y)$，并判断 $X$ 与 $Y$ 是否相互独立：

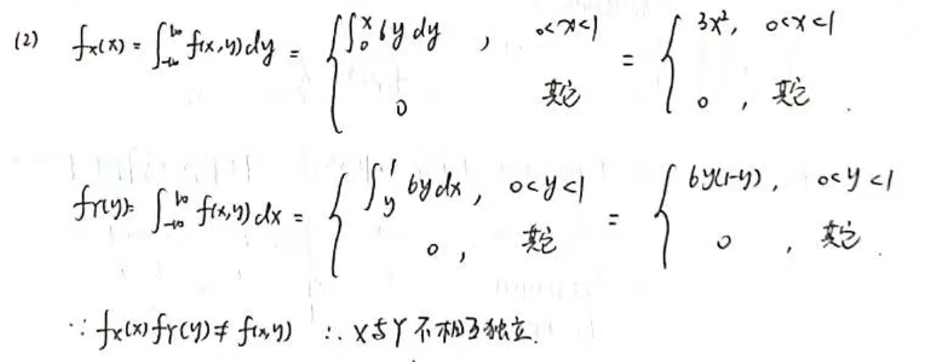
详细解析：

边缘密度函数可以通过将联合密度函数在相应变量的范围内积分来获得。首先，我们来计算 $f_X(x)$：

$$\begin{array}{rl}{f}_X(x)& ={\int }_0^{x}f(x,y)dy\\ & ={\int }_0^{x}6ydy\\ & =6{\int }_0^{x}ydy\\ & =6{\left[\frac{y^2}{2}\right]}_0^x\\ & =6\left(\frac{x^2}{2}-\frac{0^2}{2}\right)\\ & =3x^2\end{array}$$

现在，计算 $f_Y(y)$：

$$\begin{array}{rl}{f}_Y(y)& ={\int }_y^{1}f(x,y)dx\\ & ={\int }_y^{1}6ydx\\ & =6y{\int }_y^{1}dx\\ & =6y{\left[x\right]}_y^1\\ & =6y(1-y)\end{array}$$

现在我们来判断 $X$ 与 $Y$ 是否相互独立。两个随机变量相互独立的充要条件是 $f(x,y)=f_X(x)\cdot f_Y(y)$ 对于所有的 $x$ 和 $y$ 都成立。在我们的情况下：

$$f(x,y)=6y,f_X(x)=3x^2,f_Y(y)=6y(1-y)$$

我们可以看到 $f(x,y)$ 并不等于 $f_X(x)\cdot f_Y(y)$，因此 $X$ 与 $Y$ 不是相互独立的。

（3） §

求 $P\{X+Y\le 1\}$：

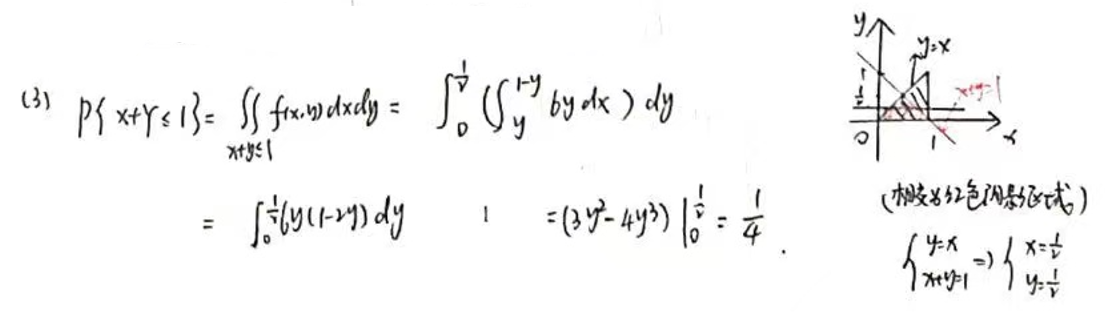
详细解析：

我们要计算 $X+Y\le 1$ 的概率，可以表示为以下积分：

$$P\{X+Y\le 1\}={\iint }_{D}f(x,y)dxdy$$

其中，D 表示满足不等式 $X+Y\le 1$ 的区域。根据给定的概率密度函数 $f(x,y)$，我们可以看出这个区域是 $0<y<x<1$ 和 $x+y\le 1$ 组成的三角形区域。

$$D:\{(x,y)\mid 0<y<x<1,x+y\le 1\}$$

现在，我们可以进行积分计算：

上面是一种解法，先对x进行积分，更直接

也可以先对y进行积分，如下所示，需要两部分

$$\begin{array}{rl}P\{X+Y\le 1\}& ={\iint }_{D}f(x,y)dxdy\\ & ={\int }_0^{\frac{1}{2}}{\int }_0^{x}6ydydx+{\int }_{\frac{1}{2}}^1{\int }_0^{1-x}6ydydx\\ & =\frac{1}{4}\end{array}$$

所以，$P\{X+Y\le 1\}=\frac{1}{4}$。

---

4 §

设二维随机向量 $(X,Y)$ 的联合概率密度函数为 $f(x,y)=\{\begin{array}{cl}cx{e}^{-(x+2y)},& x>0,y>0,\\ 0,& \text{ 其它. }\end{array}$ (1) 求常数 $c$; (2) 求 $X$ 与 $Y$ 的边缘密度函数 $f_X(x),f_Y(y)$, 并判断 $X$ 与 $Y$ 是否相互独立。

5 §

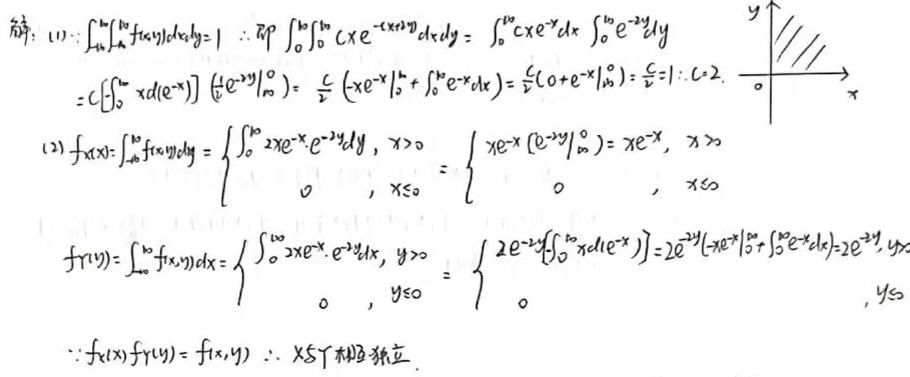
设两个独立的随机变量 $X$ 和 $Y$ 都服从 $[0,1]$ 上的均匀分布, 令 $Z_1=\max (X,Y)$, $Z_2=\min (X,Y)$ 。求: $Z_1$ 和 $Z_2$ 的概率密度函数。

解：

详细解析：

要求出随机变量 $Z_1$ 和 $Z_2$ 的概率密度函数，可以利用累积分布函数（CDF）和概率密度函数（PDF）的性质。

首先，我们知道 $X$ 和 $Y$ 都服从 $[0,1]$ 上的均匀分布，其概率密度函数为 $f_X(x)=f_Y(y)=1$，当 $0\le x\le 1$ 且 $0\le y\le 1$，否则为 $0$。

1. 求 $Z_1$ 的概率密度函数：

$Z_1$ 表示 $X$ 和 $Y$ 中较大的那个值。它的概率密度函数 $f_{Z_1}(z)$ 可以如下求解：

$$\begin{array}{rl}{F}_{Z_1}(z)& =P(Z_1\le z)\\ & =P(\max (X,Y)\le z)\\ & =P(X\le z,Y\le z)\text{(因为 z 是 X 和 Y 中较大的那个)}\\ & =P(X\le z)\cdot P(Y\le z)\text{(由于 X 和 Y 是独立的)}\\ & =F_X(z)\cdot F_Y(z)\text{(CDF 的定义)}\\ & =z\cdot z\text{(因为 X 和 Y 的 CDF 是线性的)}\end{array}$$

其中，$F_X(z)=F_Y(z)=z$，因为 $X$ 和 $Y$ 都是均匀分布，其累积分布函数是 $F_X(z)=F_Y(z)=z$。

接下来，我们可以通过对 $F_{Z_1}(z)$ 求导数来获得 $Z_1$ 的概率密度函数 $f_{Z_1}(z)$：

$$\begin{array}{rl}{f}_{Z_1}(z_1)& =\frac{d}{d{z}_1}{F}_{Z_1}(z_1)\\ & =\frac{d}{d{z}_1}(z_1^2)\\ & =2z_1\end{array}$$

所以，$Z_1$ 的概率密度函数为 $f_{Z_1}(z)=2z$，其中 $0\le z\le 1$。

2. 求 $Z_2$ 的概率密度函数：

$Z_2$ 表示 $X$ 和 $Y$ 中较小的那个值。它的概率密度函数 $f_{Z_2}(z)$ 可以如下求解：

$$\begin{array}{rl}{F}_{Z_2}(z)& =P(Z_2\le z)\\ & =P(\min (X,Y)\le z)\\ & =1-P(\min (X,Y)>z)\\ & =1-P(X>z,Y>z)\text{(用补集法)}\\ & =1-P(X>z)\cdot P(Y>z)\text{(由于 X 和 Y 是独立的)}\\ & =1-(1-F_X(z))\cdot (1-F_Y(z))\\ & =1-(1-z)\cdot (1-z)\\ & =1-(1-z{)}^2\end{array}$$

接下来，我们可以通过对 $F_{Z_2}(z)$ 求导数来获得 $Z_2$ 的概率密度函数 $f_{Z_2}(z)$：

$$\begin{array}{rl}{f}_{Z_2}(z)& =\frac{d}{dz}{F}_{Z_2}(z)\\ & =\frac{d}{dz}\left(1-(1-z{)}^2\right)\\ & =2(1-z)\end{array}$$

所以，$Z_2$ 的概率密度函数为 $f_{Z_2}(z)=2(1-z)$，其中 $0\le z\le 1$。

综上所述，$Z_1$ 的概率密度函数为 $f_{Z_1}(z)=2z$，$Z_2$ 的概率密度函数为 $f_{Z_2}(z)=2(1-z)$，其中 $0\le z\le 1$

注意还有不在$[0,1]$区间的情况，结果都为0