对于一个连续随机变量 $X$ ，其概率密度函数为 $f (x)$ ，其期望值 $E (X)$ 可以通过以下公式计算：

E (X) = \int_{- \infty}^{\infty} x \cdot f (x) d x

对于一个离散随机变量 $X$ ，其概率质量函数为 $p (x)$ ，其期望值 $E (X)$ 可以通过以下公式计算：

E (X) = all x \sum x \cdot p (x)

以下是求期望的步骤：

连续随机变量：
- 将 $x$ 乘以其概率密度函数 $f (x)$ 。
- 对乘积 $x \cdot f (x)$ 在整个实数范围内进行积分。
离散随机变量：
- 将每个可能的 $x$ 值乘以其对应的概率 $p (x)$ 。
- 将所有的乘积求和。

期望值 $E (X)$ 可以被视为随机变量 $X$ 的”平均”或”中心”值，它为我们提供了 $X$ 的一个总体概述。

当然可以。以下是关于期望和方差的详细计算方法：

1. 期望（Expectation）

离散随机变量：对于一个离散随机变量 $X$ ，其概率质量函数为 $p (x)$ ，其期望值 $E (X)$ 定义为：

E (X) = all x \sum x \cdot p (x)

连续随机变量：对于一个连续随机变量 $X$ ，其概率密度函数为 $f (x)$ ，其期望值 $E (X)$ 定义为：

E (X) = \int_{- \infty}^{\infty} x \cdot f (x) d x

2. 方差（Variance）

方差衡量随机变量的取值与其期望值之间的偏离程度。

离散随机变量：对于一个离散随机变量 $X$ ，其方差 $Va r (X)$ 定义为：

Va r (X) = E [(X - E (X))^{2}] = all x \sum (x - E (X))^{2} \cdot p (x)

连续随机变量：对于一个连续随机变量 $X$ ，其方差 $Va r (X)$ 定义为：

Va r (X) = E [(X - E (X))^{2}] = \int_{- \infty}^{\infty} (x - E (X))^{2} \cdot f (x) d x

3. 使用期望计算方差

方差还可以使用期望的性质来更简洁地表示：

Va r (X) = E (X^{2}) - [E (X)]^{2}

其中， $E (X^{2})$ 是 $X$ 的平方的期望值。

4. 标准差（Standard Deviation）

标准差是方差的平方根，表示为：

σ (X) = Va r (X)

标准差提供了一个关于随机变量取值偏离其期望值的平均程度的度量。

这些公式为我们提供了计算期望和方差的基本方法，它们是统计学和概率论中的核心概念，广泛应用于各种分析和建模任务中。

当我们谈论多个样本或多个随机变量时，我们通常关心它们的联合分布、协方差和相关性。以下是关于多个样本或随机变量之间的期望、方差以及其他相关统计量的计算：

期望的性质

方差的性质

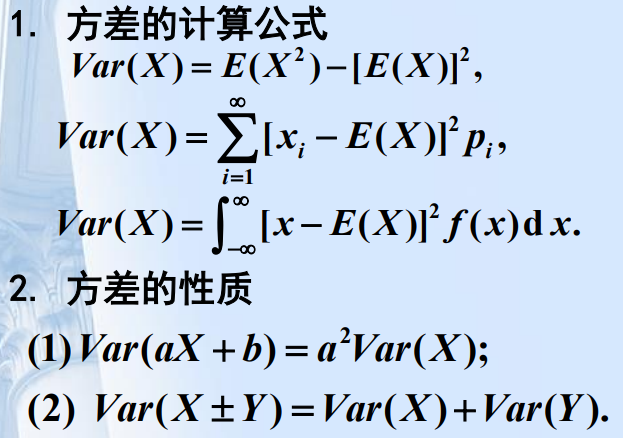
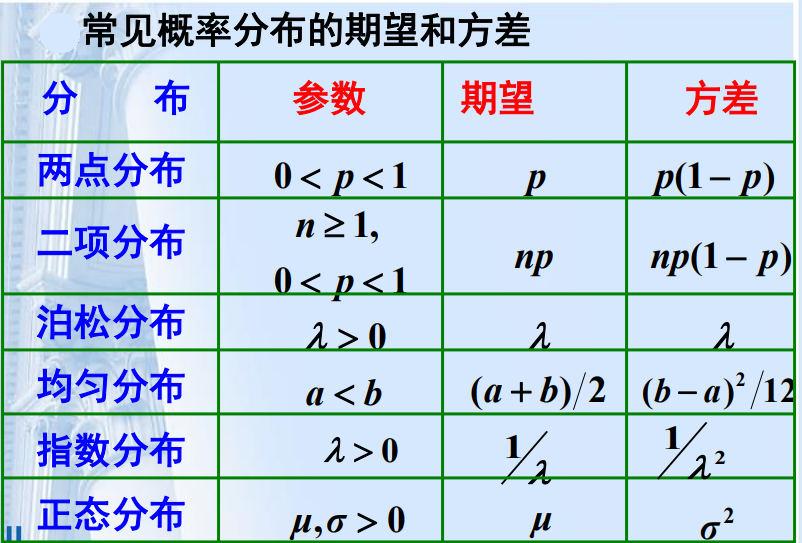
常见概率分布的期望和方差

3. 协方差

协方差衡量两个随机变量之间的线性关系。对于两个随机变量 $X$ 和 $Y$ ，它们的协方差定义为：

C o v (X, Y) = E [(X - E (X)) (Y - E (Y))]

对于样本数据，协方差可以通过以下公式估计：

C o v (X, Y) = \frac{1}{n - 1} i = 1 \sum n (X_{i} - \overset{ˉ}{X}) (Y_{i} - \overset{ˉ}{Y})

其中， $\overset{ˉ}{X}$ 和 $\overset{ˉ}{Y}$ 分别是 $X$ 和 $Y$ 的样本均值。

4. 相关系数

相关系数是两个随机变量线性关系的无量纲度量。对于随机变量 $X$ 和 $Y$ ，它们的皮尔逊相关系数定义为：

ρ (X, Y) = \frac{C o v ( X , Y )}{Va r ( X ) \cdot Va r ( Y )}

对于样本数据，相关系数可以通过以下公式估计：

r (X, Y) = \frac{\sum _{i = 1}^{n} ( X _{i} - X ˉ ) ( Y _{i} - Y ˉ )}{\sum _{i = 1}^{n} ( X _{i} - X ˉ ) ^{2} \cdot \sum _{i = 1}^{n} ( Y _{i} - Y ˉ ) ^{2}}

相关系数的值范围在 $[- 1, 1]$ 之间，其中 1 表示完全正相关，-1 表示完全负相关，0 表示无线性相关。

这些统计量为我们提供了描述和分析多个随机变量或样本之间关系的方法。

当我们考虑两个随机变量 $X$ 和 $Y$ 的线性组合（如相加或相乘）时，我们通常关心这些组合的期望和方差。以下是这些组合的期望和方差的计算方法：

1. 相加

期望：

对于 $Z = X + Y$ ，其期望为：

E (Z) = E (X + Y) = E (X) + E (Y)

方差：

如果 $X$ 和 $Y$ 是独立的，则：

Va r (Z) = Va r (X + Y) = Va r (X) + Va r (Y)

如果 $X$ 和 $Y$ 不是独立的，则：

Va r (Z) = Va r (X) + Va r (Y) + 2 \times C o v (X, Y)

2. 相乘

期望：

对于 $W = X \times Y$ ，其期望为：

E (W) = E (X \times Y)

注意：这不等于 $E (X) \times E (Y)$ ，除非 $X$ 和 $Y$ 是独立的。

方差：

方差的计算较为复杂，特别是当 $X$ 和 $Y$ 不是独立的时候。但是，如果 $X$ 和 $Y$ 是独立的，那么：

Va r (W) = E (X^{2}) E (Y^{2}) + E (X^{2}) [E (Y)]^{2} + [E (X)]^{2} E (Y^{2}) - [E (X)]^{2} [E (Y)]^{2}

这些公式为我们提供了计算随机变量线性组合的期望和方差的方法。当处理更复杂的随机变量组合时，可能需要使用其他技术或工具来帮助计算。

对于随机变量的线性组合 $Z = X - 2 Y$ ，我们可以使用以下公式来计算其方差：

$Va r (Z) = Va r (X - 2 Y)$

使用方差的性质，我们有：

$Va r (X - 2 Y) = Va r (X) + 4 \times Va r (Y) - 2 \times 2 \times C o v (X, Y)$

其中：

$Va r (X)$ 是 $X$ 的方差。
$Va r (Y)$ 是 $Y$ 的方差。
$C o v (X, Y)$ 是 $X$ 和 $Y$ 之间的协方差。

具体地：

$Va r (X)$ 是 $X$ 的方差。
$4 \times Va r (Y)$ 是 $2 Y$ 的方差。因为方差的性质是 $Va r (c Y) = c^{2} \times Va r (Y)$ ，其中 $c$ 是常数。
$- 2 \times 2 \times C o v (X, Y)$ 是 $X$ 和 $2 Y$ 之间的协方差。因为协方差的性质是 $C o v (X, c Y) = c \times C o v (X, Y)$ 。

将这三个部分相加，我们得到 $Z = X - 2 Y$ 的方差。

期望的线性性质

期望的线性性质是期望运算的一个非常重要和基本的性质。它描述了随机变量和常数的线性组合的期望与这些随机变量和常数的期望的线性组合之间的关系。

具体来说，期望的线性性质可以表述为：

对于任意常数 $a$ 和 $b$ 以及随机变量 $X$ 和 $Y$ ，有： $E (a X + bY) = a E (X) + b E (Y)$
更一般地，对于任意常数 $a_{1}, a_{2}, \dots, a_{n}$ 和随机变量 $X_{1}, X_{2}, \dots, X_{n}$ ，有： $E (\sum_{i = 1}^{n} a_{i} X_{i}) = \sum_{i = 1}^{n} a_{i} E (X_{i})$

这些性质意味着，当我们要计算多个随机变量的线性组合的期望时，我们可以单独计算每个随机变量的期望，然后将它们组合起来。

需要注意的是，虽然期望具有线性性质，但方差不具有这种性质。例如， $Va r (a X + bY)$ 不能简单地表示为 $a^{2} Va r (X) + b^{2} Va r (Y)$ ，除非 $X$ 和 $Y$ 是独立的。

方差的性质

方差具有以下性质：

1. 非负性

对于任何随机变量 $X$ ，其方差始终是非负的： $Va r (X) \geq 0$

2. 常数的方差

对于任何常数 $c$ ，其方差为零： $Va r (c) = 0$

3. 方差的尺度性质

对于任何常数 $a$ 和随机变量 $X$ ，有： $Va r (a X) = a^{2} Va r (X)$

4. 独立随机变量的方差之和

如果 $X$ 和 $Y$ 是独立的随机变量，那么： $Va r (X + Y) = Va r (X) + Va r (Y)$ $Va r (X - Y) = Va r (X) + Va r (Y)$

5. 两个随机变量的方差之和

对于任何两个随机变量 $X$ 和 $Y$ ，有： $Va r (X + Y) = Va r (X) + Va r (Y) + 2 C o v (X, Y)$ $Va r (X - Y) = Va r (X) + Va r (Y) - 2 C o v (X, Y)$ 其中 $C o v (X, Y)$ 是 $X$ 和 $Y$ 之间的协方差。

6. 线性组合的方差

对于任意常数 $a$ 和 $b$ 以及随机变量 $X$ 和 $Y$ ，有： $Va r (a X + bY) = a^{2} Va r (X) + b^{2} Va r (Y) + 2 ab C o v (X, Y)$

这些性质为我们提供了计算和理解方差的工具。特别是，它们帮助我们理解方差如何随随机变量的线性变换而变化，以及如何计算多个随机变量的组合的方差。

概率论与数理统计——笔记

目录

目录

期望、方差