矩估计

矩估计法是统计学中的一种参数估计方法。它的基本思想是利用样本矩与总体矩之间的关系来估计总体参数。具体来说，矩估计法是通过使样本矩等于相应的总体矩来得到参数的估计值。

以下是矩估计法的基本步骤：

1. 定义总体矩：

   • $k$ 阶总体矩定义为 $E(X^k)$，其中 $E$ 表示期望值，$X$ 是随机变量。

2. 计算样本矩：

   • $k$ 阶样本矩定义为 $\frac{1}{n}{\sum }_{i=1}^n{X}_i^k$，其中 $X_i$ 是样本中的第 $i$ 个观测值，$n$ 是样本大小。

3. 建立方程：

   • 为了估计参数，我们将样本矩设为相应的总体矩，从而得到一个或多个方程。

4. 求解方程：

   • 通过解上述方程，我们可以得到参数的矩估计值。

例如，考虑正态分布，它有两个参数：均值 $\mu$ 和方差 ${\sigma }^2$。我们可以使用矩估计法来估计这两个参数。具体来说，我们可以将样本均值设为总体均值，将样本方差设为总体方差，然后解这两个方程来得到 $\mu$ 和 ${\sigma }^2$ 的估计值。

矩估计法的一个优点是它的计算通常比较简单。然而，这种方法得到的估计值不一定是最优的，特别是在小样本情况下。因此，在实际应用中，矩估计法可能不如其他方法（如最大似然估计）受到青睐。

“矩”是什么？ §

在统计学和概率论中，“矩”（Moment）是一个描述随机变量或概率分布特性的重要概念。矩可以帮助我们了解分布的形状、中心位置和分散程度等特性。

矩主要有以下几种：

1. 原点矩（Raw Moment）：

   • 对于随机变量 $X$，其 $k$ 阶原点矩定义为 $E(X^k)$，其中 $E$ 表示期望值。特别地，一阶原点矩就是随机变量的期望值，即 $E(X)$。

2. 中心矩（Central Moment）：

   • 对于随机变量 $X$，其 $k$ 阶中心矩定义为 $E[(X-\mu {)}^k]$，其中 $\mu$ 是 $X$ 的期望值。特别地，二阶中心矩就是随机变量的方差，即 $E[(X-\mu {)}^2]$。

以下是一些常见的矩及其意义：

• 一阶原点矩：随机变量的期望值。
• 二阶原点矩：随机变量的平方的期望值。
• 二阶中心矩：随机变量的方差，描述了数据的分散程度。
• 三阶中心矩：与数据的偏度（Skewness）有关，描述了数据分布的不对称性。
• 四阶中心矩：与数据的峰度（Kurtosis）有关，描述了数据分布的尖锐或扁平程度。

矩在统计学中有广泛的应用，它们为我们提供了描述和分析数据分布的有力工具。

以下是上述提到的各种矩的图像：

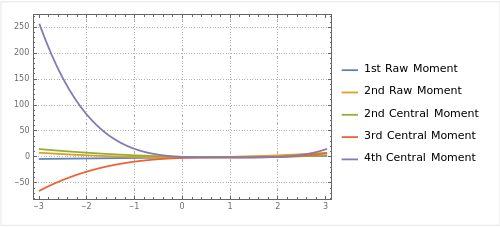
图中展示了：

• 1st Raw Moment：$y=x$
• 2nd Raw Moment：$y=x^2$
• 2nd Central Moment：$y=(x-1{)}^2$
• 3rd Central Moment：$y=(x-1{)}^3$
• 4th Central Moment：$y=(x-1{)}^4$

请注意，这些图像只是为了直观地展示各种矩的形状，并不代表实际的概率分布或数据分布。

为什么叫“矩” §

“矩”（Moment）在物理学中原本是描述物体关于某一点或某一轴的转动效果的量，例如力矩或转动矩。在数学和统计学中，“矩”这个词被借用来描述函数或概率分布的某些特性。

在统计学中，矩的概念与物理中的矩有相似之处。考虑物理中的力矩，它是力与其臂长（到旋转轴的距离）的乘积。在统计学中，随机变量的矩可以看作是数据值与其权重（概率）的乘积，然后对所有可能的数据值求和或积分。

因此，从直观上讲，统计中的矩与物理中的矩都涉及到某种”乘积”或”加权”的概念。这种相似性可能是为什么统计学中采用了”矩”这个词来描述这一概念的原因。

至于中文中为什么将”Moment”翻译为”矩”，这可能是因为早期的学者在引入这一概念时，为了保持与物理学中的术语一致性，选择了”矩”这个词。随着时间的推移，这种翻译在学术界得到了普遍接受，并成为了标准术语。