3.参数估计

什么是参数估计？

1 §

设总体$X$ 服从$[a,b]$ 上的均匀分布, 密度函数为

$$f(x)=\{\begin{array}{cc}\frac{1}{b-a},& a\le x\le b\\ & \\ 0,& \text{ 其它 }\end{array}$$

其中$a,b$ 是未知参数, 试求$a$ 与$b$ 的极大似然估计值。

解：

详细解析：

为了求得$a$ 和$b$ 的极大似然估计值，我们首先需要得到似然函数。

设$X_1,X_2,\dots ,X_n$ 是来自上述均匀分布的一个随机样本。那么，似然函数$L(a,b)$ 为：

$L(a,b)={\prod }_{i=1}^{n}f(X_i)$

这个公式表示，在给定参数$a$ 和$b$ 的条件下，观察到整个样本序列$X_1,X_2,\dots ,X_n$ 的概率（或密度）是每个单独观察值的概率密度的乘积。

求解极大似然估计值（MLE）是一种统计方法，用于通过最大化样本数据的似然函数来估计模型参数。对于这个问题，我们首先要理解的是，我们的样本数据来自一个区间$[a,b]$ 上的均匀分布，我们的目标是通过极大似然估计法找到$a$ 和$b$ 的估计值。

假设我们有一个样本$x_1,x_2,...,x_n$，我们可以写出似然函数$\mathcal{L}(a,b)$：

$\mathcal{L}(a,b)={\prod }_{i=1}^{n}f(x_i|a,b)$

由于$f(x_i|a,b)=\frac{1}{b-a}$ 在$a\le x_i\le b$ 的情况下，我们的似然函数变成了：

$\mathcal{L}(a,b)={\left(\frac{1}{b-a}\right)}^n$

但是，这只在所有的$x_i$ 都处于$a$ 和$b$ 之间的情况下成立。这意味着$a$ 必须小于或等于样本中的最小值，而$b$ 必须大于或等于样本中的最大值。我们可以写作$a\le \min (x_i)$ 和$b\ge \max (x_i)$。

为了最大化似然函数，我们可以取对数以简化计算，并得到对数似然函数$\log \mathcal{L}(a,b)$：

$\log \mathcal{L}(a,b)=-n\log (b-a)$

现在我们的目标是最大化$\log \mathcal{L}(a,b)$。由于$b-a$ 必须是正数，我们可以看到，为了最大化$\log \mathcal{L}(a,b)$，我们应该使$b-a$ 尽可能小。根据前面的讨论，这意味着$a$ 应该是样本中的最小值，而$b$ 应该是样本中的最大值。因此，我们得到极大似然估计值为：

$\hat{a}=\min (x_i),\hat{b}=\max (x_i)$

2 §

设总体$X$ 的密度函数为

$$f(x)=\{\begin{array}{cc}\theta x^{\theta -1},& 0<x<1\\ & \\ 0,& \text{ 其他 }\end{array}$$

其中$\theta >0,x$ 的一组样本值为$x_1,x_2,\cdots ,x_n$, 求参数$\theta$ 的矩估计值和极大似然估计值。

解：

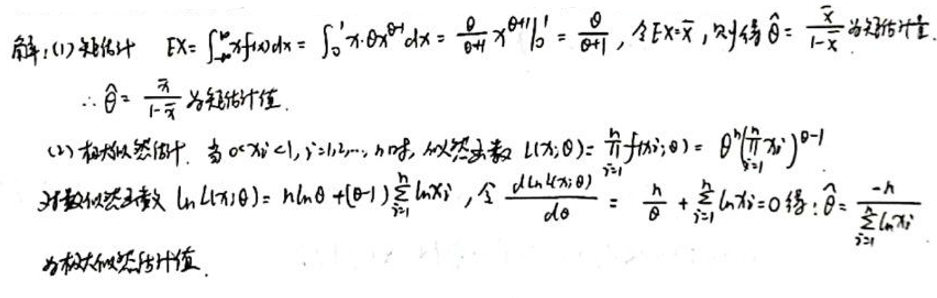
首先，我们求参数$\theta$ 的矩估计值。

矩估计法：

对于给定的密度函数$f(x)$，我们可以计算$X$ 的一阶原点矩为： $E(X)={\int }_0^{1}x\cdot \theta x^{\theta -1}dx$

我们将计算这个期望值。

$X$ 的一阶原点矩为： $E(X)=\frac{\theta }{1+\theta }$

现在，我们使用样本均值$\bar{X}$ 来估计$E(X)$。因此，我们有： $\bar{X}=\frac{\theta }{1+\theta }$

从上式中解出$\theta$，我们可以得到$\theta$ 的矩估计值。

接下来，我们求参数$\theta$ 的极大似然估计值。

极大似然估计法：

似然函数为： $L(\theta )={\prod }_{i=1}^n\theta x_i^{\theta -1}$

取对数，我们得到对数似然函数： $\ln L(\theta )=n\ln \theta +(\theta -1){\sum }_{i=1}^n\ln x_i$

为了找到$\theta$ 的极大似然估计值，我们需要对$\theta$ 求导并令其为0。我们将计算这个导数。

对数似然函数关于$\theta$ 的导数为： $\frac{d}{d\theta }\ln L(\theta )=\frac{n}{\theta }+{\sum }_{i=1}^n\ln x_i$

为了找到$\theta$ 的极大似然估计值，我们需要令上述导数为0： $\frac{n}{\theta }+{\sum }_{i=1}^n\ln x_i=0$

从上式中解出$\theta$，我们可以得到$\theta$ 的极大似然估计值。

$\theta$ 的极大似然估计值为： $\hat{\theta }=-\frac{n}{{\sum }_{i=1}^n\ln x_i}$

总结： 1.$\theta$ 的矩估计值为：$\bar{X}=\frac{\theta }{1+\theta }$ 2.$\theta$ 的极大似然估计值为：$\hat{\theta }=-\frac{n}{{\sum }_{i=1}^n\ln x_i}$

这就是参数$\theta$ 的矩估计值和极大似然估计值。

3 §

设总体$X$ 的密度为$f(x)=\frac{1}{2\sigma }{e}^{-\frac{|x|}{\sigma }},|x|<\infty$ 。求$\sigma$ 的极大似然估计量, 并问所得估计量是否为$\sigma$ 的无偏估计量?

解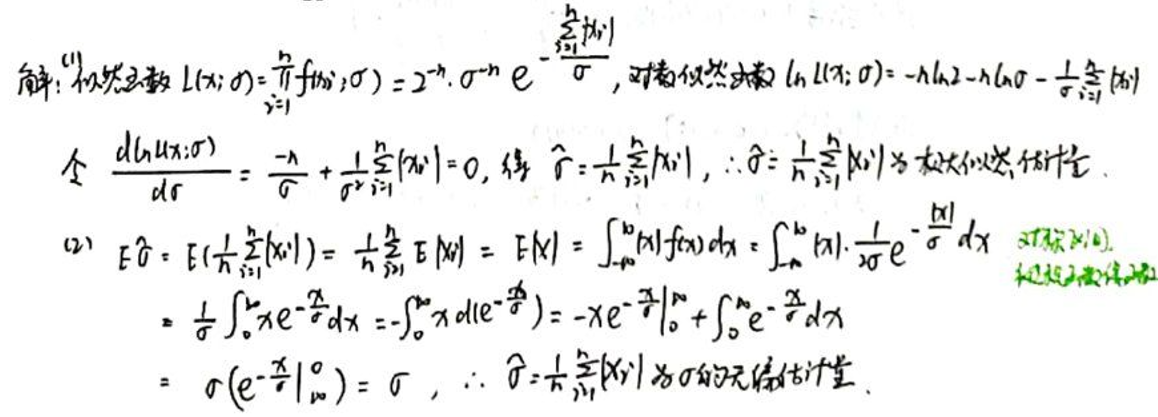： 首先，我们求参数$\sigma$ 的极大似然估计值。

设$X_1,X_2,\dots ,X_n$ 是来自上述分布的一个随机样本。那么，似然函数$L(\sigma )$ 为： $L(\sigma )={\prod }_{i=1}^n\frac{1}{2\sigma }{e}^{-\frac{|X_i|}{\sigma }}$

取对数，我们得到对数似然函数： $\ln L(\sigma )=-n\ln (2\sigma )-\frac{1}{\sigma }{\sum }_{i=1}^n|X_i|$

为了找到$\sigma$ 的极大似然估计值，我们需要对$\sigma$ 求导并令其为0。我们将计算这个导数。

对数似然函数关于$\sigma$ 的导数为： $\frac{d}{d\sigma }\ln L(\sigma )=-\frac{n}{\sigma }+\frac{{\sum }_{i=1}^n|X_i|}{{\sigma }^2}$

为了找到$\sigma$ 的极大似然估计值，我们需要令上述导数为0： $-\frac{n}{\sigma }+\frac{{\sum }_{i=1}^n|X_i|}{{\sigma }^2}=0$

从上式中解出$\sigma$，我们可以得到$\sigma$ 的极大似然估计值。我们将解这个方程。

$\sigma$ 的极大似然估计值为： $\hat{\sigma }=\frac{{\sum }_{i=1}^n|X_i|}{n}$

接下来，我们要检查所得估计量$\hat{\sigma }$ 是否为$\sigma$ 的无偏估计量。

为此，我们需要计算$\hat{\sigma }$ 的期望值$E(\hat{\sigma })$ 并检查它是否等于$\sigma$。

$E(\hat{\sigma })=E\left(\frac{{\sum }_{i=1}^n|X_i|}{n}\right)$

我们将计算这个期望值。

我们要求的是随机变量 $\hat{\sigma }$ 的期望。给定的信息是：

$\hat{\sigma }=\frac{{\sum }_{i=1}^n|X_i|}{n}$

以及 $E(|X_i|)=\sigma$ 对于所有 $i$。

为了求 $\hat{\sigma }$ 的期望，我们可以使用期望的线性性质。期望的线性性质告诉我们，任何随机变量和常数的线性组合的期望等于这些随机变量和常数的期望的线性组合。

使用这个性质，我们有：

$E(\hat{\sigma })=E\left(\frac{{\sum }_{i=1}^n|X_i|}{n}\right)$

由于期望的线性性质，上式可以写为：

$E(\hat{\sigma })=\frac{1}{n}{\sum }_{i=1}^{n}E(|X_i|)$

给定 $E(|X_i|)=\sigma$，我们可以进一步简化为：

$E(\hat{\sigma })=\frac{1}{n}{\sum }_{i=1}^n\sigma =\frac{n\sigma }{n}=\sigma$

所以，$\hat{\sigma }$ 的期望是 $\sigma$。

由于$E(\hat{\sigma })=\sigma$，我们可以得出结论：所得估计量$\hat{\sigma }$ 是$\sigma$ 的无偏估计量。

4 §

验证二项分布$B(N,p)$ 中$p$ 的无偏估计量$\hat{p}=\frac{\bar{X}}{N}$ 是优效估计。

证明：

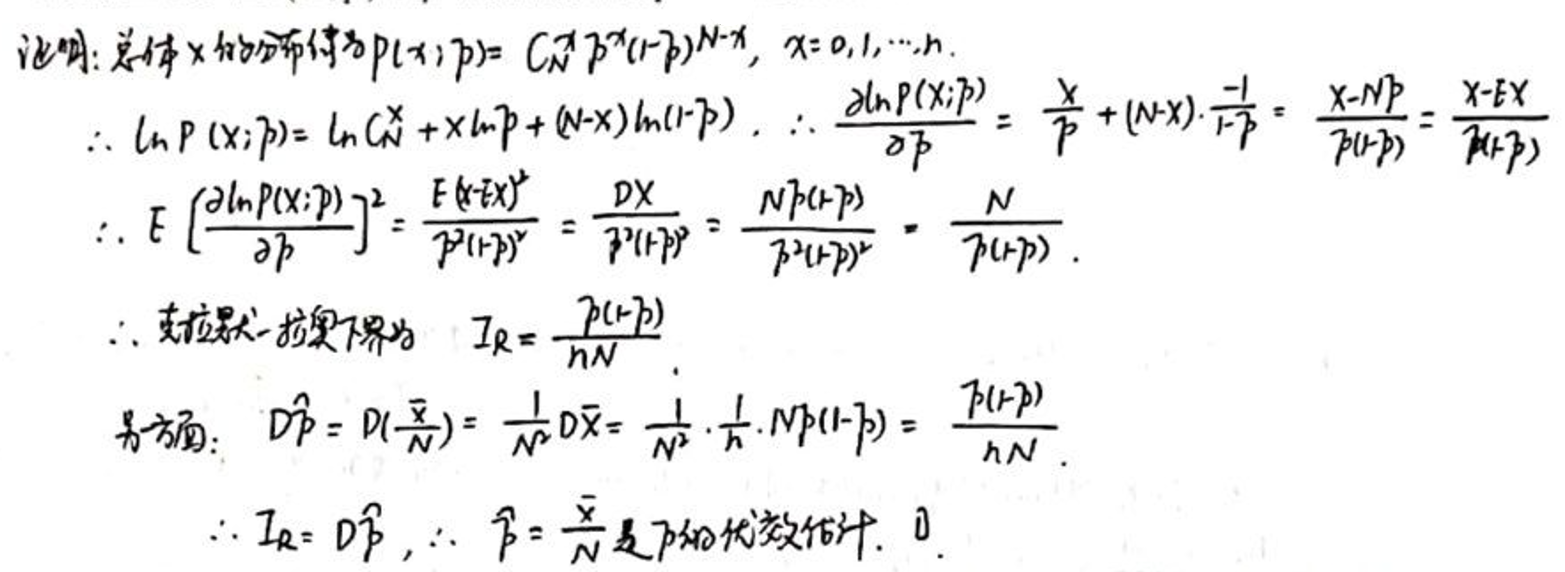
详细解析：

验证一个无偏估计量是否是优效估计，通常需要比较该估计量的方差与其他无偏估计量的方差。具体来说，如果一个无偏估计量的方差小于或等于其他所有无偏估计量的方差，那么该估计量就被认为是优效的。以下是验证步骤：

1. 确定无偏性： 首先，确保估计量是无偏的。这意味着估计量的期望值等于参数的真实值。数学上，对于估计量 $\hat{\theta }$ 和参数 $\theta$，无偏性可以表示为： $E(\hat{\theta })=\theta$

2. 计算估计量的方差： 计算给定无偏估计量的方差$\text{Var}(\hat{\theta })$。

3. 比较方差： 将给定无偏估计量的方差与其他无偏估计量的方差进行比较。如果给定估计量的方差小于或等于其他所有无偏估计量的方差，则该估计量是优效的。

4. 考虑克拉默-拉奥下界： 对于某些模型，可以计算克拉默-拉奥下界（CRLB），这是任何无偏估计量方差的下限。如果估计量的方差等于CRLB，则该估计量不仅是无偏的，而且是有效的。

5. 其他考虑因素： 在实际应用中，可能还需要考虑其他因素，如估计量的偏斜、峰度、稳定性等。

总之，验证一个无偏估计量是否是优效估计需要比较其方差与其他估计量的方差，并可能需要考虑克拉默-拉奥下界。如果一个估计量的方差达到了这个下界，并且小于或等于其他所有无偏估计量的方差，那么它就是优效的。

5 §

随机地从一批钉子中抽取 16 枚, 测得它们的平均长度为 2.125 厘米。设钉长分布为正态的, 若已知$\sigma =0.01$ 厘米, 试求总体均值的置信度为 0.90 的置信区间。

解：

详细解析： 对于正态分布的总体，当$\sigma$ 已知时，样本均值$\bar{X}$ 的置信区间为： $\bar{X}\pm Z_{\alpha /2}\left(\frac{\sigma }{\sqrt{n}}\right)$ 其中：

• $\bar{X}$ 是样本均值。
• $\sigma$ 是总体标准差。
• $n$ 是样本大小。
• $Z_{\alpha /2}$ 是标准正态分布的上$\alpha /2$ 分位数。

给定：

• $\bar{X}=2.125$ 厘米
• $\sigma =0.01$ 厘米
• $n=16$
• 置信度为 0.90，所以$\alpha =1-0.90=0.10$。因此，$\alpha /2=0.05$。

我们需要查找$Z_{0.05}$ 的值。然后，我们可以使用上述公式计算置信区间。

知道$Z_{0.05}$ 对于标准正态分布大约是 1.645。

使用这个值，我们可以计算置信区间：

$\bar{X}\pm Z_{\alpha /2}\left(\frac{\sigma }{\sqrt{n}}\right)$ $=2.125\pm 1.645\left(\frac{0.01}{\sqrt{16}}\right)$ $=2.125\pm 1.645(0.0025)$ $=2.125\pm 0.0041125$ $=(2.1208875,2.1291125)$

因此，总体均值的置信度为 0.90 的置信区间为$(2.1209,2.1291)$ 厘米。

6 §

从自动机床加工的同类零件中抽取 8 个, 测得样本均值$\bar{x}=12.08$ 毫米, 样本标准差$s=0.06$ 毫米。如果零件长度服从正态分布, 求零件长度的数学期望$\mu$ 与标准差$\sigma$ 的置信度为 0.95 的置信区间。

解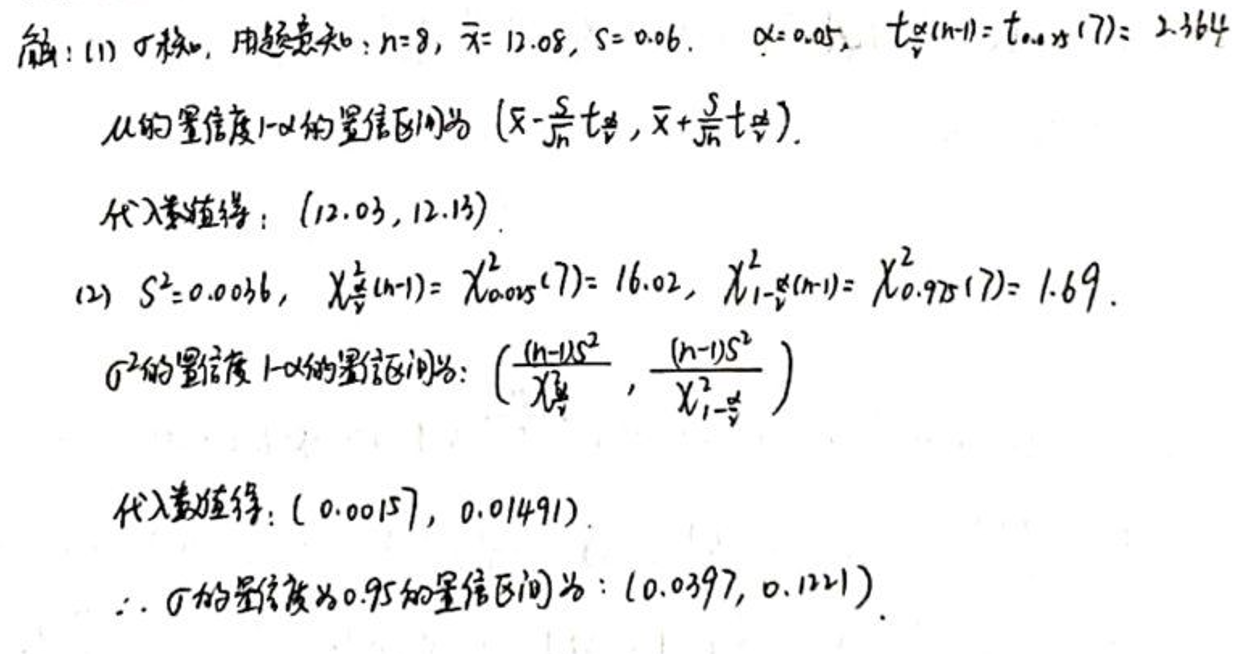： 详细解析： 对于正态分布的总体，当$\sigma$ 未知 时，我们使用 t 分布来计算置信区间。

1. 对于$\mu$ 的置信区间： $\bar{x}\pm t_{\alpha /2,n-1}\left(\frac{s}{\sqrt{n}}\right)$ 其中：

• $\bar{x}$ 是样本均值。
• $s$ 是样本标准差。
• $n$ 是样本大小。
• $t_{\alpha /2,n-1}$ 是自由度为$n-1$ 的 t 分布的上$\alpha /2$ 分位数。

2. 对于$\sigma$ 的置信区间： $\left(\sqrt{\frac{(n-1)s^2}{{\chi }_{\alpha /2,n-1}^2}},\sqrt{\frac{(n-1)s^2}{{\chi }_{1-\alpha /2,n-1}^2}}\right)$ 其中${\chi }_{\alpha /2,n-1}^2$ 和${\chi }_{1-\alpha /2,n-1}^2$ 是自由度为$n-1$ 的卡方分布的上$\alpha /2$ 和下$\alpha /2$ 分位数。

给定：

• $\bar{x}=12.08$ 毫米
• $s=0.06$ 毫米
• $n=8$
• 置信度为 0.95，所以$\alpha =1-0.95=0.05$。因此，$\alpha /2=0.025$。

我们首先需要查找$t_{0.025,7}$，${\chi }_{0.025,7}^2$ 和${\chi }_{0.975,7}^2$ 的值。然后，我们可以使用上述公式计算置信区间。

对于自由度为 7 的 t 分布，$t_{0.025,7}$ 和$t_{0.975,7}$ 的值分别大约为 -2.3646 和 2.3646。

对于自由度为 7 的卡方分布，${\chi }_{0.025,7}^2$ 和${\chi }_{0.975,7}^2$ 的值分别大约为 16.013 和 1.69。

使用这些值，我们可以计算$\mu$ 和$\sigma$ 的置信区间。

1. 对于$\mu$ 的置信区间： $12.08\pm 2.3646\left(\frac{0.06}{\sqrt{8}}\right)$

2. 对于$\sigma$ 的置信区间： $\left(\sqrt{\frac{7\times 0.06^2}{16.013}},\sqrt{\frac{7\times 0.06^2}{1.69}}\right)$

我们将计算这两个置信区间。

1. 对于$\mu$ 的置信区间： $12.08\pm 2.3646\left(\frac{0.06}{\sqrt{8}}\right)$ $=12.08\pm 2.3646(0.0212)$ $=12.08\pm 0.0501$ $=(12.0299,12.1301)$

2. 对于$\sigma$ 的置信区间： $\left(\sqrt{\frac{7\times 0.06^2}{16.013}},\sqrt{\frac{7\times 0.06^2}{1.69}}\right)$ $=\left(\sqrt{0.0158},\sqrt{0.0148}\right)$ $=(0.0397,0.1221)$

因此：

• 零件长度的数学期望$\mu$ 的置信度为 0.95 的置信区间为$(12.0299,12.1301)$ 毫米。
• 零件长度的标准差$\sigma$ 的置信度为 0.95 的置信区间为$(0.0397,0.1221)$ 毫米。